gkt-horizontal-line
<1年p.227>
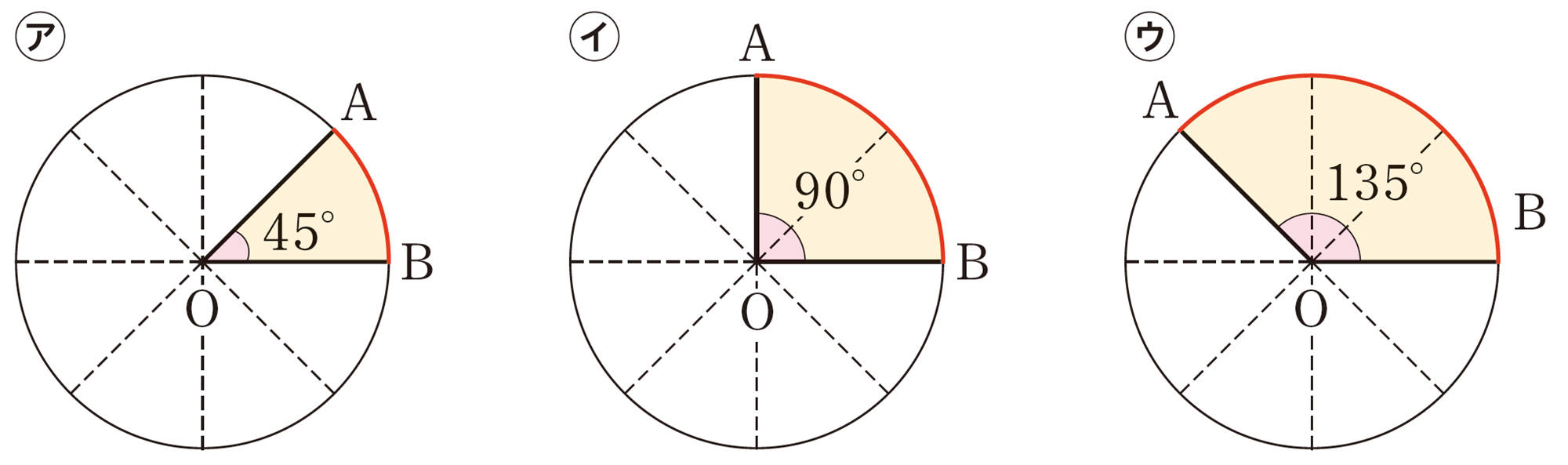
円錐の表面積を求めるために，おうぎ形の面積について調べてみよう。
例 ３ 次の図のように，おうぎ形の半径を変えずに，中心角を2倍，3倍，…にしていくと，弧の長さも，面積も2倍，3倍，…になる。
例3から，次のことがわかる。
1つの円では，おうぎ形の弧の長さは中心角の大きさに比例する。
おうぎ形の面積は中心角の大きさに比例する。
問 ６ 1 つの円で，おうぎ形の面積は弧の長さに比例するといえますか。
問 ７ 半径6 cm，中心角[mathjax]\(120^{\circ}\)のおうぎ形について，次の問いに答えなさい。
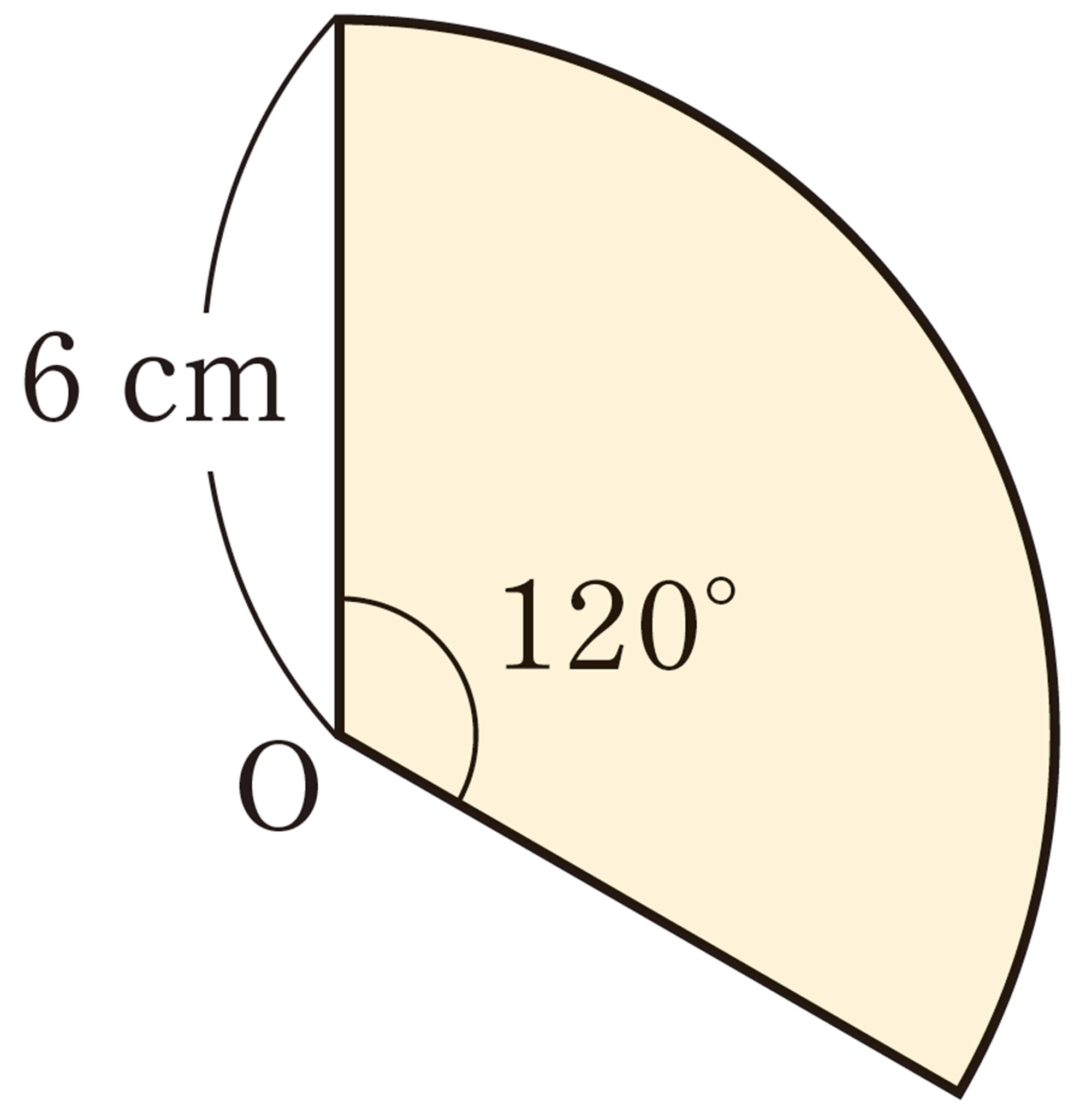
⑴ このおうぎ形の面積は，同じ半径の円の面積の何倍ですか。
⑵ 面積を求めなさい。
⑶ 弧の長さを求めなさい。
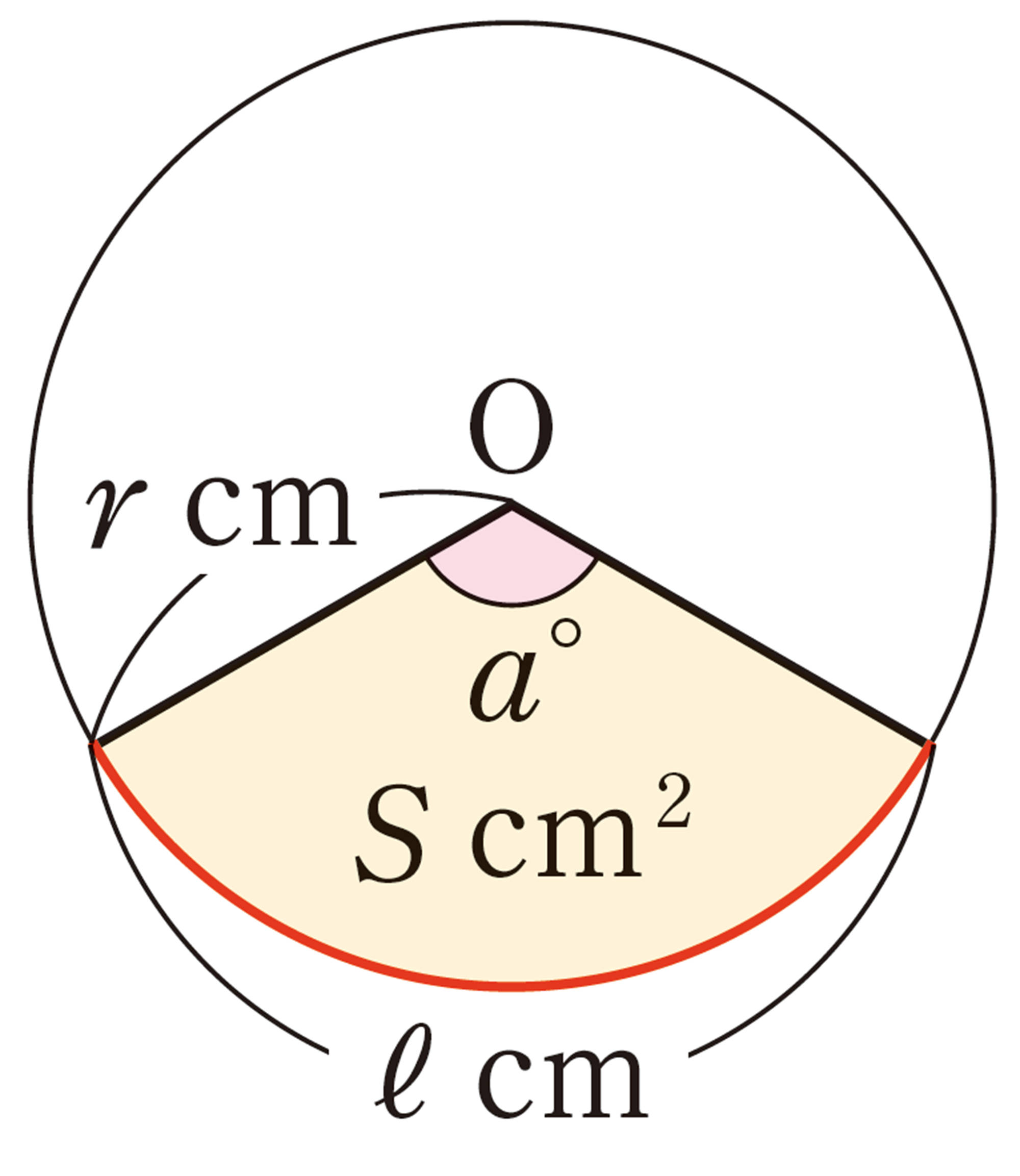
おうぎ形の弧の長さと面積は，次の式で求めることができる。
おうぎ形の弧の長さと面積
半径r cm，中心角[mathjax]\(a^{\circ}\)のおうぎ形の弧の長さを ℓ cm，面積をS cm²とすると，
[mathjax] \(ℓ=2\pi r\times \dfrac{a}{360}\)，[mathjax] \(S=\pi r^{2}\times \dfrac{a}{360}\)
問 ８ 半径4cm，中心角[mathjax]\(135^{\circ}\)のおうぎ形の弧の長さと面積を求めなさい。
