<1年p.223>
２節 立体の表面積・体積
表面の面積や体積の関係は？
古代ギリシャの数学者であるアルキメデス(紀元前287頃〜紀元前212)は，球の体積が，それがぴったり入る円柱の体積の[mathjax] \( \dfrac{2}{3}\)に等しいことを発見し，自分の墓石に，右の図のような図形をかかせたといわれています。このような関係にある立体について考えてみましょう。
【１】 右のような3つの立体があります。
㋐ 底面の半径が5 cm，高さが10 cmの円錐
㋑ 半径5 cmの球
㋒ 底面の半径が5 cm，高さが10 cmの円柱
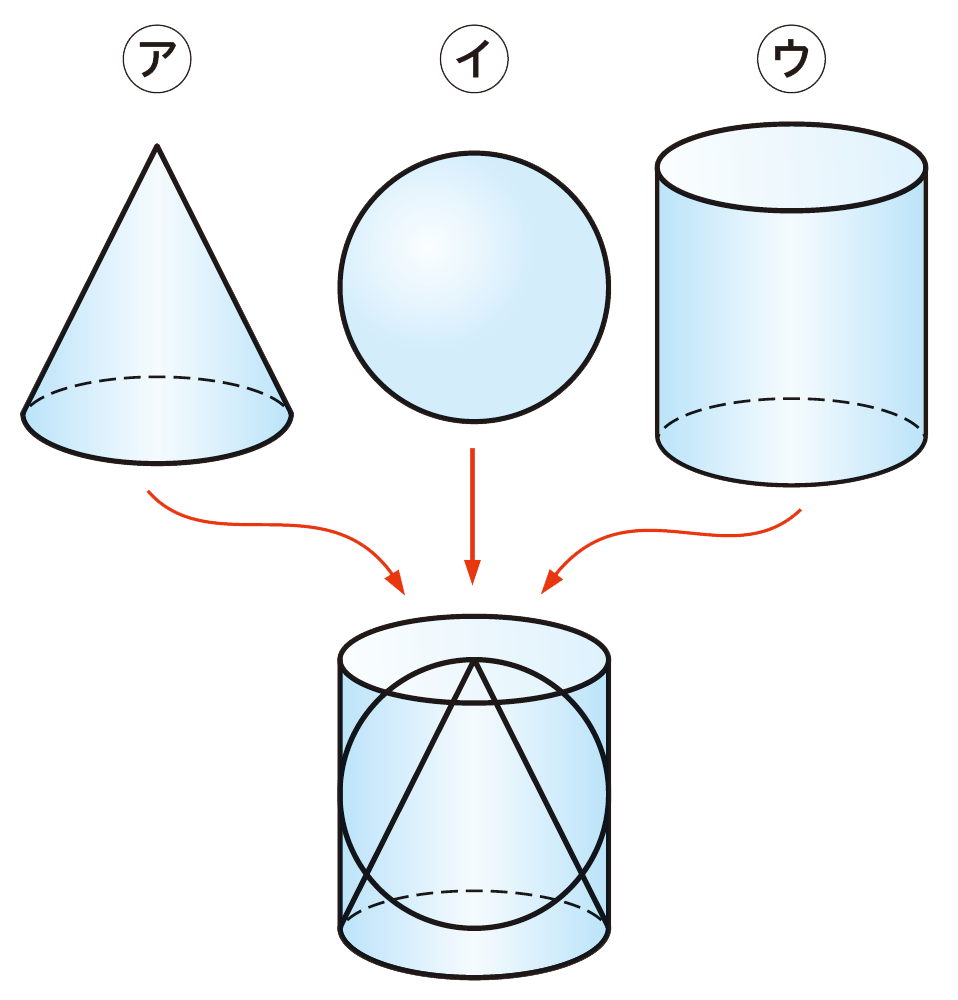
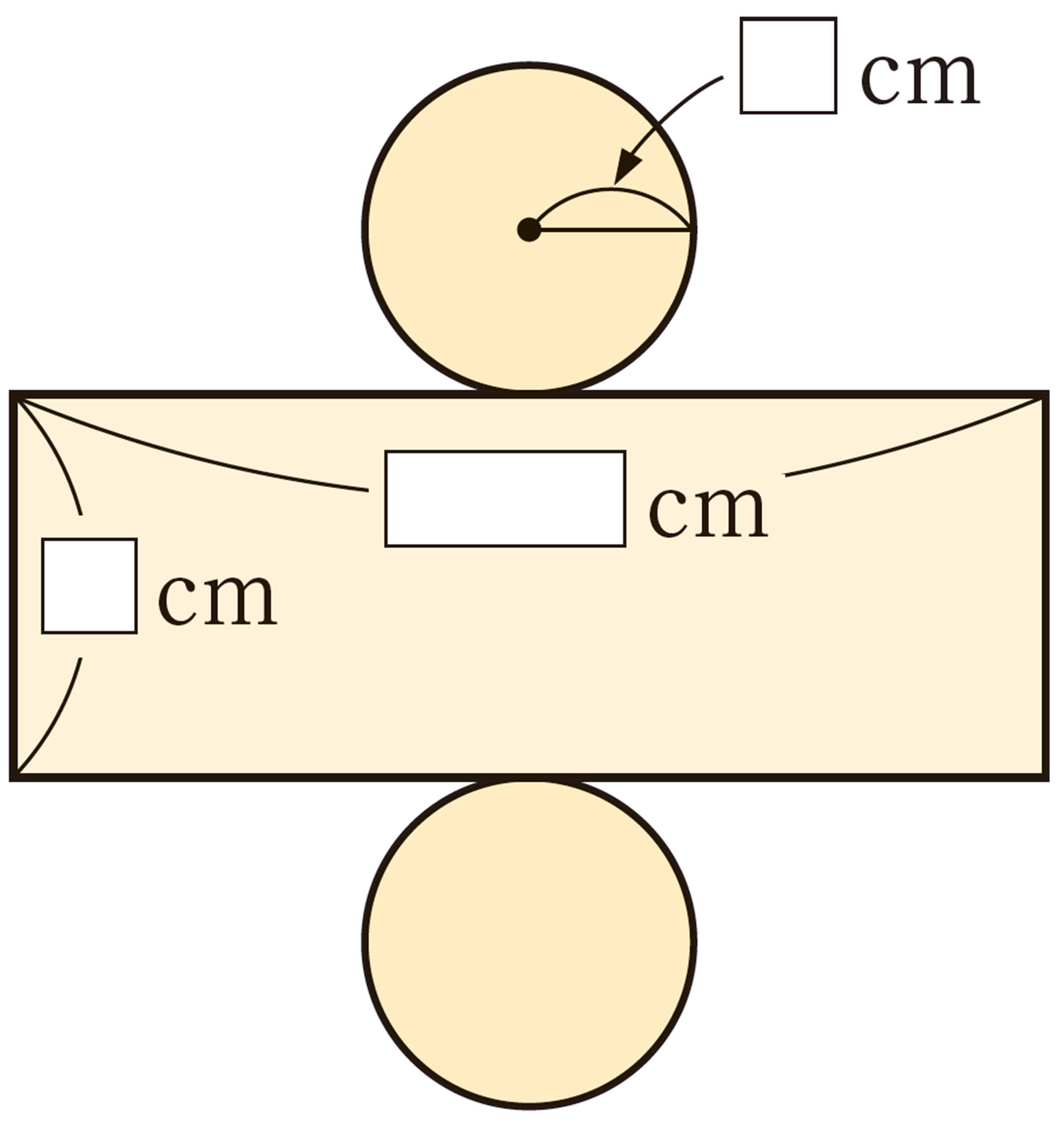
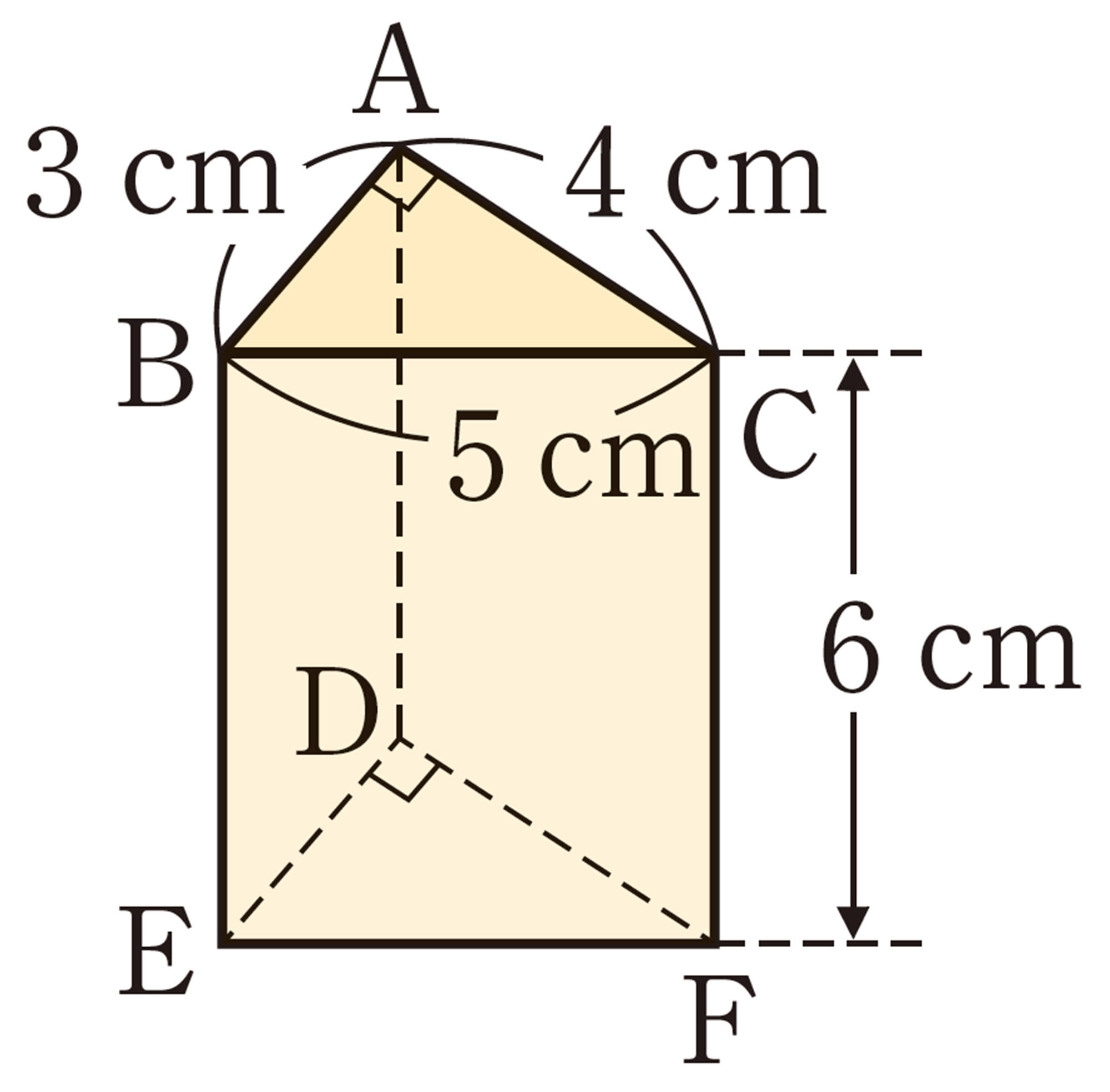
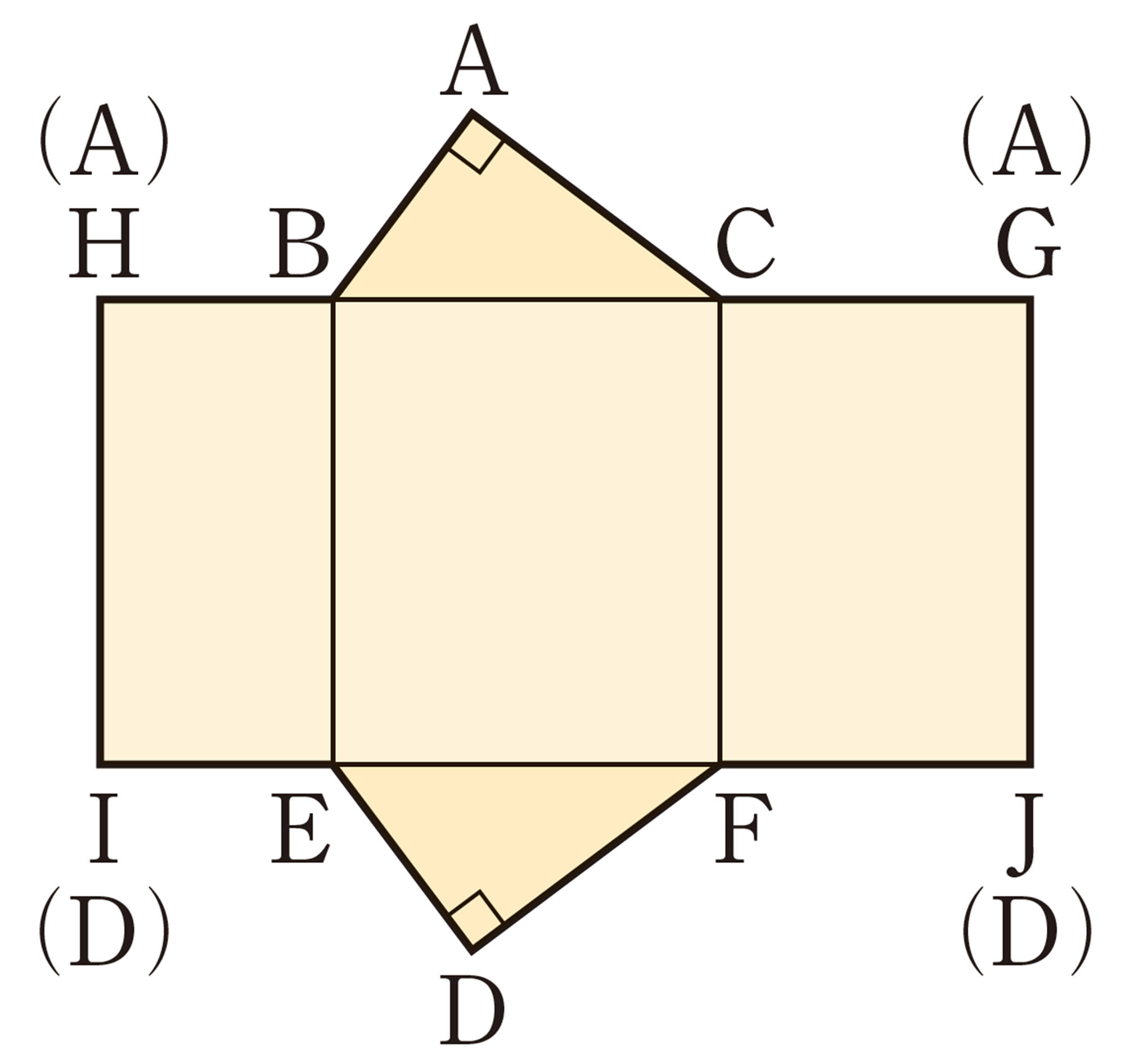
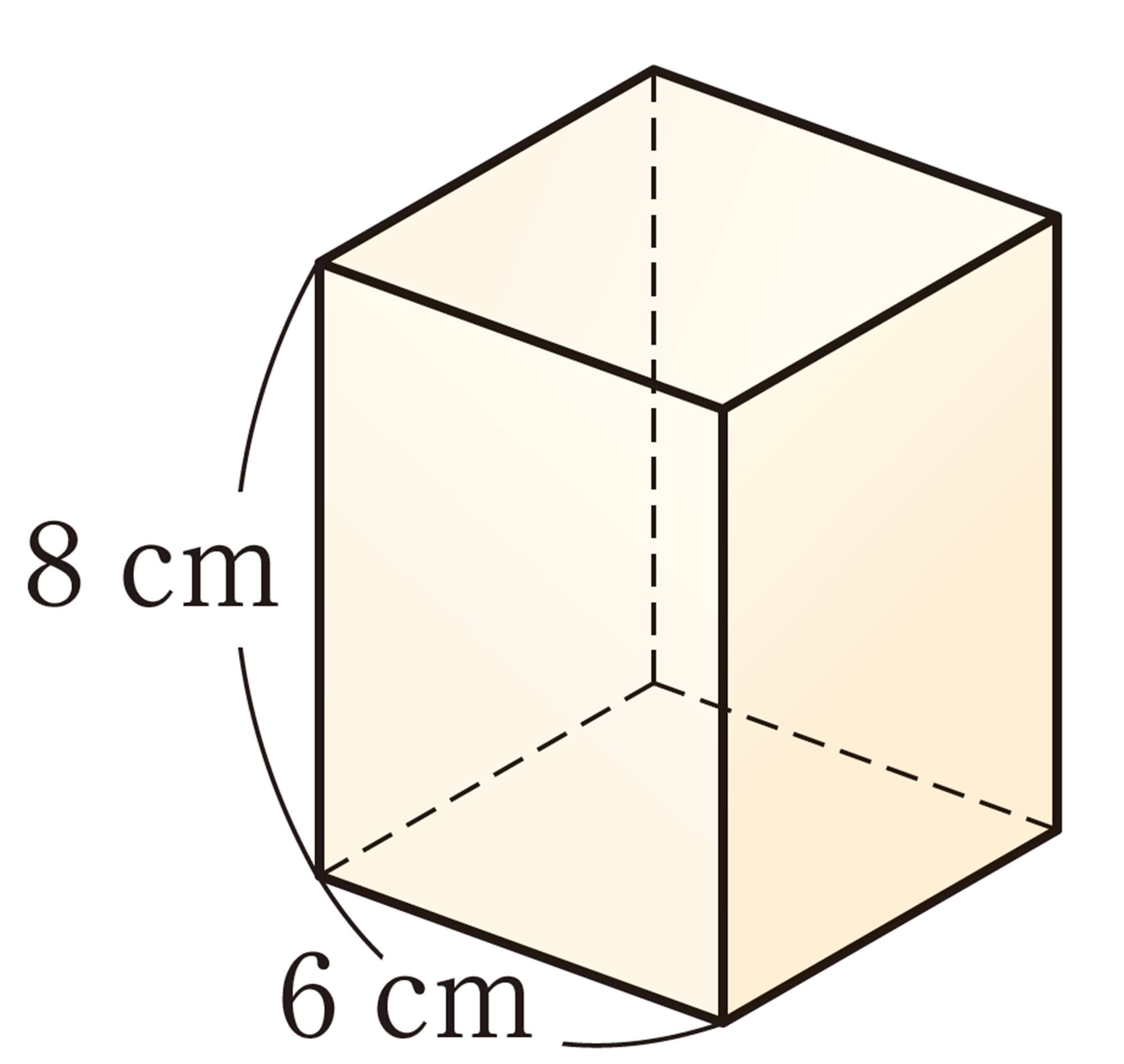
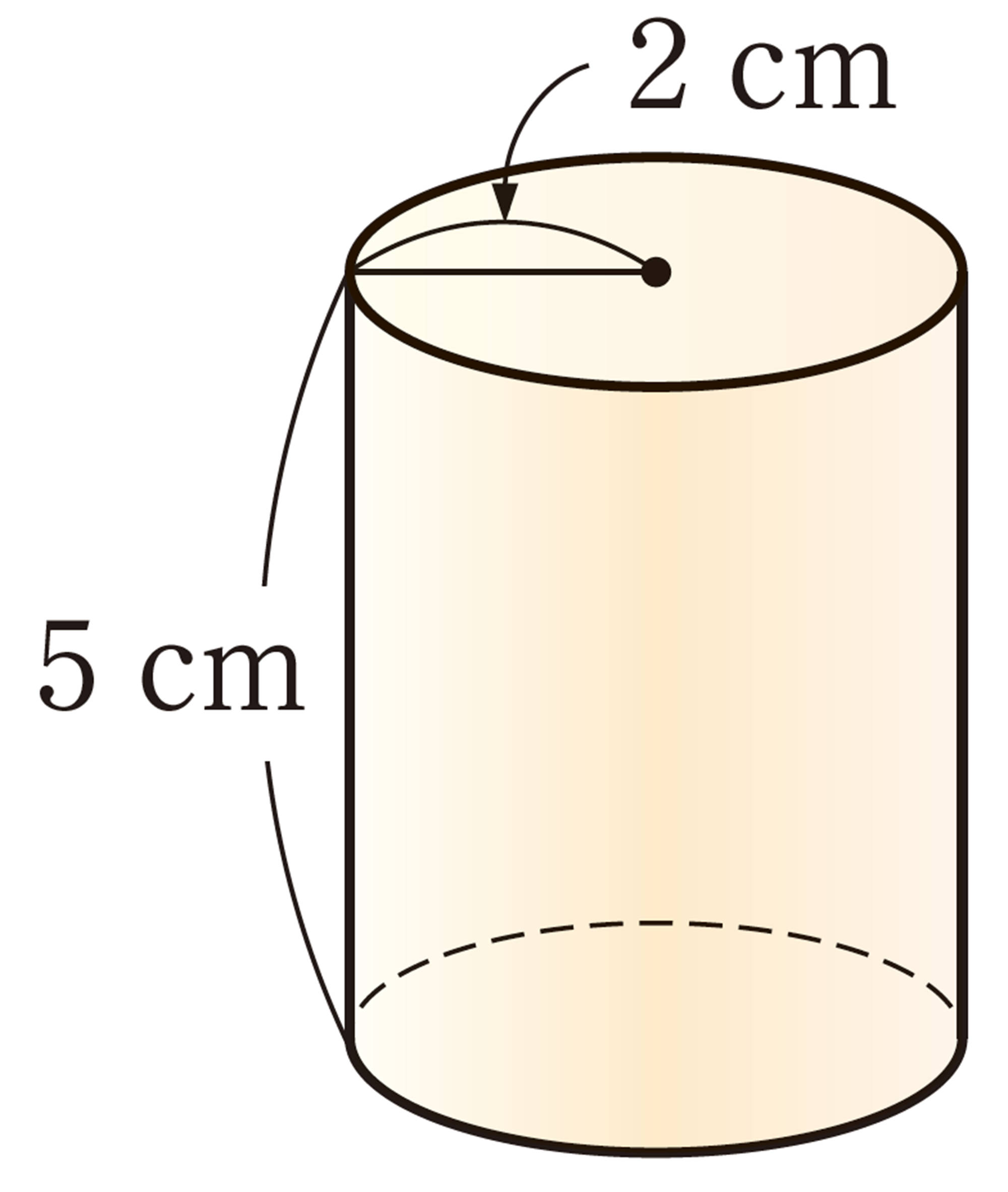
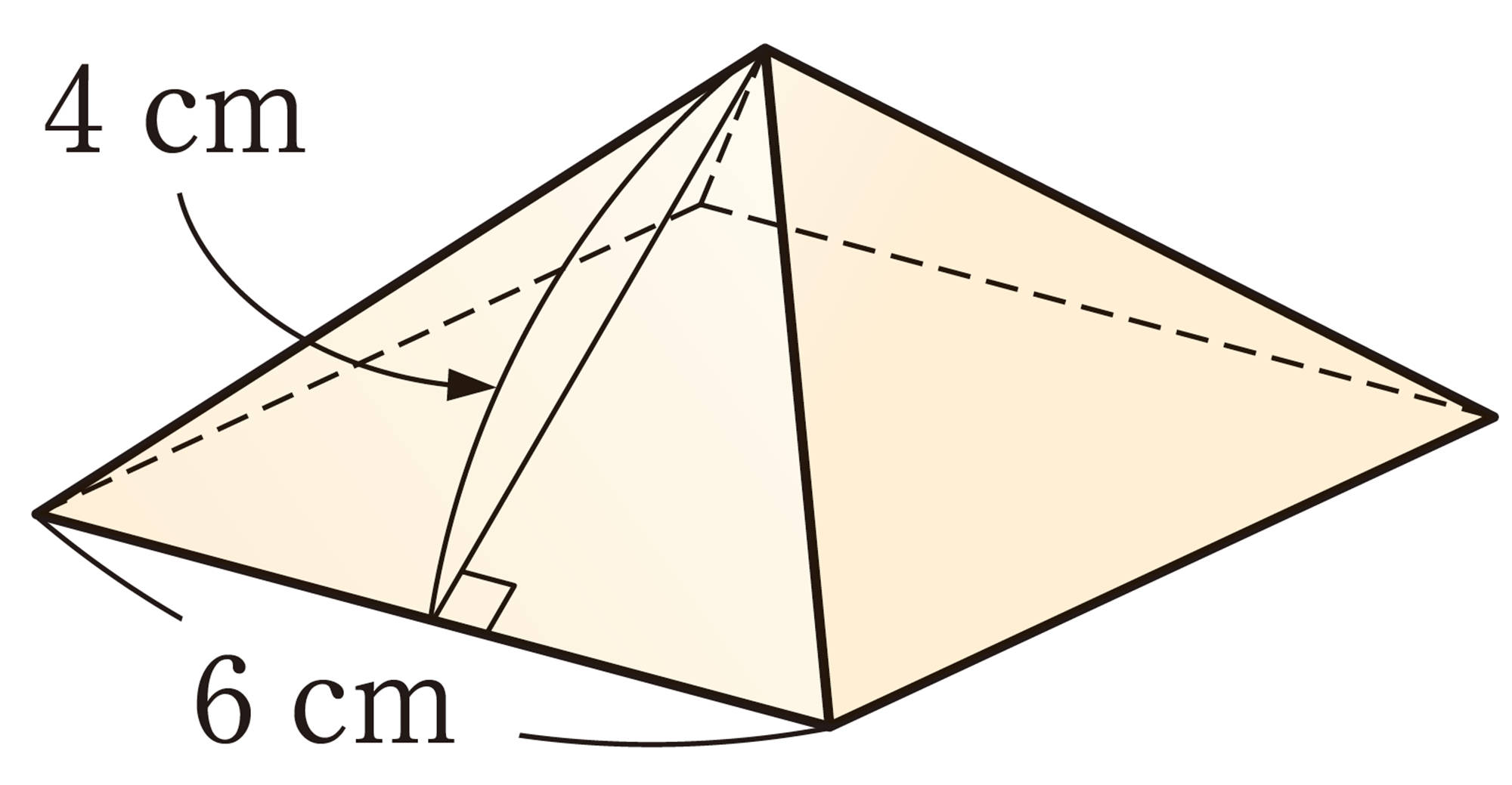
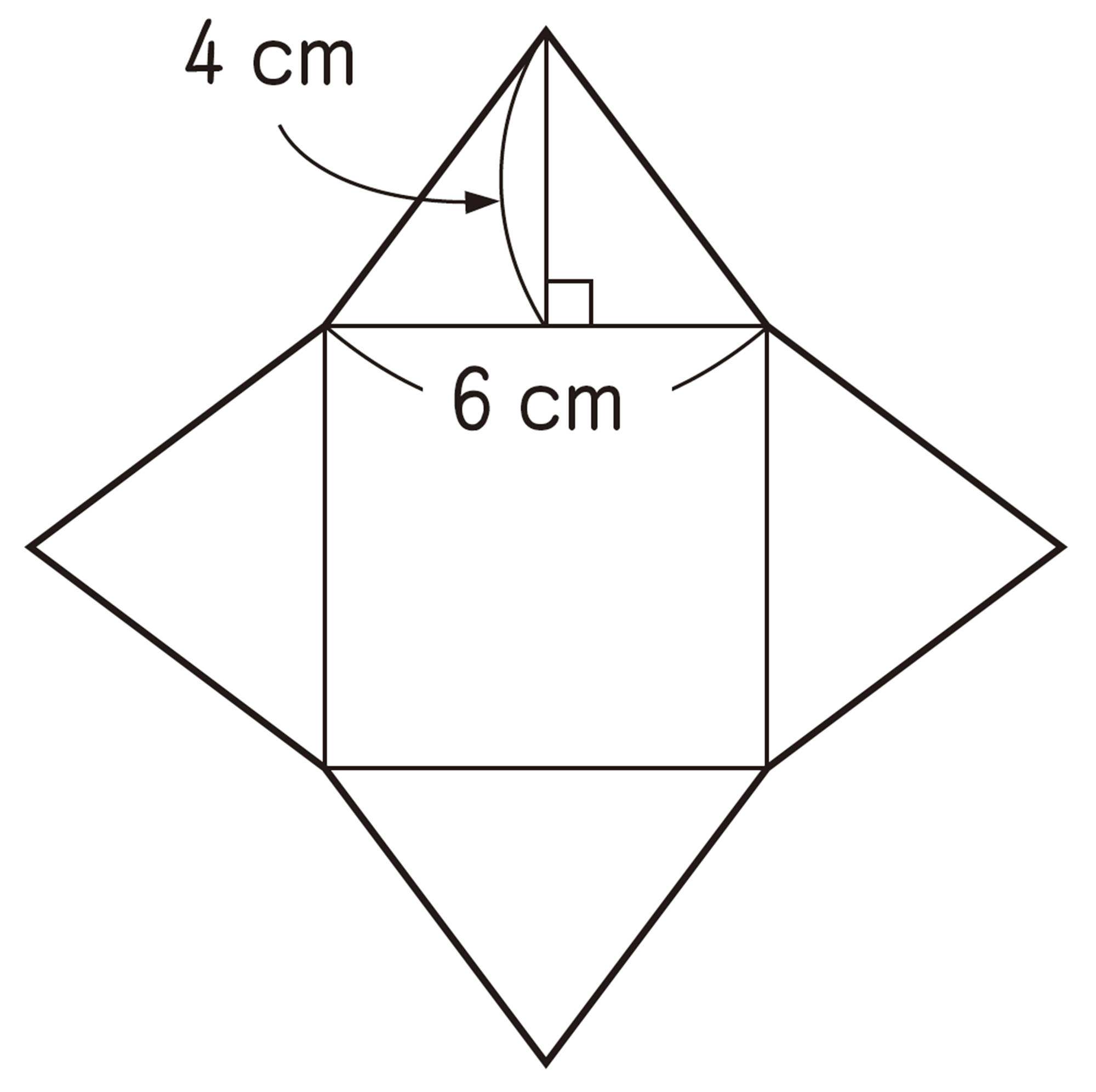
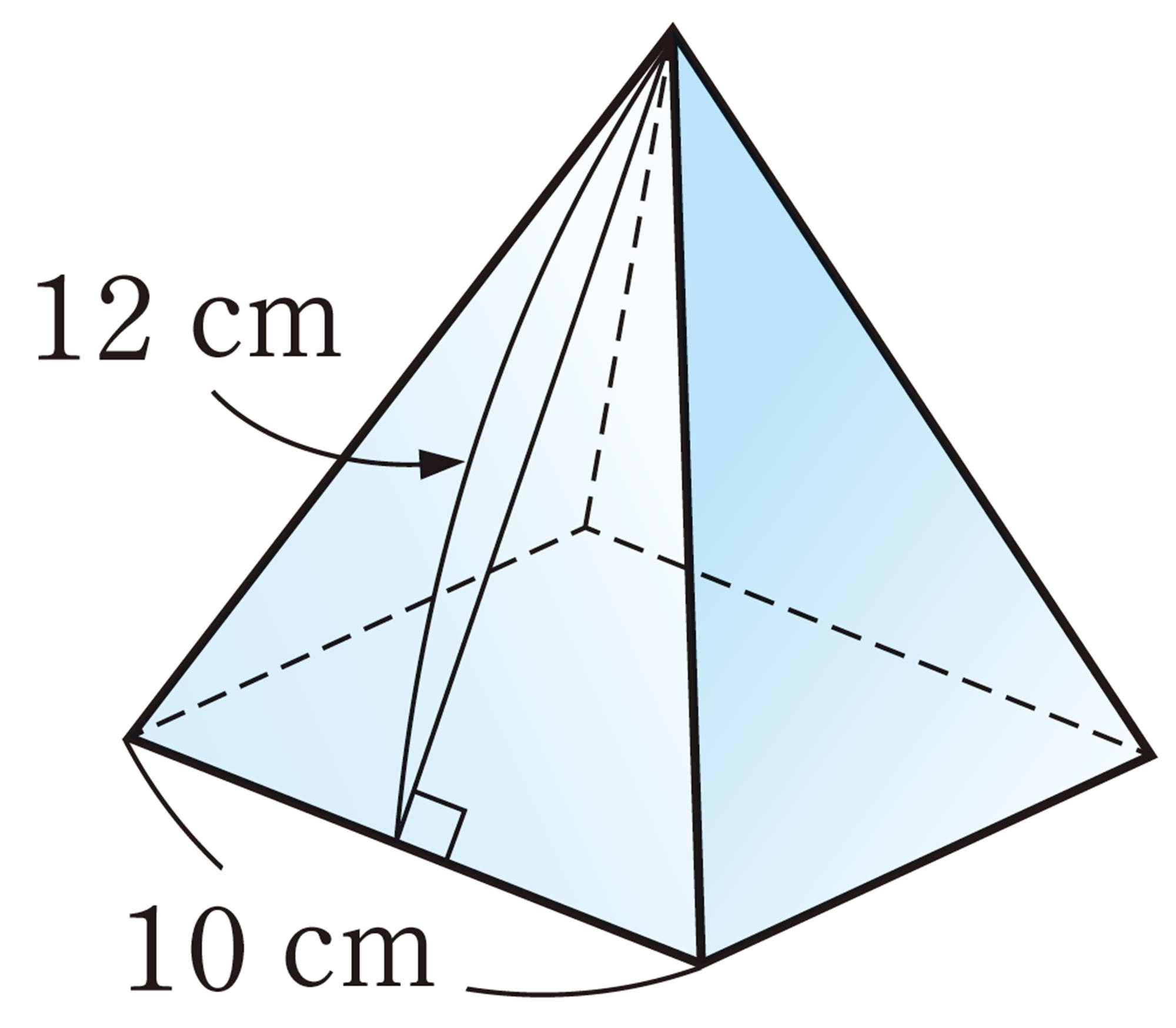
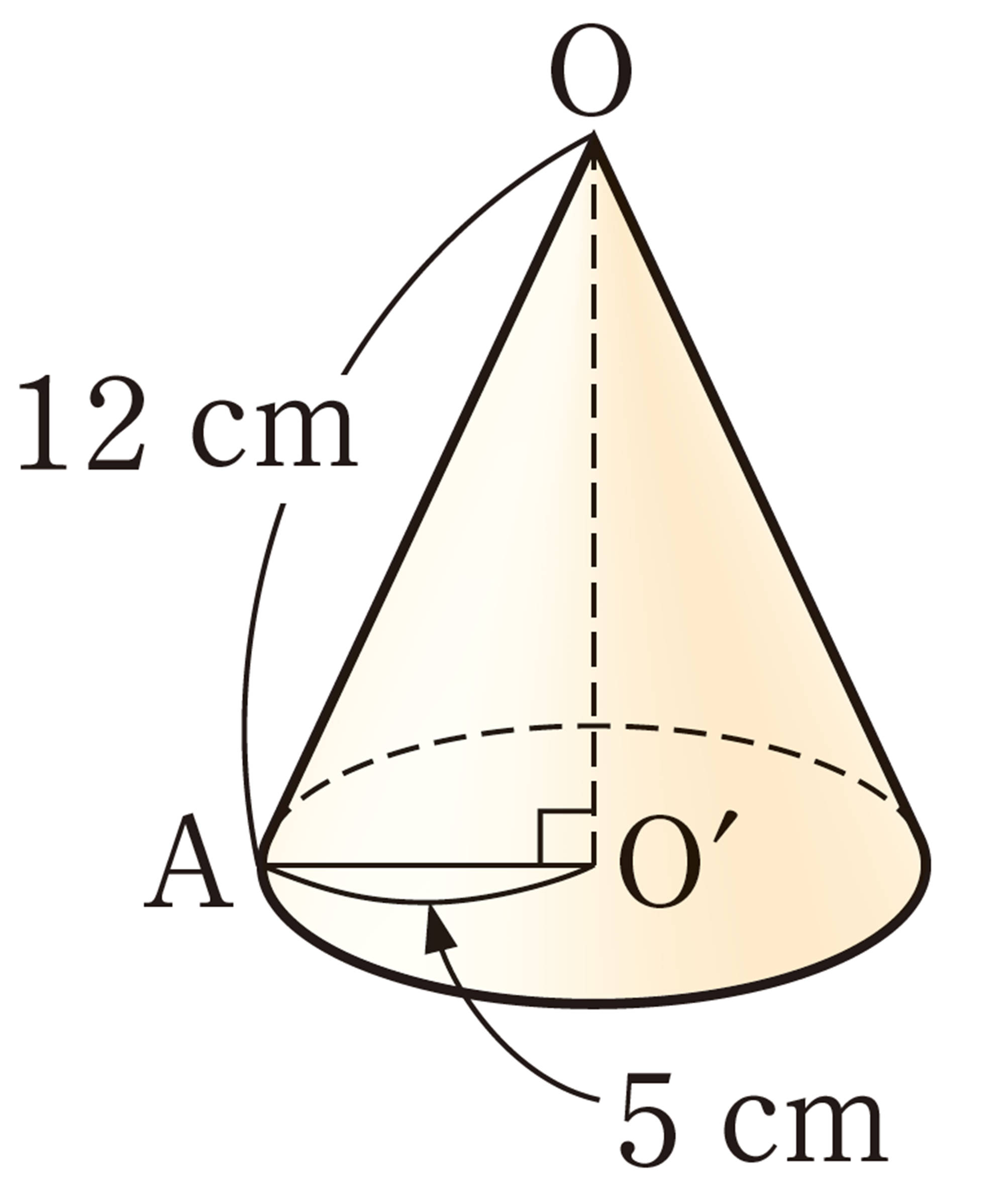
⑴ ㋑の表面全体の面積は，㋒の側面の面積と等しくなります。㋑の表面全体の面積を求めてみましょう。ただし，円周率は[mathjax]\(3.14\)とします。
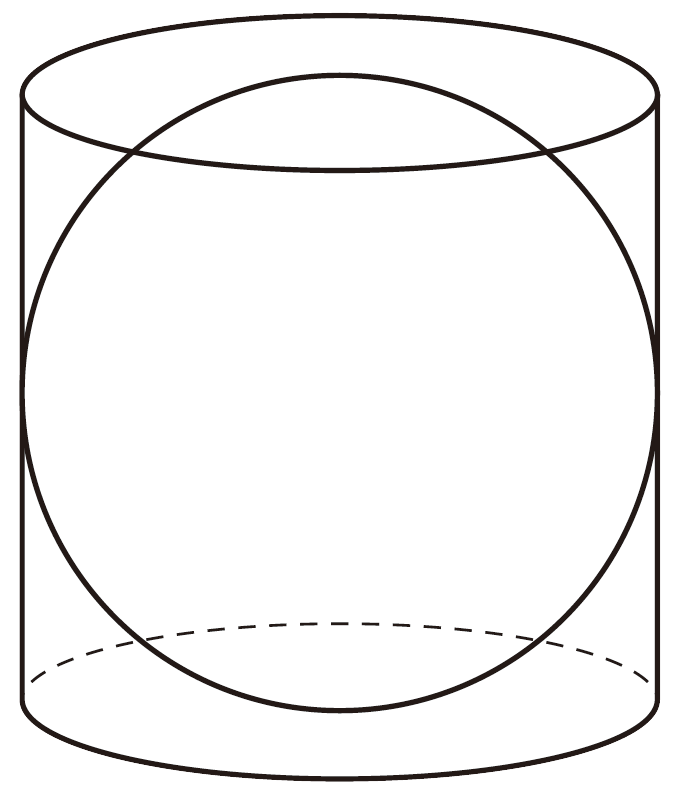
⑵ ㋐，㋑の立体は，上の図のように，㋒の立体の中にぴったり入ります。㋑，㋒の立体の体積は，それぞれ㋐の立体の体積の何倍になるか予想してみましょう。
次の課題へ！
立体の側面の面積や表面の面積を求めることはできるのかな？
P.224
次の課題へ！
円錐や球の体積を求めることはできるのかな？
P.231，234
<1年p.224>
1 立体の表面積
角柱，円柱の表面積
Q Question
右のような円柱の表面全体の面積を求めるには，どこの長さがわかればよいでしょうか。
見方・考え方
立体をどんな表し方にするとわかるかな。
立体を展開図で表せば，求められそうだね。
必要な長さはどこかな。
立体の表面全体の面積を，その立体の 表面積 という。また，1つの底面の面積を 底面積 ，側面全体の面積を 側面積 という。
目標 ▷ 立体の表面積の求め方について考えよう。
問 １ 【Q】の円柱は，底面が半径3 cmの円，高さが7 cmです。展開図は，右の図のようになります。この円柱の底面積，側面積，表面積を求めなさい。ただし，円周率は[mathjax]\(3.14\)とします。
円周率は，円周の直径に対する割合である。その値は， [mathjax]\(3.141592653589793238462643383279\cdots\)
と限りなく続く数となり，この値をギリシャ文字 [mathjax] \( \pi\)で表す。
[mathjax] \( \pi\)は，文字式や方程式で学んだ文字とちがい，特定の数を表しているため，積の中では数のあと，その他の文字の前に書く。
注意 今後，特にことわらない限り，円周率には[mathjax] \( \pi\)を用いるものとする。
<1年p.225>
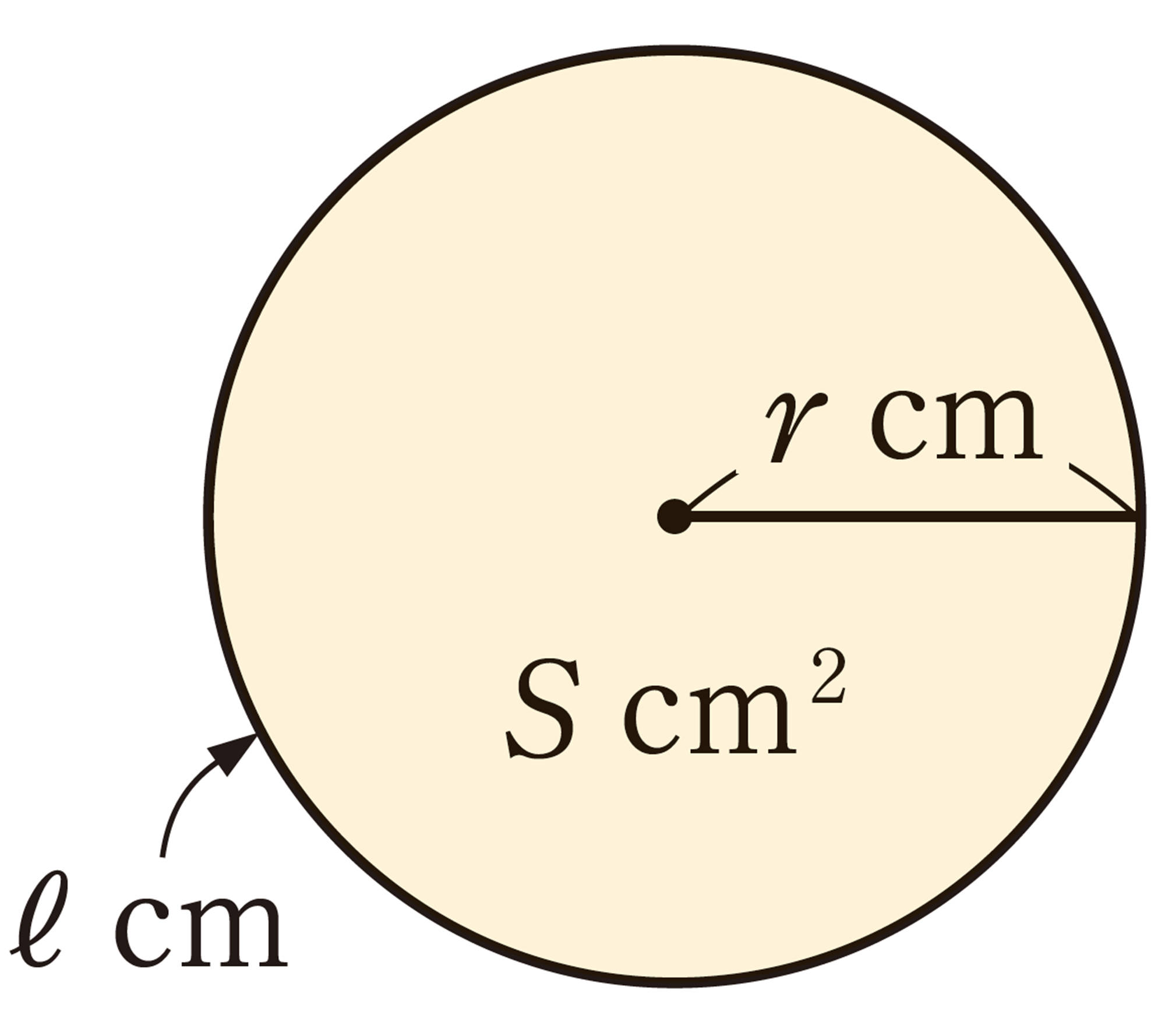
例 １ 半径r cmの円について，円周の長さは[mathjax] \( 2 \pi r\)cm面積は[mathjax] \( \pi r^{2}\)cm²である。
一般に，半径r cmの円の円周の長さをℓ cm，面積を[mathjax] \( S \) cm²
とすると，
[mathjax]\(ℓ=2\pi r\)，[mathjax] \( S=\pi r^{2}\)
と表すことができる。
注意 [mathjax] \( r \)はradius(半径)，[mathjax] \( ℓ \)はlength(長さ)，[mathjax] \( S \)はsurface area(表面積)の頭文字である。
問 ２ 半径7 cm の円の円周の長さと面積を求めなさい。
問 ３ 次のような三角柱の底面積，側面積，表面積を求めなさい。
角柱や円柱の表面積について，次のことがいえる。
[mathjax]\(\text{( 表面積 )} = \text{( 側面積 )}+\text{( 底面積 )}\times 2\)
問 ４ 次の立体の表面積を求めなさい。
⑴ 正四角柱
⑵ 円柱
<1年p.226>
角錐，円錐の表面積
例 ２ 右の正四角錐の表面積を求めなさい。
考え方 底面積，側面積をそれぞれ求め，それらを加えればよい。
解答
底面は1 辺6 cm の正方形であるから，
底面積は，
[mathjax]\(6\times 6=36\)
より， [mathjax] \(36\)cm²
また， 側面は底辺6 cm， 高さ4 cm の
二等辺三角形で， それが4 つあるから，
側面積は，
[mathjax]\(\left(\dfrac{1}{2}\times 6\times 4\right) \times 4=48 \)
より， [mathjax] \(48\)cm²
したがって， 表面積は，
[mathjax] \(36+48=84 \)
答 [mathjax] \(84\)cm²
説明をわかりやすくするために，図をきちんとかいておこう。
問５ 右の正四角錐の底面積，側面積，表面積を求めなさい。
Q Question
右のような円錐の表面積を求めるには，どこの長さがわかればよいでしょうか。
円柱のときのように，展開図にすれば求められるかな。
側面はおうぎ形になるけど，面積は求められるかな。
見方・考え方
円柱の表面積を求めたときと同じように考えられるかな。
<1年p.227>
円錐の表面積を求めるために，おうぎ形の面積について調べてみよう。
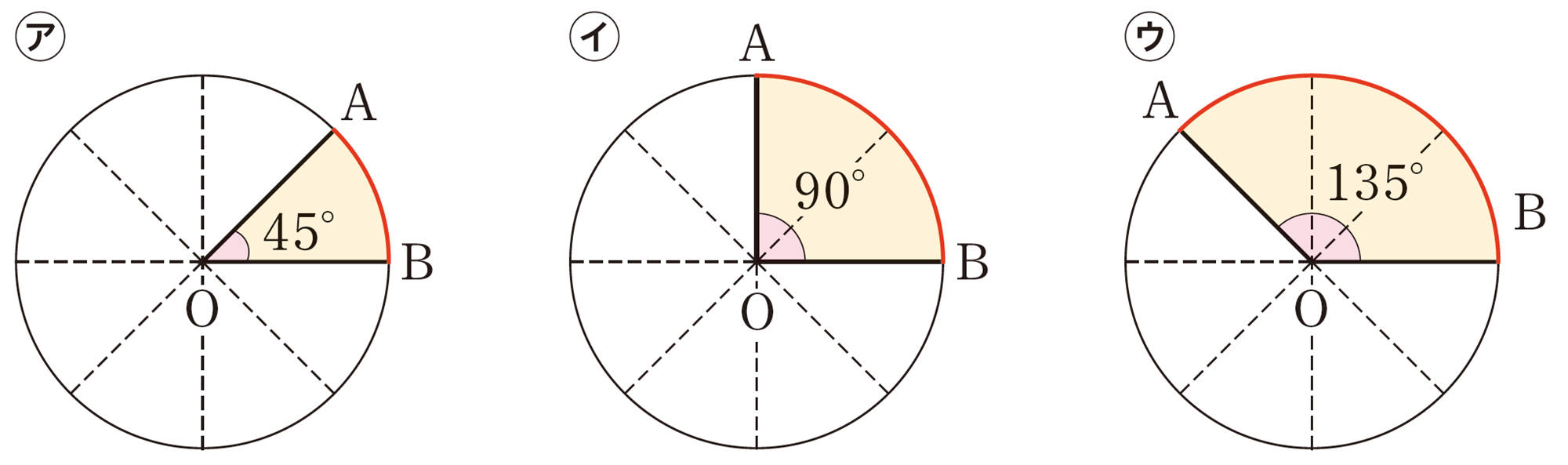
例 ３ 次の図のように，おうぎ形の半径を変えずに，中心角を2倍，3倍，…にしていくと，弧の長さも，面積も2倍，3倍，…になる。
例3から，次のことがわかる。
1つの円では，おうぎ形の弧の長さは中心角の大きさに比例する。
おうぎ形の面積は中心角の大きさに比例する。
問 ６ 1 つの円で，おうぎ形の面積は弧の長さに比例するといえますか。
問 ７ 半径6 cm，中心角[mathjax]\(120^{\circ}\)のおうぎ形について，次の問いに答えなさい。
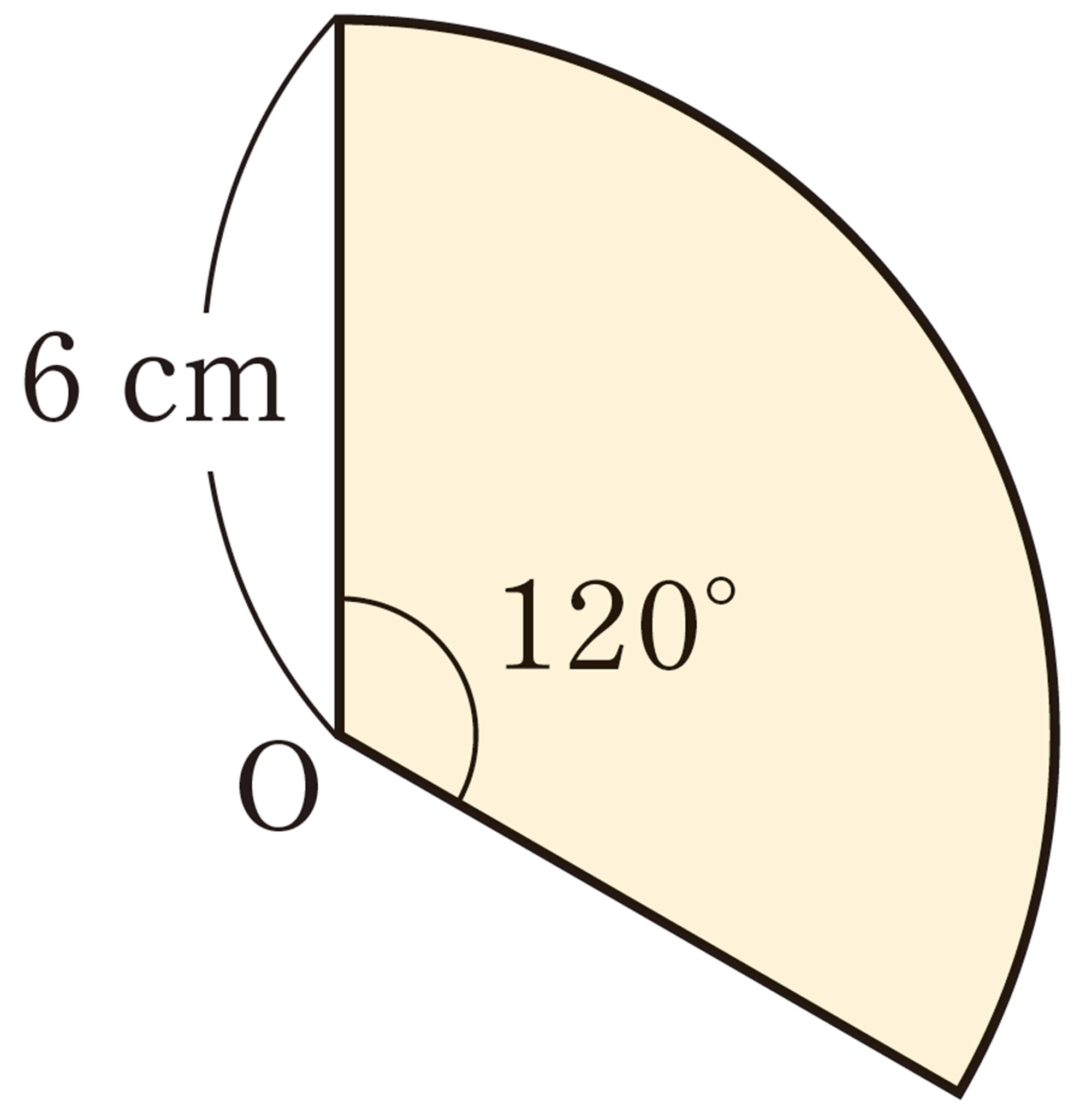
⑴ このおうぎ形の面積は，同じ半径の円の面積の何倍ですか。
⑵ 面積を求めなさい。
⑶ 弧の長さを求めなさい。
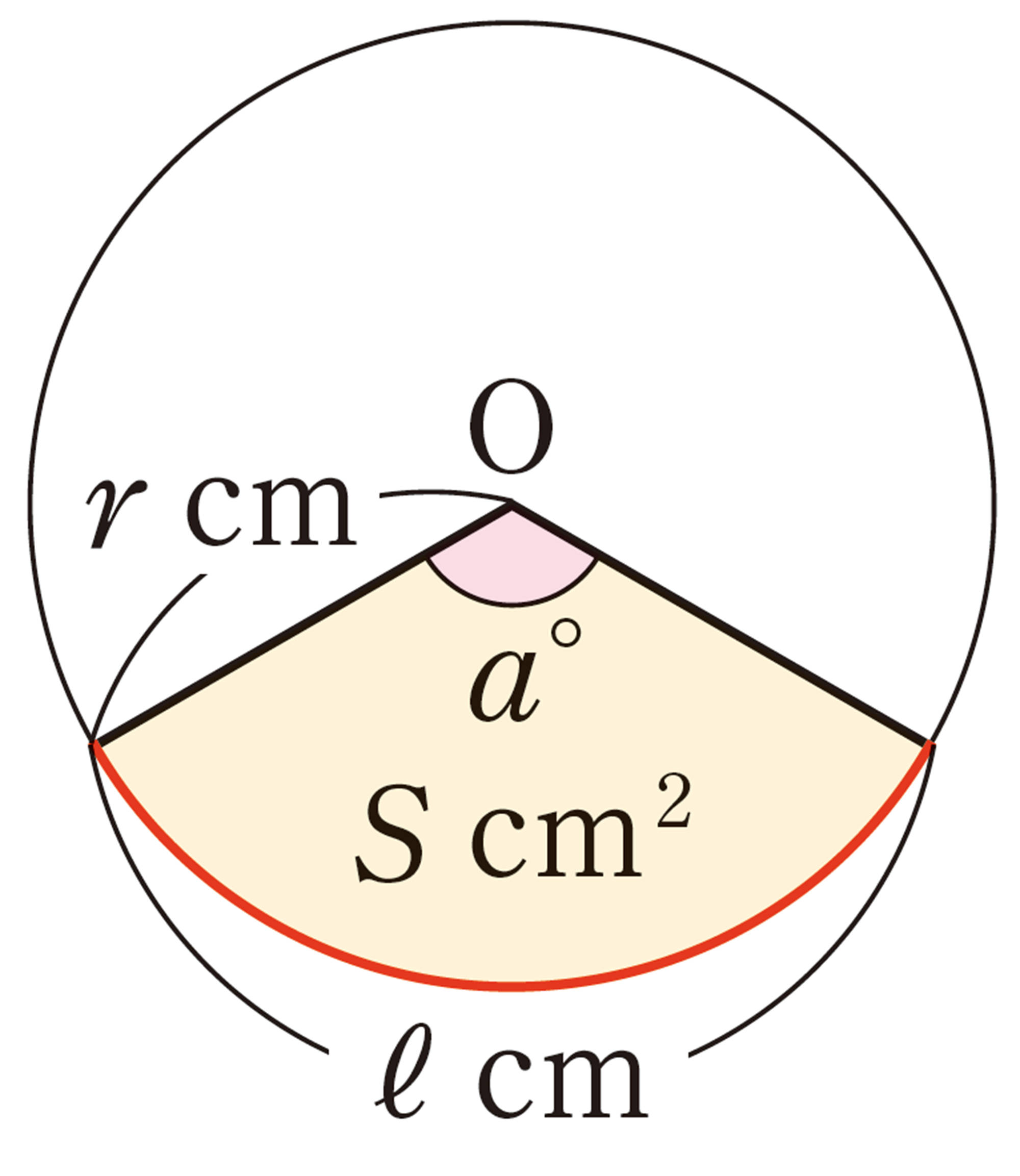
おうぎ形の弧の長さと面積は，次の式で求めることができる。
おうぎ形の弧の長さと面積
半径r cm，中心角[mathjax]\(a^{\circ}\)のおうぎ形の弧の長さを ℓ cm，面積をS cm²とすると，
[mathjax] \(ℓ=2\pi r\times \dfrac{a}{360}\)，[mathjax] \(S=\pi r^{2}\times \dfrac{a}{360}\)
問 ８ 半径4cm，中心角[mathjax]\(135^{\circ}\)のおうぎ形の弧の長さと面積を求めなさい。
<1年p.228>
Q Question
右の図のような，底面の半径が5 cm，母線の長さが12 cmの円錐があります。この円錐の側面積は何cm²でしょうか。どのように求めればよいか話し合ってみましょう。
おうぎ形の面積は，半径と中心角がわかれば求められるね。
弧の長さと中心角が比例することが使えるかな。
見方・考え方
おうぎ形のどこに着目して考えればいいかな。
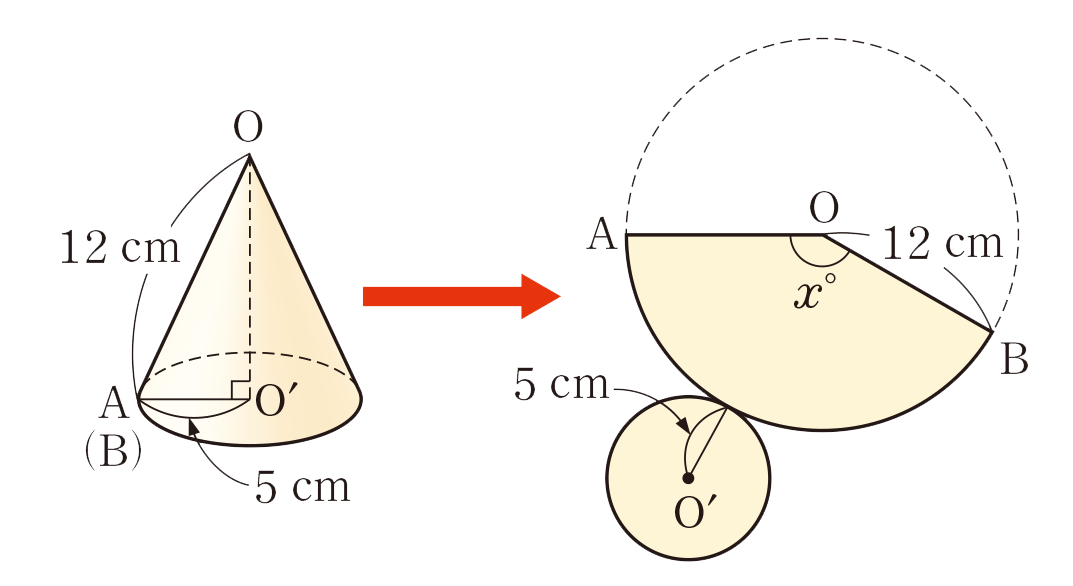
１ 拓真さんは，側面のおうぎ形の面積を求めるには，その中心角を求めればよいと考えました。拓真さんの考えを読み，下の問いに答えましょう。
拓真さんの考え
おうぎ形OABの[mathjax] \( \stackrel{\huge\frown}{AB} \)の長さは，[mathjax] \( 2\pi \times 5\)cm‥‥‥㋐
円Oの円周の長さは，[mathjax]\(\boxed{\phantom{0000}}\) cm
したがって，おうぎ形OABの中心角を[mathjax] \( x^{\circ}\)とすると，
⑴ ㋐の理由を説明しましょう。
⑵ [mathjax]\(\boxed{\phantom{000}}\)にあてはまる式を書きましょう。
⑶ 中心角[mathjax] \( x \)の値が㋑の式で求められる理由を説明しましょう。
⑷ ㋒の式から，どんなことが読み取れるでしょうか。
<1年p.229>
２ 中心角が[mathjax]\(150^{\circ}\)であることを使って，おうぎ形OABの面積(円錐の側面積)を求めてみましょう。
中心角がわかれば，おうぎ形の面積が求められたね。
でも，おうぎ形の中心角を求める必要があるのかな。
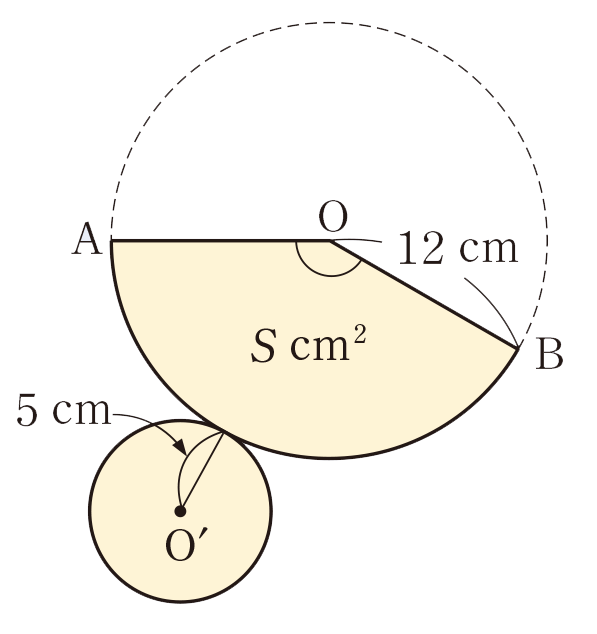
３ 美月さんは，おうぎ形の中心角を求めなくても，面積が求められると考えました。美月さんは，これまで学んできたどんなことを根拠にして側面積を求めたのでしょうか。美月さんの考え方を説明してみましょう。
美月さんの考え
円Oの面積は，[mathjax] \( \left( \pi \times 12²\right) \)cm²
したがって，おうぎ形OABの面積を
[mathjax] \( S \)cm²とすると，
答 [mathjax] \( 60\pi \)cm²
４ 拓真さんの考えや美月さんの考えから，円錐の側面積の求め方について，どんなことがわかるかを話し合ってみましょう。
５ 前ページの【Q】の円錐の底面積と表面積を求めてみましょう。
問 ９ 右の円錐の底面積，側面積，表面積を，前ページの【１】の拓真さんや【３】の美月さんの考えを使って求めなさい。
どんなことがわかったかな
角柱や円柱，角錐，円錐の表面積は，展開図をもとに求めることができます。
次の課題へ！
球の表面積も同じように求めることができるのかな？
↓P.234
<1年p.230>
弧の長さとおうぎ形の面積 Tea Break
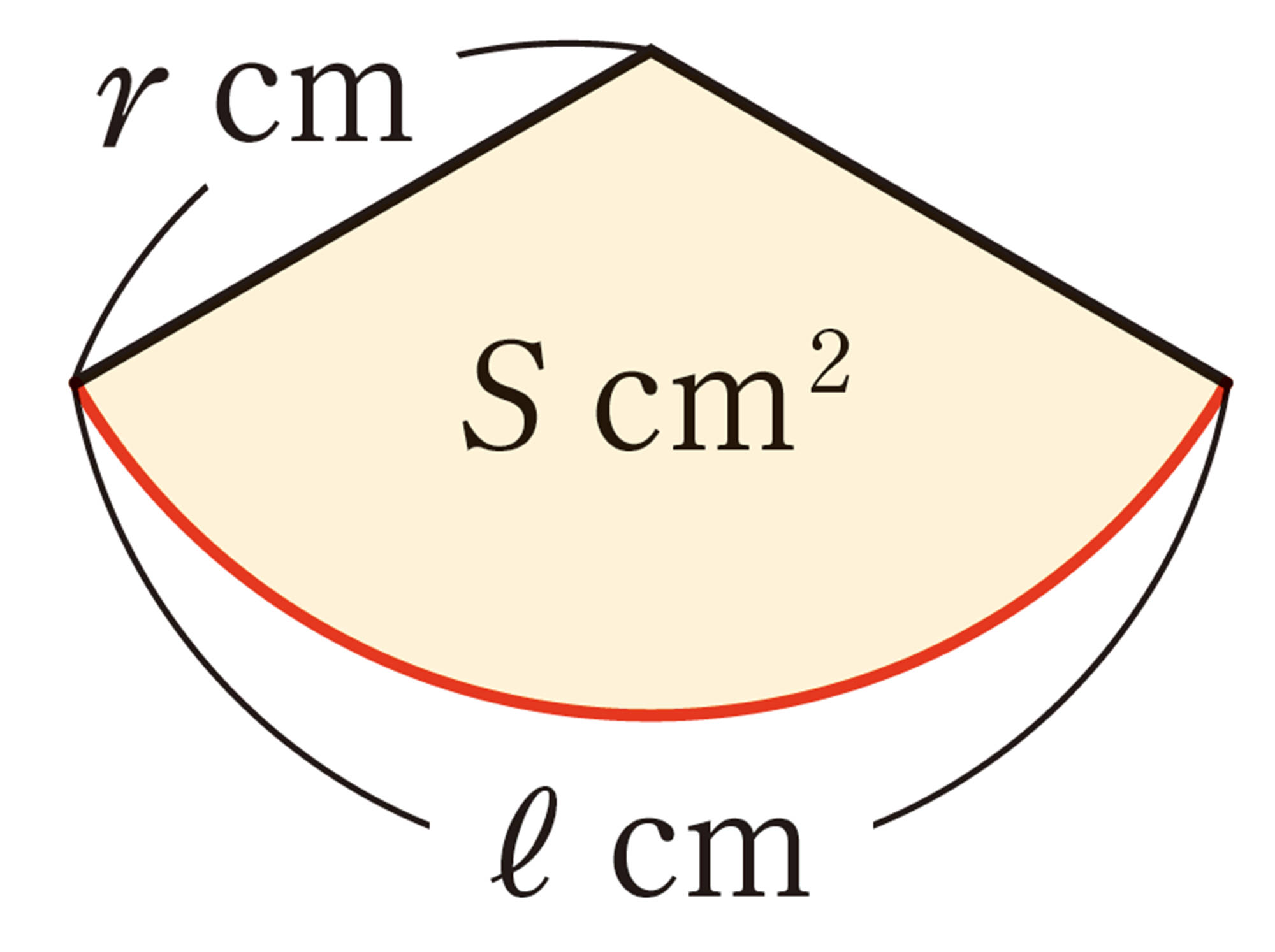
半径rcm，弧の長さ ℓ cmのおうぎ形の面積[mathjax] \( S \) cm² について考えてみましょう。
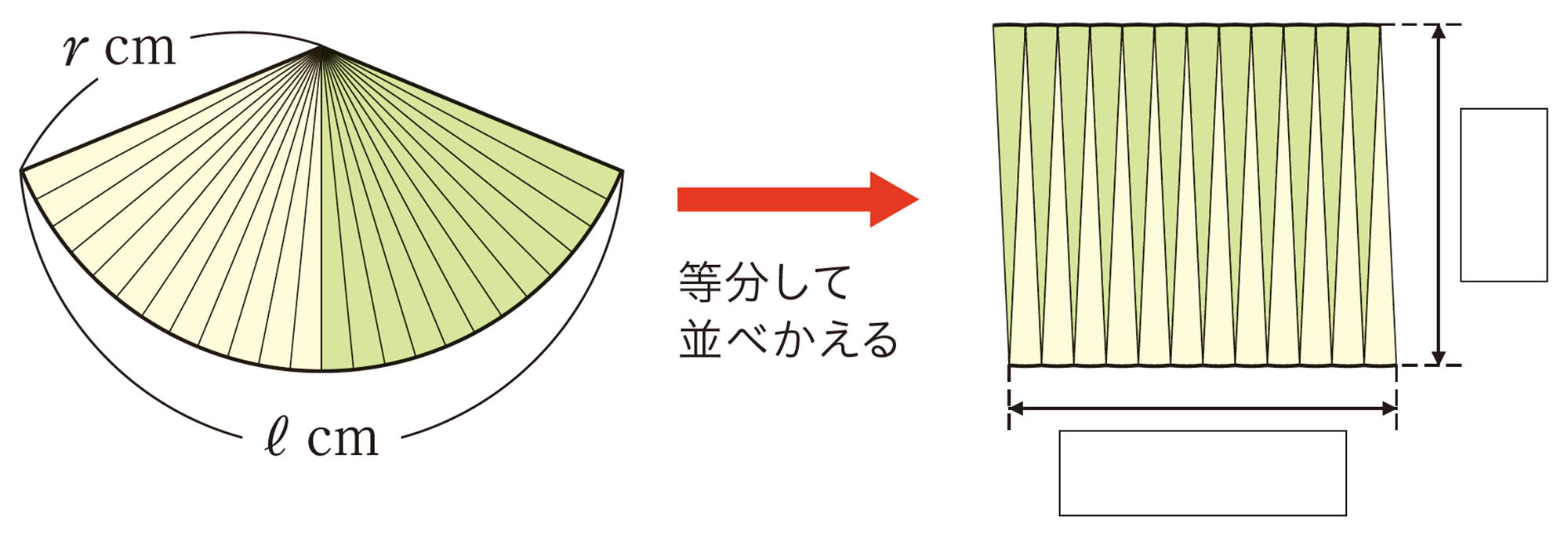
【１】 次の図のように，おうぎ形を等分して並べかえた図形を長方形とみなすと，長方形の縦と横の長さは，もとのおうぎ形のどの部分の長さと等しくなるでしょうか。
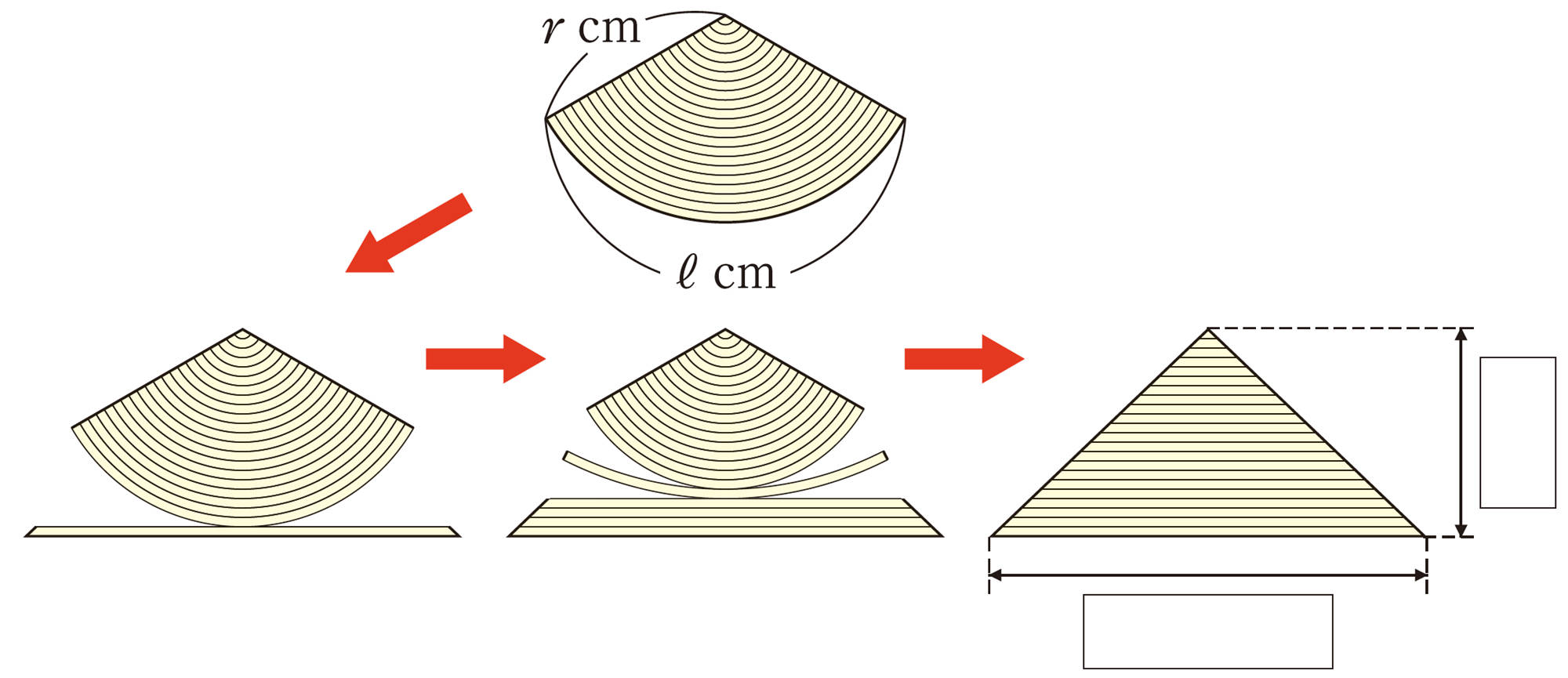
【２】 次の図のように，おうぎ形を分割して並べかえた図形を三角形とみなすと，三角形の底辺と高さは，もとのどの部分の長さと等しくなるでしょうか。
【１】からも，【２】からも，次の式を導くことができます。
おうぎ形の半径をr cm，弧の長さを ℓ cm，面積を[mathjax] \( S \) cm²とすると，
[mathjax] \( S= \dfrac{1}{2}ℓr \)
三角形の面積の公式と似ているね。
【３】 半径4 cm，弧の長さ[mathjax] \( 6\pi \) cmのおうぎ形の面積を求めてみましょう。
