<1年p.198>
5章のまとめの問題 解答P.305〜306 基本
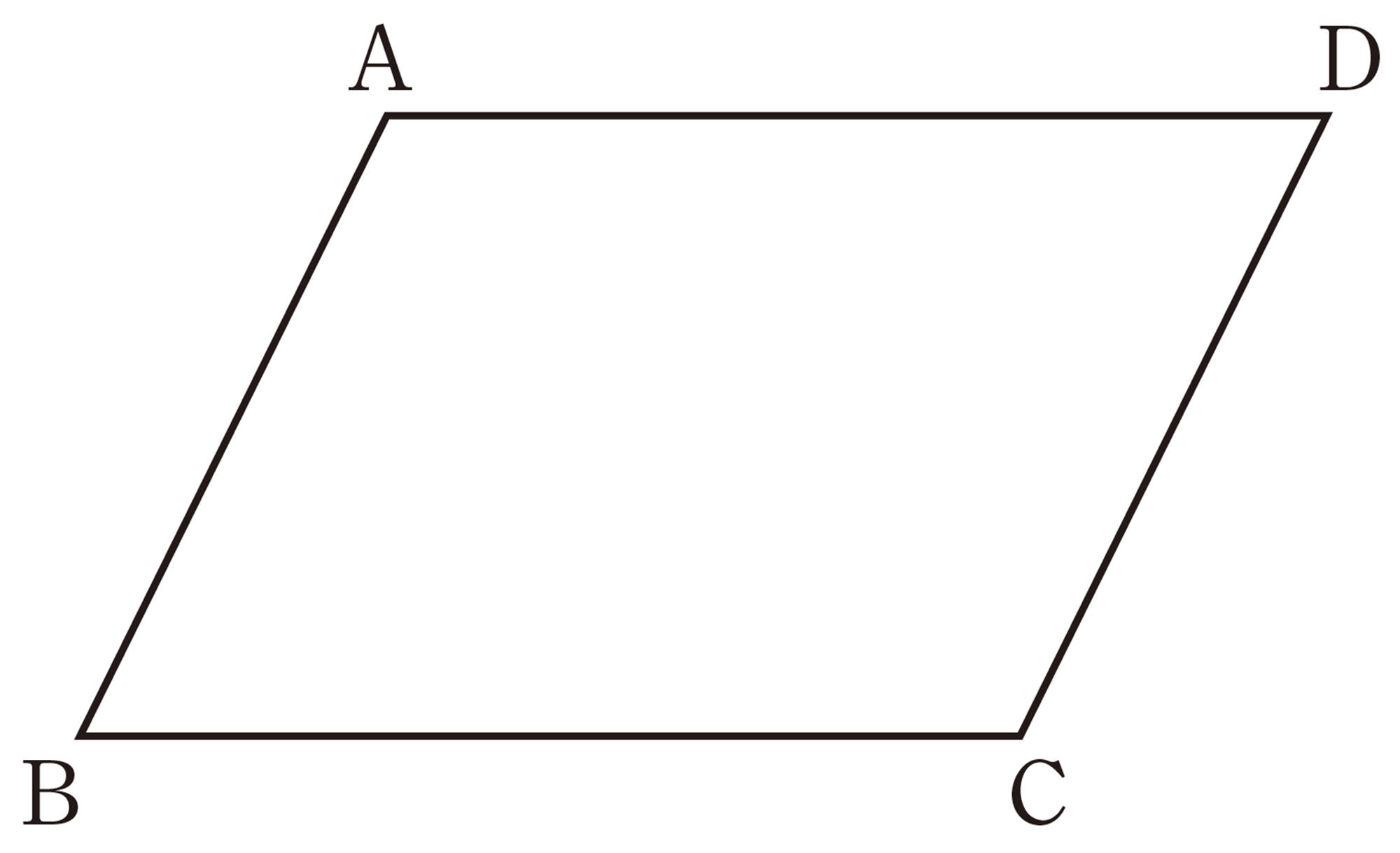
１ 下の図の平行四辺形ABCDについて，次の問いに答えなさい。
⑴ 平行な辺の組を，記号を使って表しなさい。
⑵ 辺CDの垂直二等分線を作図しなさい。
⑶ 辺BCを底辺とするとき，高さを示す線分を作図しなさい。
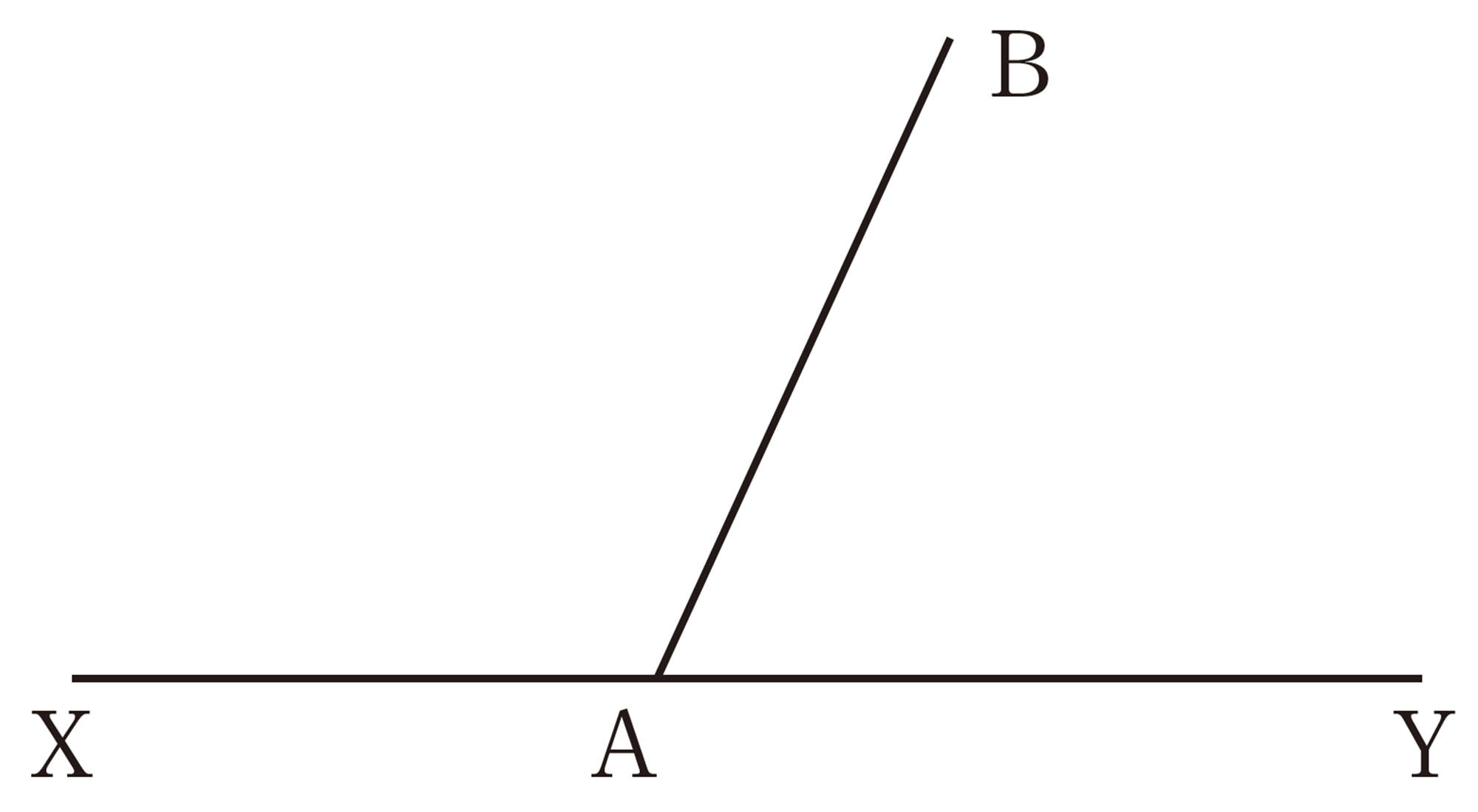
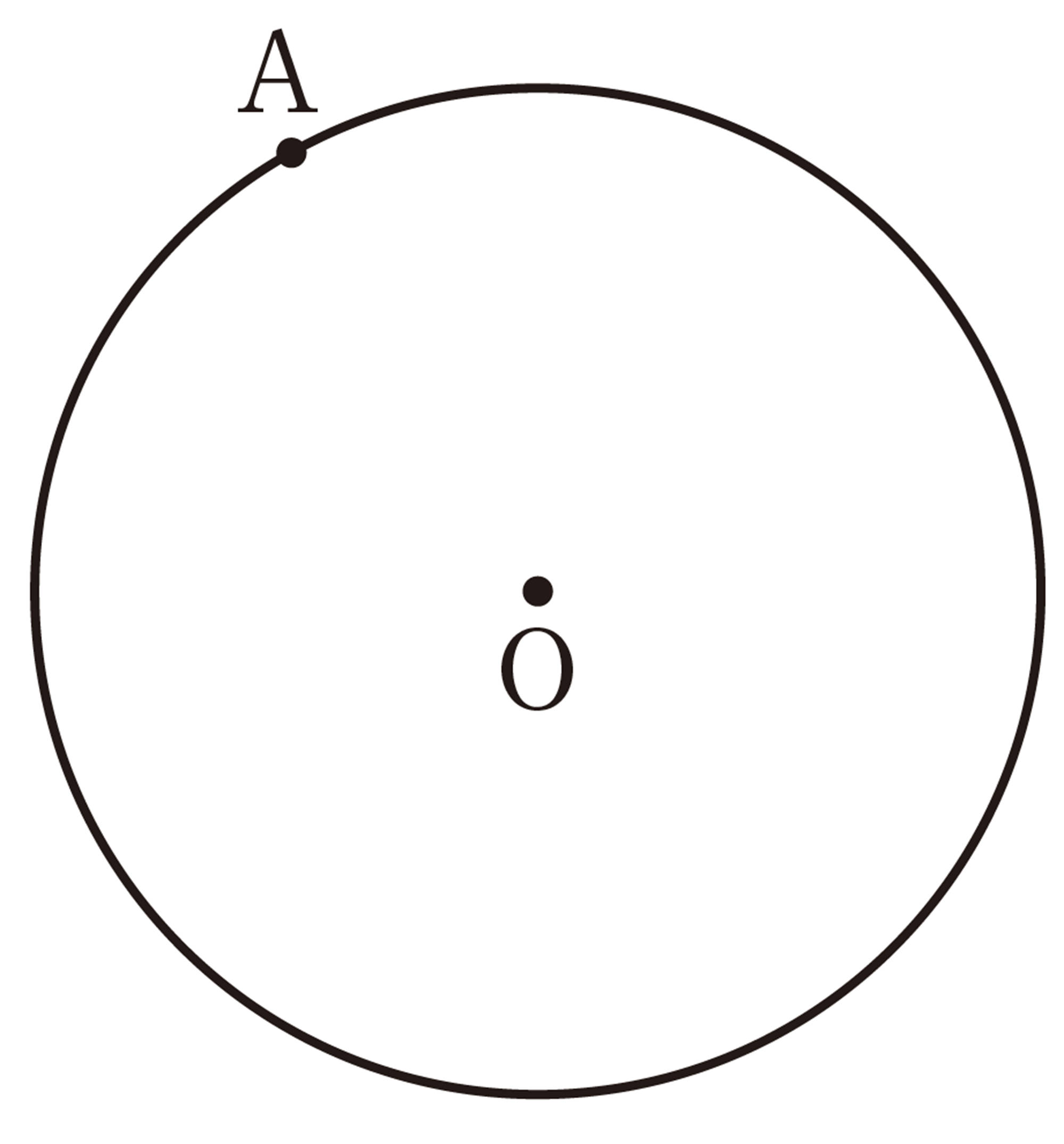
２ 下の図は，直線XY上の点Aから半直線ABを引いたものです。次の問いに答えなさい。
⑴ [mathjax]\(\angle BAX\)の二等分線APと[mathjax]\(\angle BAY\)の二等分線AQを作図しなさい。
⑵ [mathjax]\(\angle PAQ\)の大きさを求めなさい。
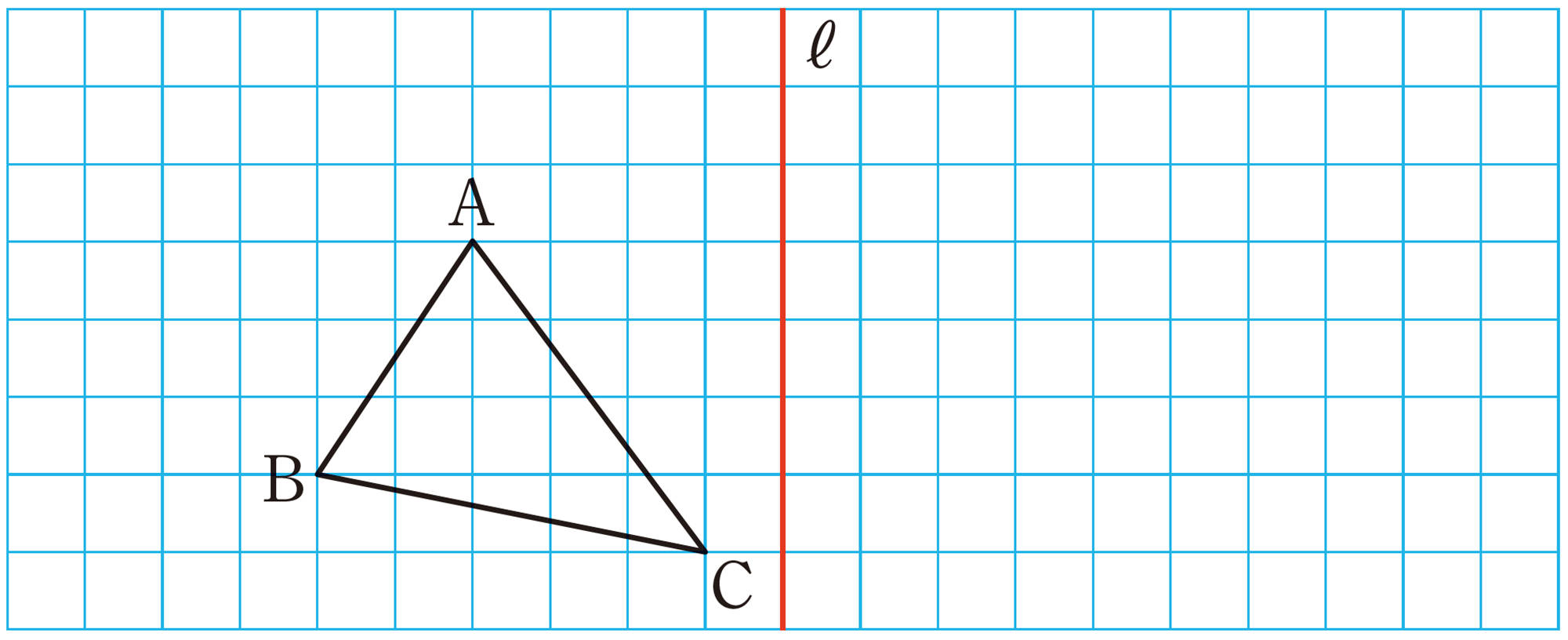
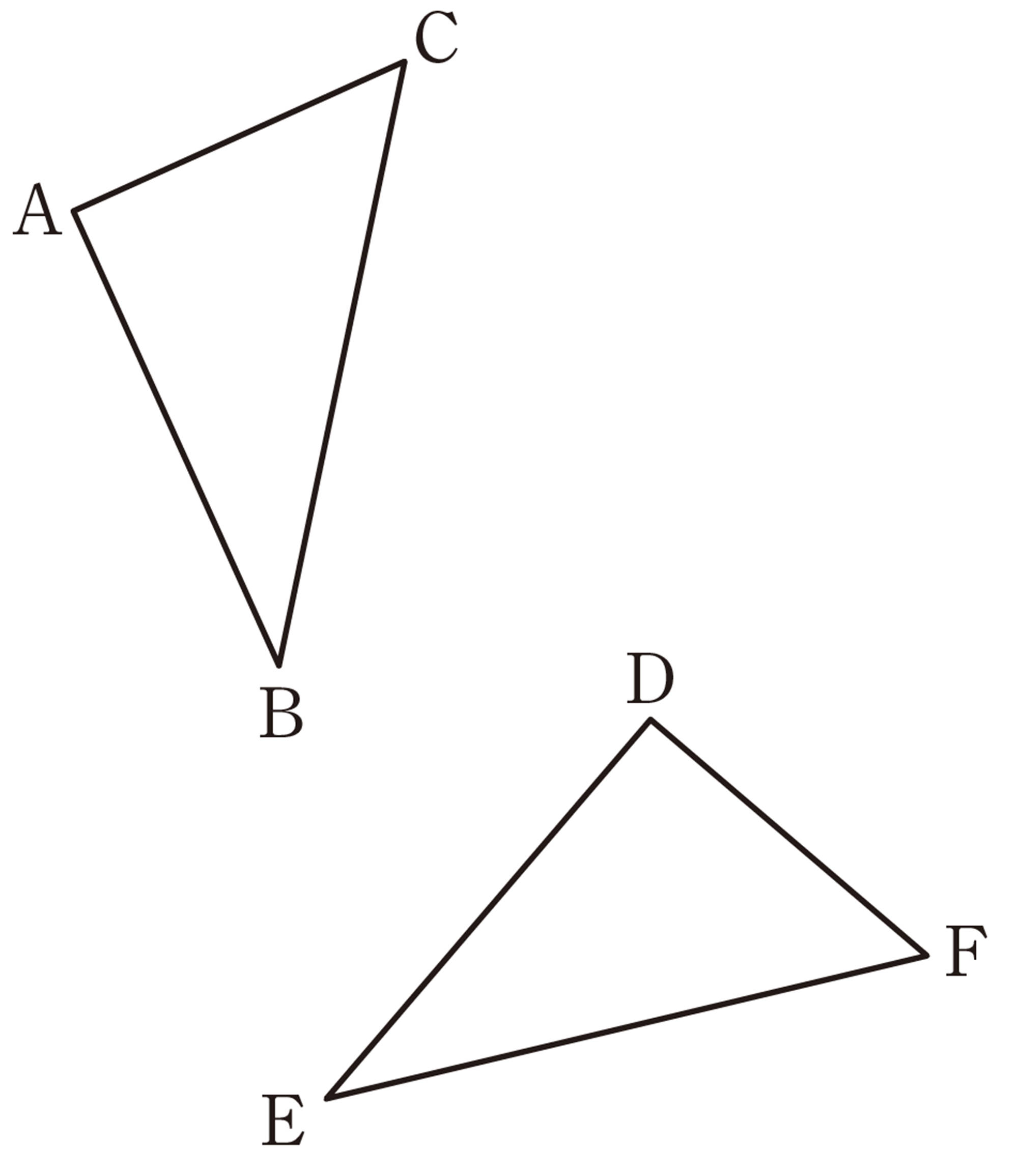
３ 次の図で，[mathjax]\(\triangle ABC\)を，点Bを回転の中心として反時計回りの方向に[mathjax]\(90^{\circ}\)回転移動した[mathjax]\(\triangle DBE\) をかきなさい。また，[mathjax]\(\triangle ABC\)を，直線ℓを対称の軸として対称移動した[mathjax]\(\triangle FGH\)をかきなさい。
<1年p.199>
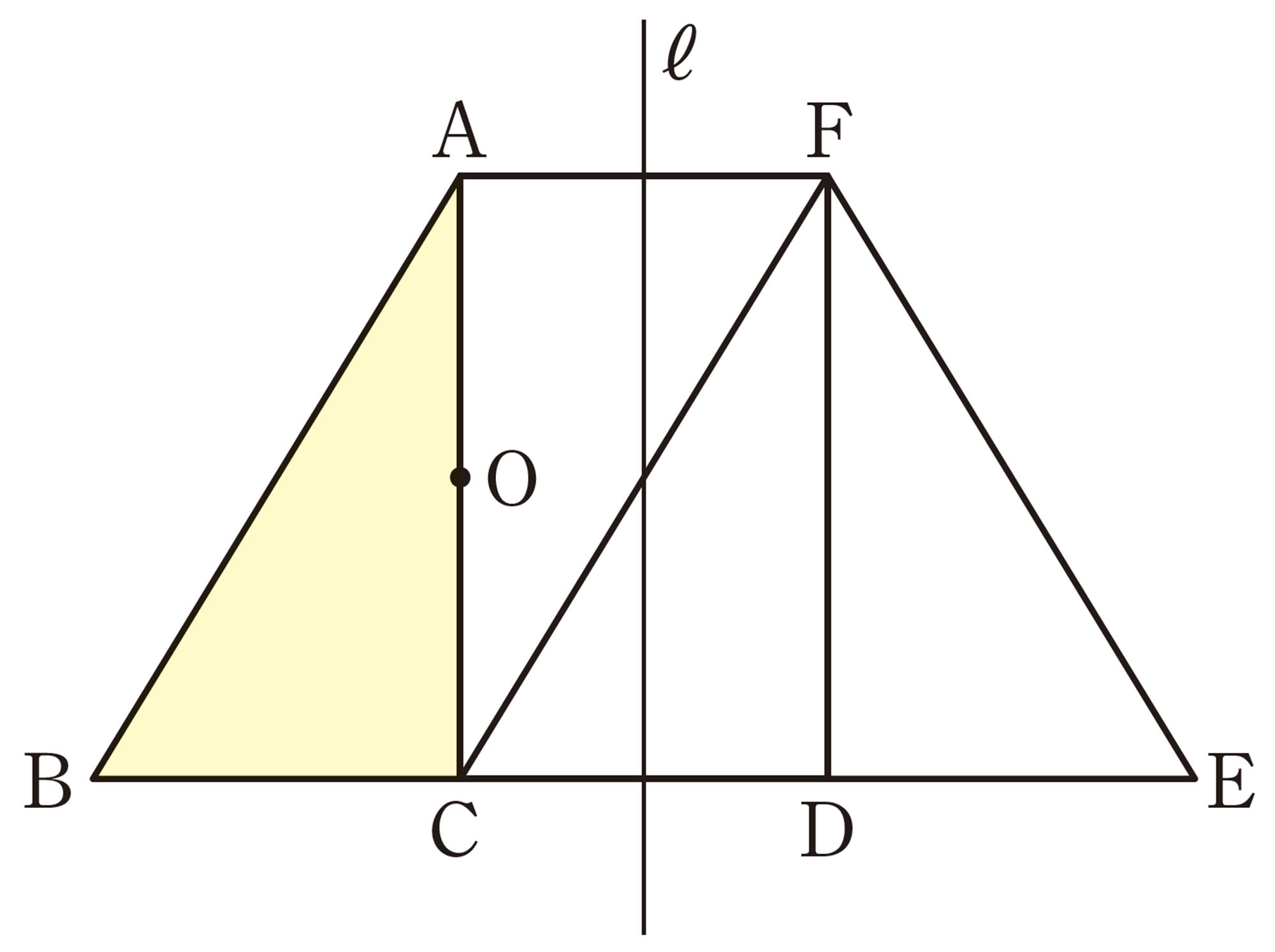
４ 右の図は，合同な4つの直角三角形をすき間なく並べたものです。点 O を線分 ACの中点，直線 ℓ を線分 CDの垂直二等分線とするとき，次の⑴～⑶の移動のしかたを説明しなさい。
⑴ [mathjax]\(\triangle ABC\)を1回の移動で[mathjax]\(\triangle CFA\)に重ねる。
⑵ [mathjax]\(\triangle ABC\)を1回の移動で[mathjax]\(\triangle FED\)に重ねる。
⑶ [mathjax]\(\triangle ABC\)を2回の移動で[mathjax]\(\triangle FED\)に重ねる。
応用
１ 次の大きさの角を作図しなさい。
⑴ [mathjax]\(15^{\circ}\)
⑵ [mathjax]\(135^{\circ}\)
⑶ [mathjax]\(105^{\circ}\)
２ 右の図で，点Aは円Oの円周上の点です。4つの頂点がすべて円Oの円周上にある正方形 ABCDを作図しなさい。
３ 右の図で，[mathjax]\(\triangle ABC\)を1回の回転移動で[mathjax]\(\triangle DEF\)に移動することができます。このとき，回転の中心Oを作図によって求めなさい。
<1年p.200>
5章のまとめの問題 活用
⑴
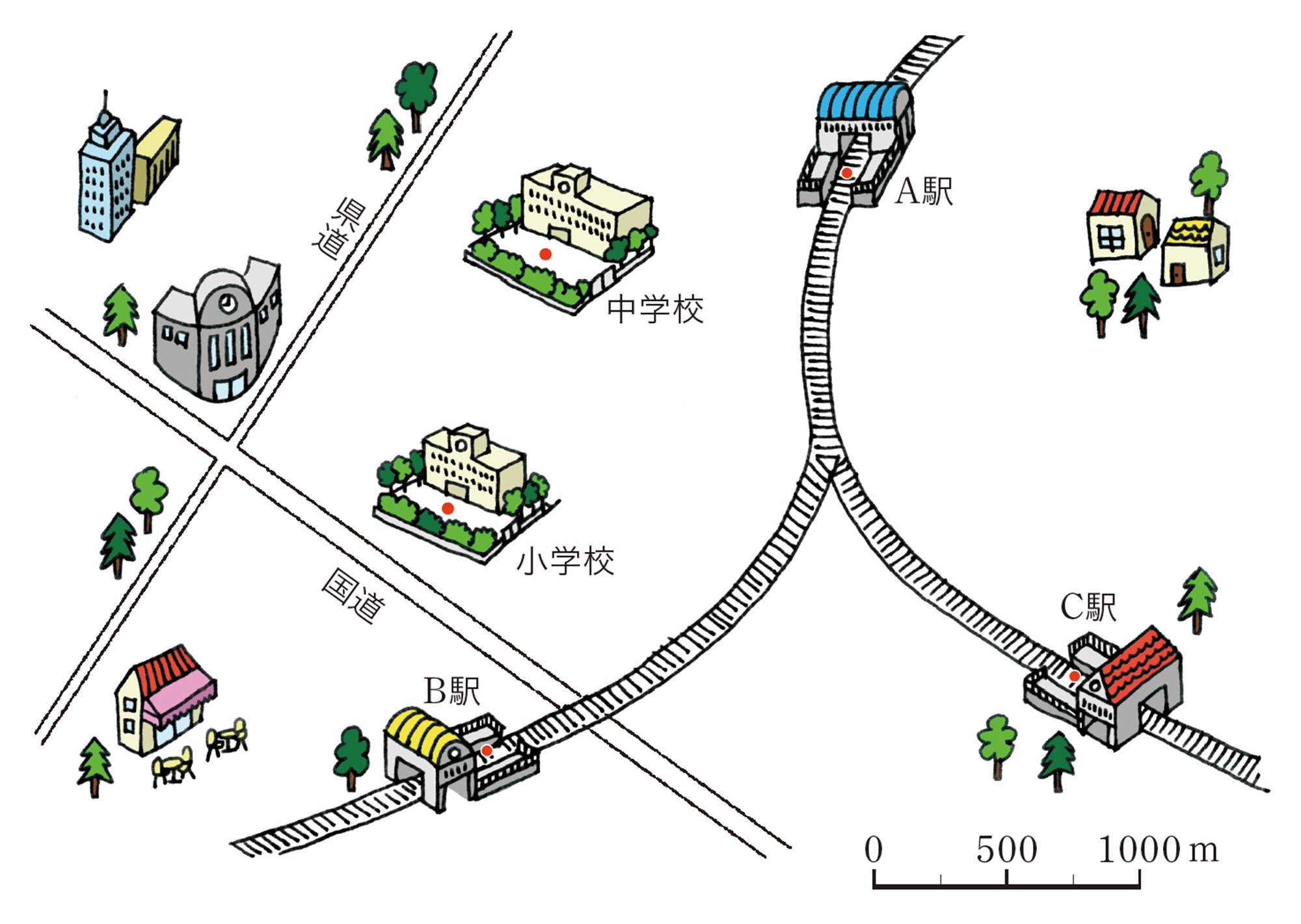
真央「私の家は，A，B，C の3つの駅から等しい距離にあるよ。」
美月「真央さんの家が，2 つの駅から等しい距離にあるなら，2 つの駅を結ぶ線分の垂直二等分線上にあることがわかるね。3 つの駅の場合でも，そのことが利用できるね。」
真央さんの家の位置を作図によって求め，上の地図上に示しなさい。
⑵
美月「私の家は，国道と県道から等しい距離にあって，中学校からは750m 離れているよ。」
真央「角の二等分線を使えば，美月さんの家の位置が求められるね。」
美月さんの家の位置は，2通りの可能性があります。ほかにどんな条件を加えれば1 通りに決まりますか。その例を1つあげなさい。
<1年p.201>
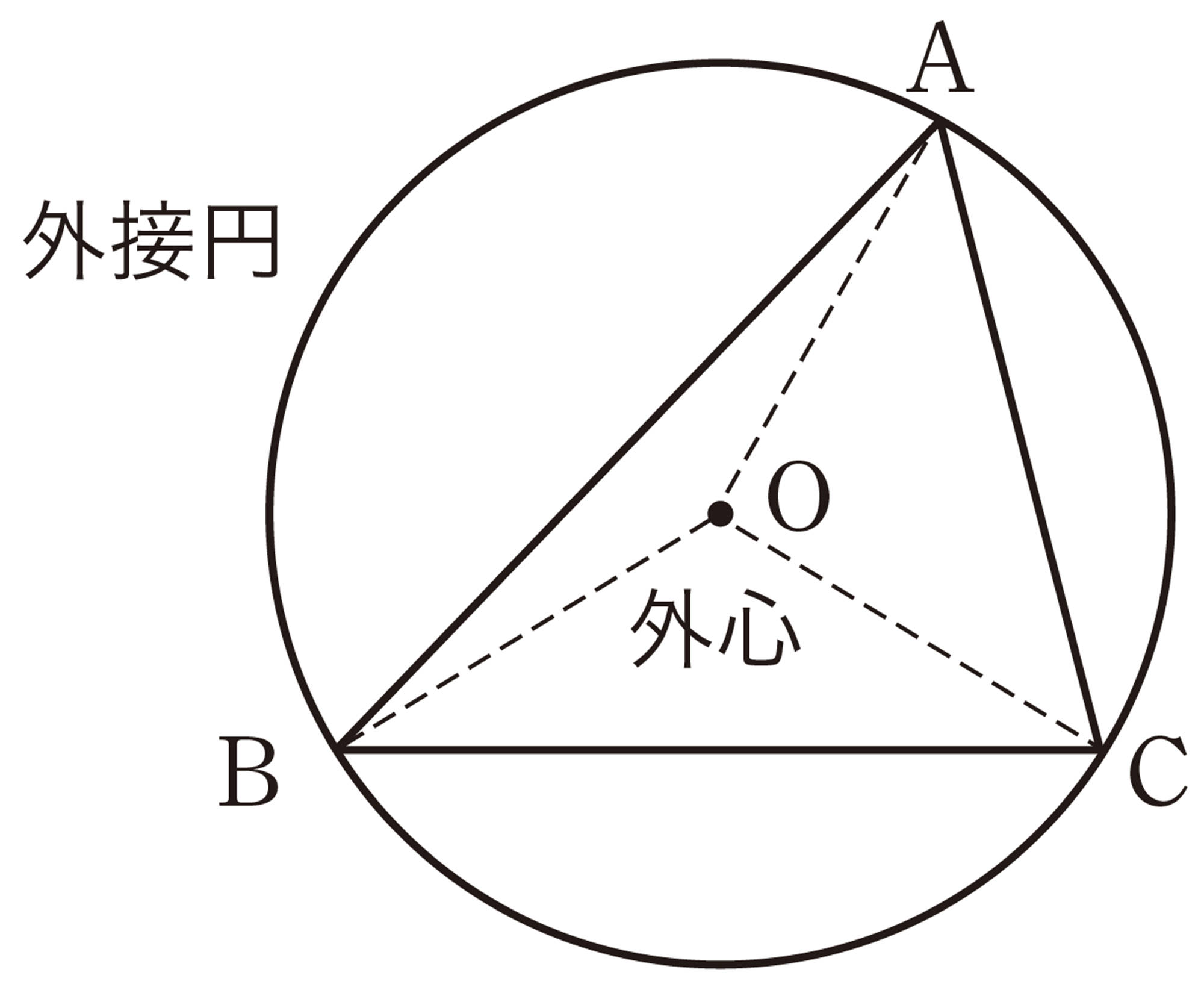
深めよう 発展 高等学校 三角形に接する円を作図しよう
線分の垂直二等分線の作図をもとに，三角形と円の関係を調べてみましょう。
❶ 次の手順で三角形と円を作図してみましょう。
① 3辺の長さを自由に決めて，[mathjax]\(\triangle ABC\)をかく。
② 辺AB，ACの垂直二等分線をそれぞれ引き，交点をOとする。
③ 点Oを中心として，半径OAの円をかく。
❶でかいた円は，[mathjax]\(\triangle ABC\)の3つの頂点を通ります。このような円を[mathjax]\(\triangle ABC\)の外接円といいます。
また，外接円の中心Oを，[mathjax]\(\triangle ABC\)の外心といいます。
❷ ❶でかいた円が，[mathjax]\(\triangle ABC\)の3つの頂点を通る理由を，次の順に説明してみましょう。
① [mathjax]\(OA=OB\)となるのはなぜか。
② [mathjax]\(OA=OC\)となるのはなぜか。
③ 円Oが，3つの頂点A，B，Cを通るのはなぜか。
垂直二等分線の性質を使って説明できるね。
❸ ❶の[mathjax]\(\triangle ABC\)で，辺BCの垂直二等分線を引き，外心Oを通ることを確かめてみましょう。
❹ いろいろな三角形をかき，外心の位置を調べてみましょう。
<1年p.202>
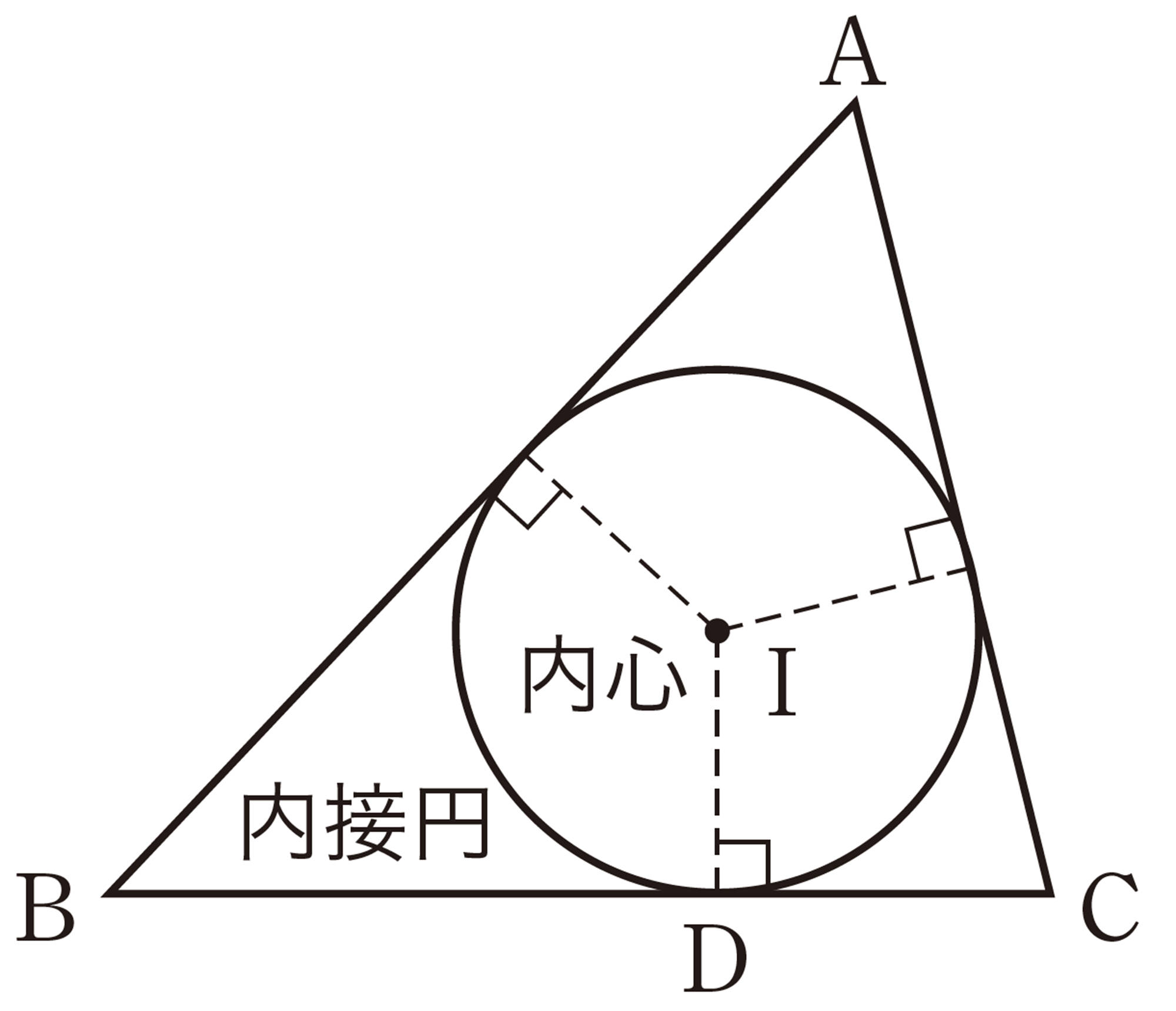
深めよう 三角形に接する円を作図しよう
次に，角の二等分線の作図をもとに，三角形と円の関係を調べてみましょう。
❺ 次の手順で三角形と円を作図してみましょう。
① 3 辺の長さを自由に決めて，[mathjax]\(\triangle ABC\) をかく。
② [mathjax]\(\angle A\)，[mathjax]\(\angle B\) の二等分線をそれぞれ引き，交点をIとする。
③ 点Iから辺BCに垂線を引き，辺BC との交点をDとする。
④ 点Iを中心として，半径IDの円をかく。
❺でかいた円は，[mathjax]\(\triangle ABC\) の3 つの辺に接しています。このような円を，[mathjax]\(\triangle ABC\)の内接円といいます。
また，内接円の中心I を，[mathjax]\(\triangle ABC\)の内心といいます。
❻ ❺でかいた円が[mathjax]\(\triangle ABC\) の3 つの辺に接する理由を，角の二等分線の性質を使って説明してみましょう。
❼ ❺の[mathjax]\(\triangle ABC\)で，[mathjax]\(\angle C\)の二等分線が点Iを通ることを確かめてみましょう。
三角形には，外心と内心をふくめ，「心」と名のつく特定の点が次のように5 種類あります。
外心，内心，重心，傍心，垂心
これらをまとめて「三角形の五心」といいます。
インターネットなどを利用して，三角形の五心について調べてみましょう。
三角形の重心はどこにあるのかな？
