<1年p.191>
2節 図形の移動
ぴったり重ねるには？
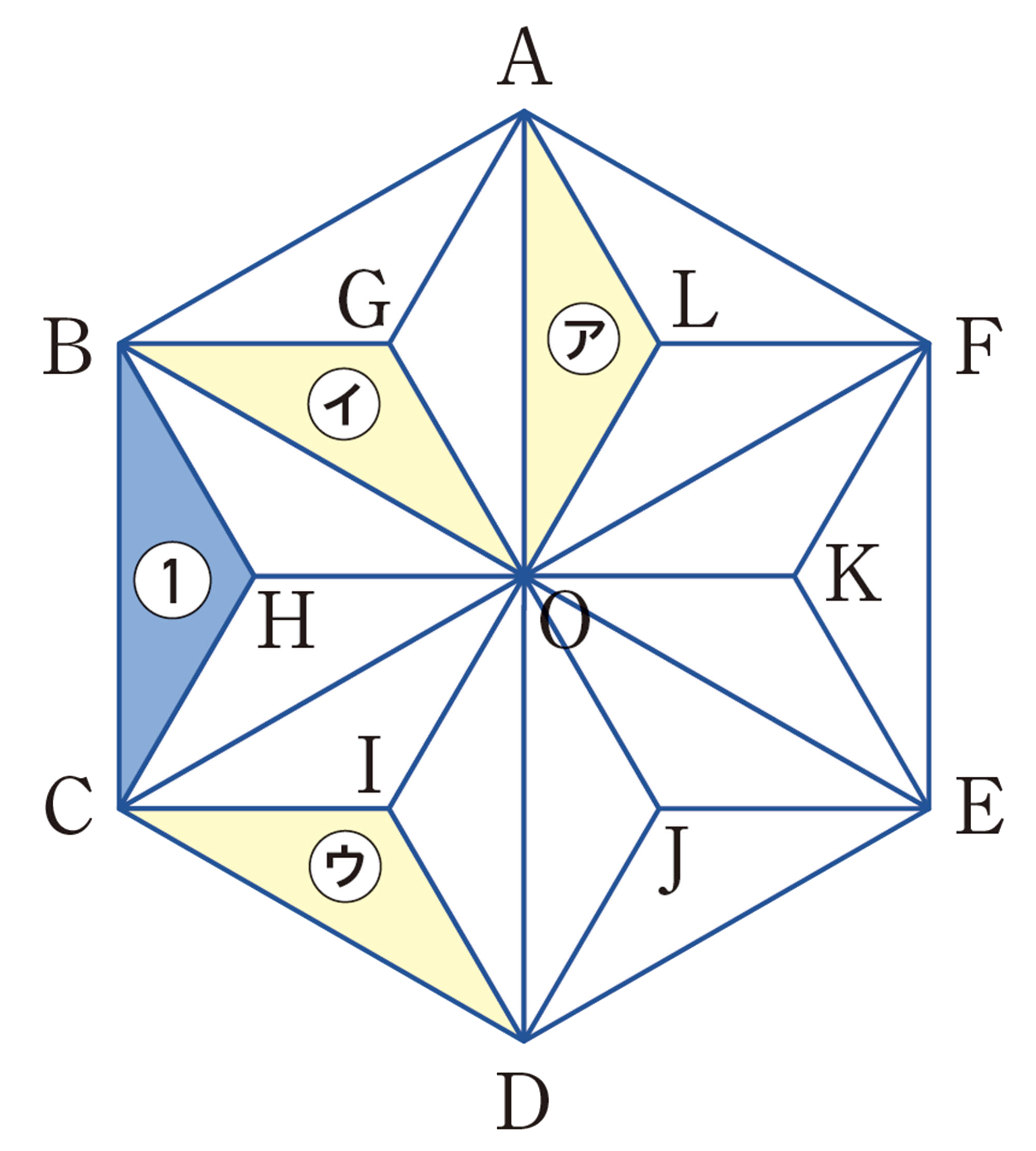
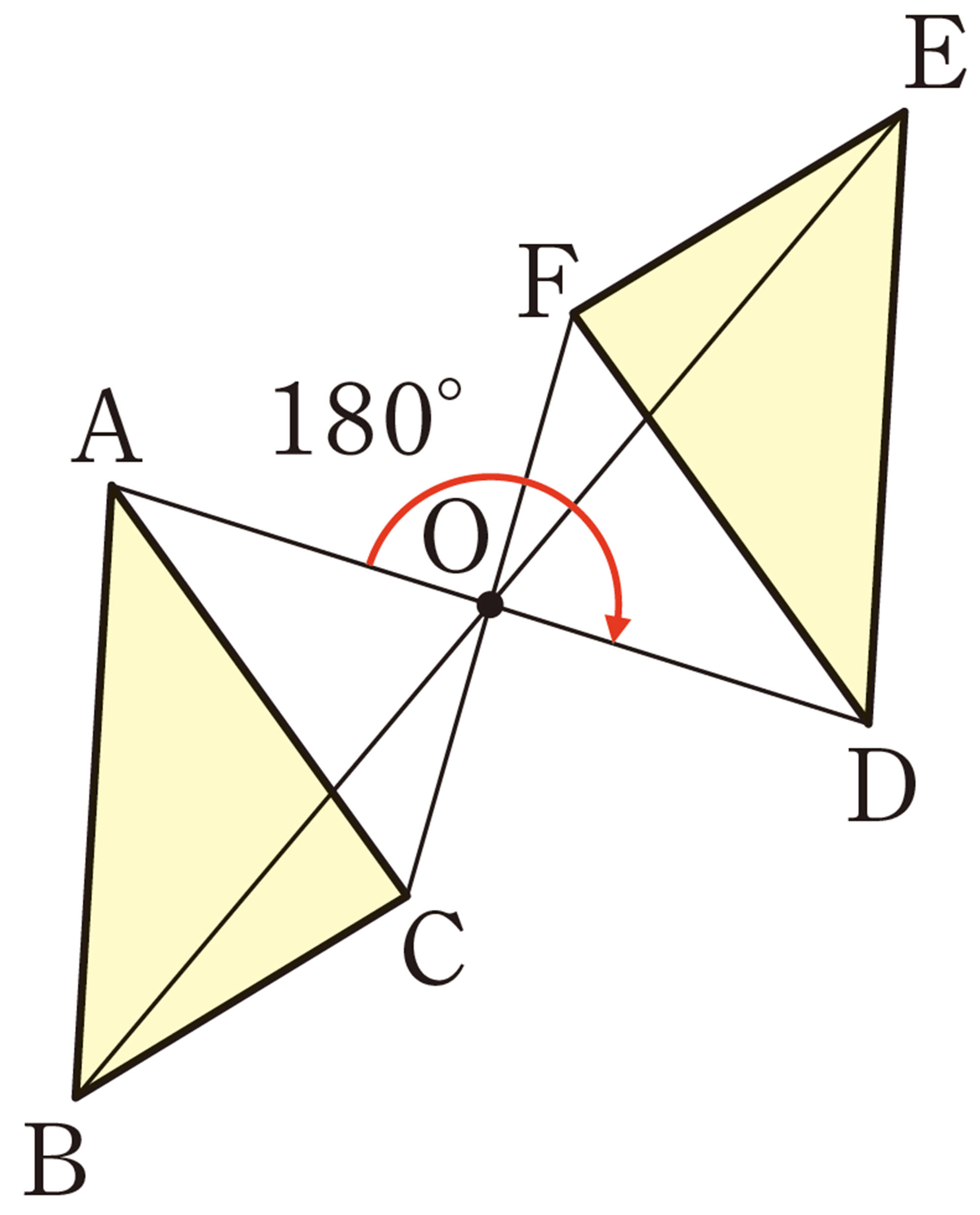
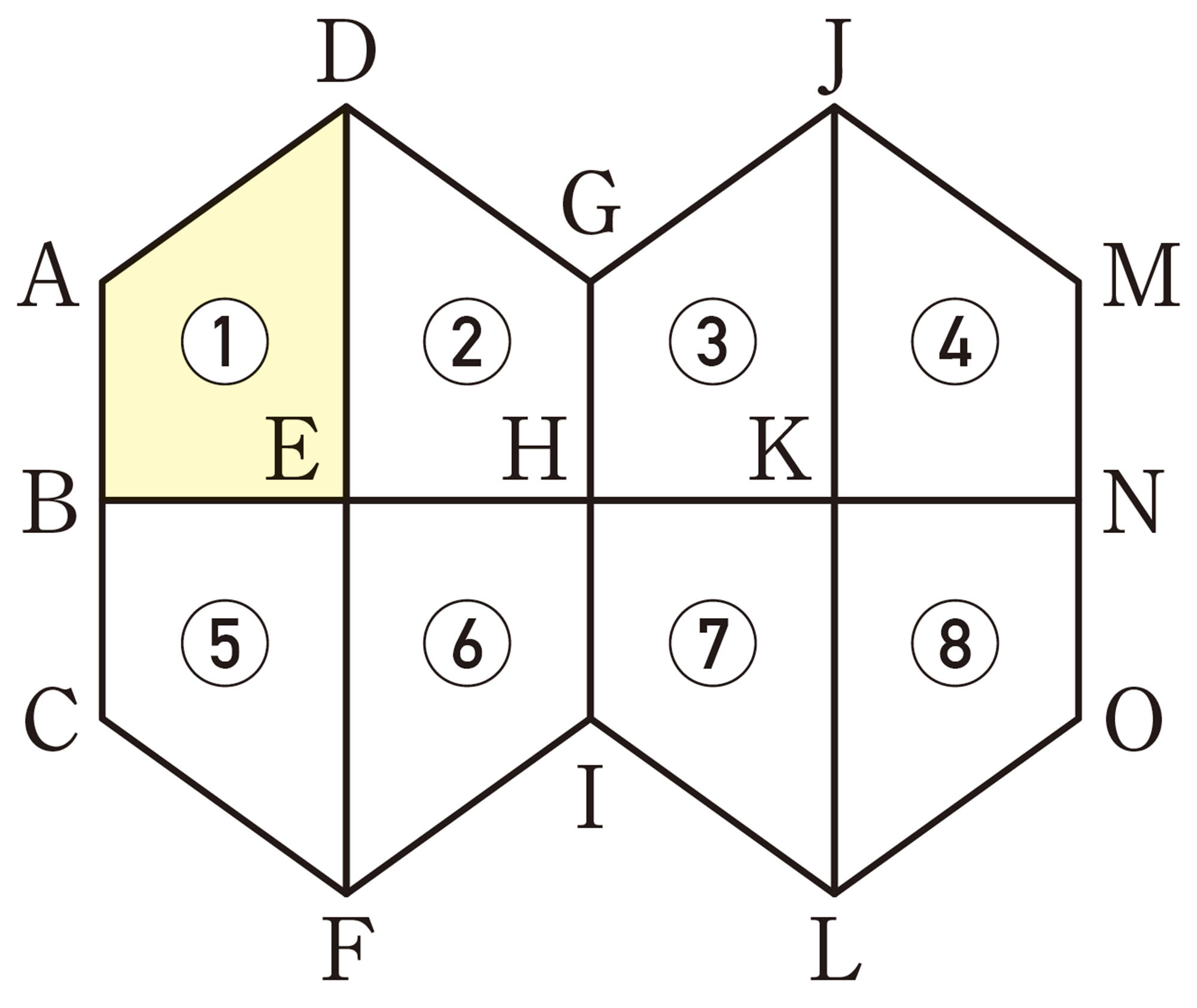
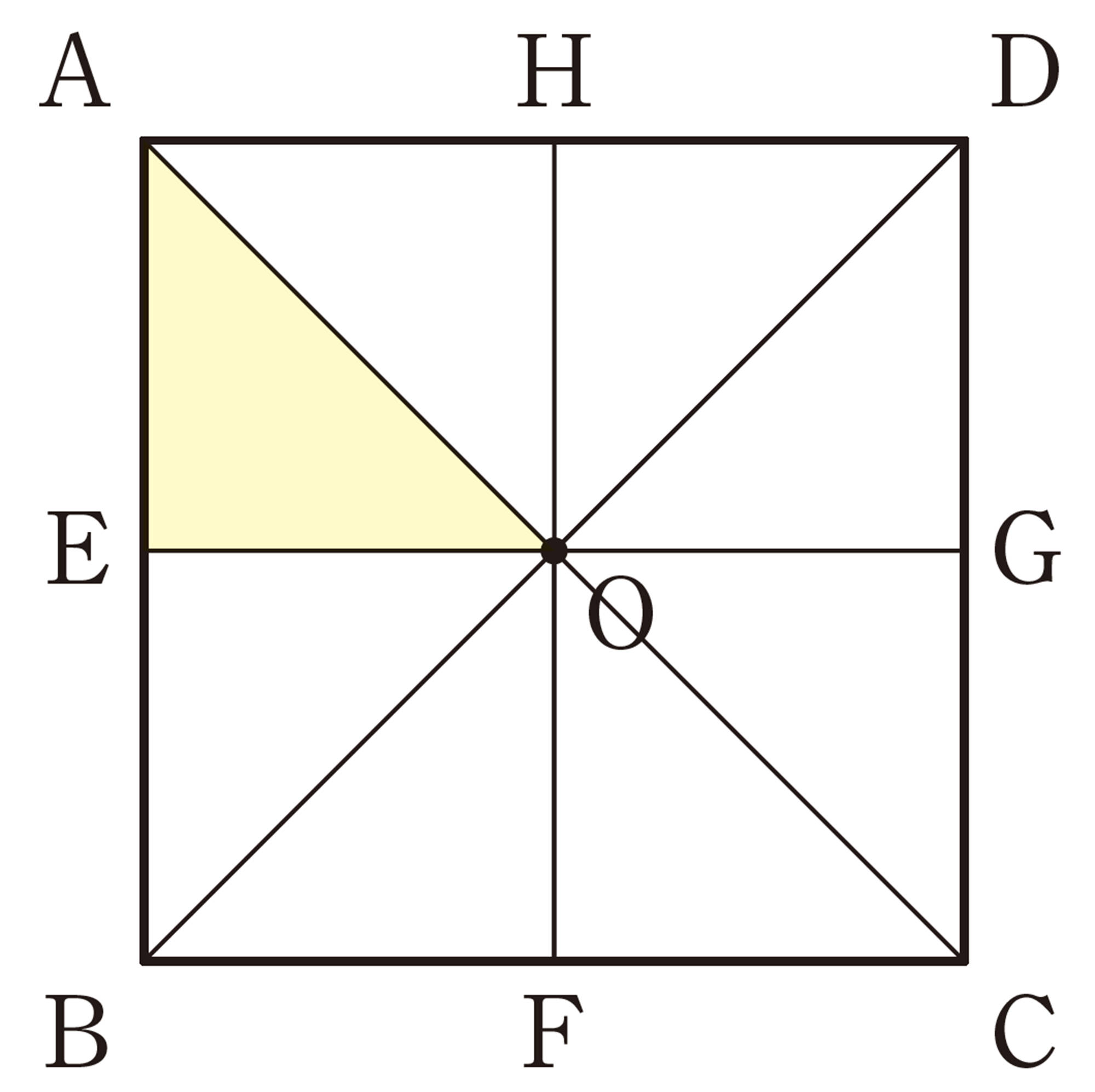
次の図は，「麻の葉」と呼ばれる日本の伝統的な文様です。
【１】 上の文様の中から，いろいろな図形を探しましょう。
二等辺三角形だけでなく，いろいろな図形があるね。
【２】 右の図は「麻の葉」の一部分です。①の二等辺三角形を，㋐ ，㋑ ，㋒ にぴったり重ねるには，それぞれどのように動かせばよいでしょうか。
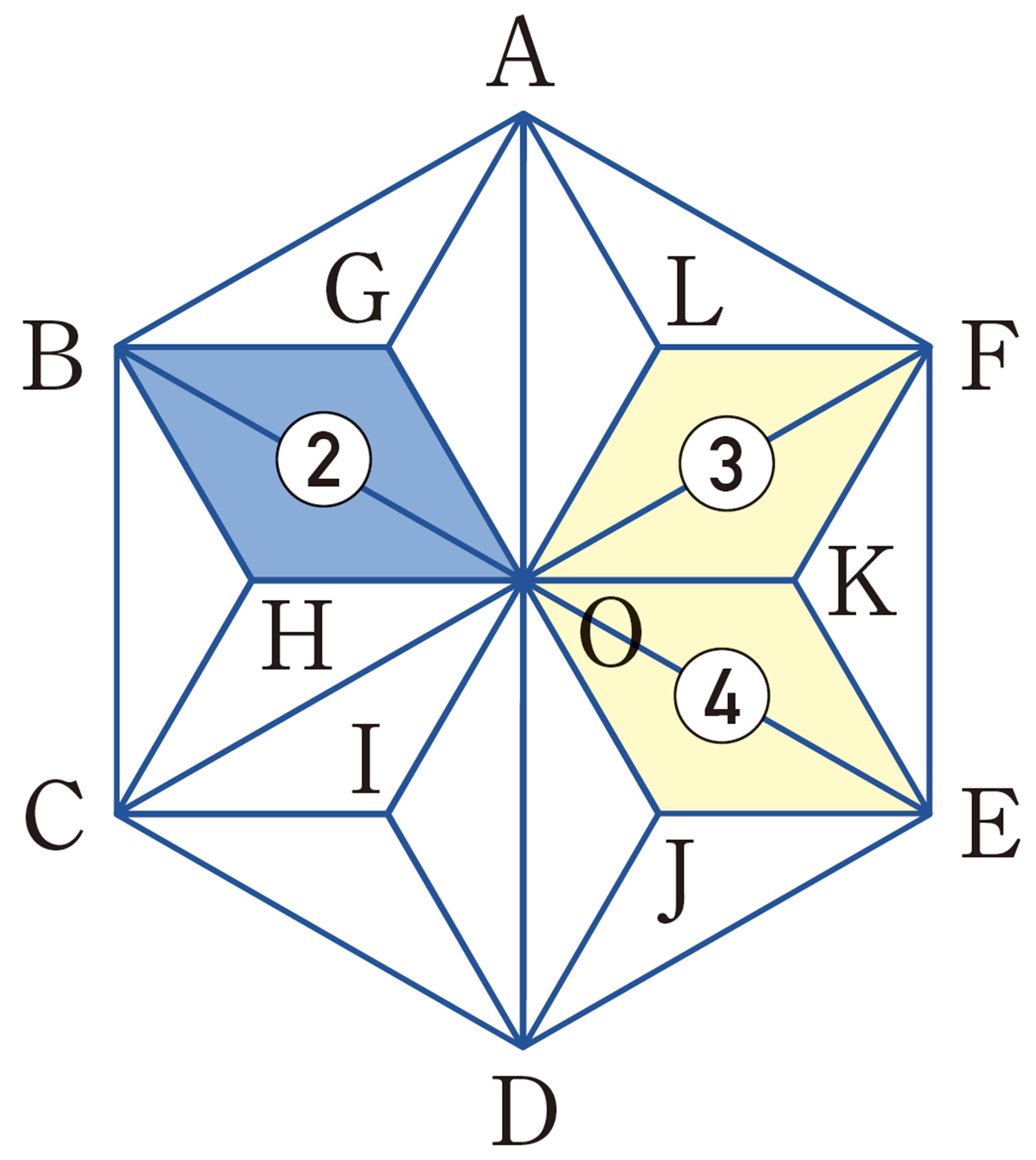
【３】 2の図で，[mathjax]\(\triangle OBC\)を[mathjax]\(\triangle OEF\)にぴったり重ねるには，どのように動かせばよいかを考えてみましょう。
図形の形や大きさを変えずに，図形の位置だけを変えることを，図形の 移動 という。
次の課題へ！
図形の移動には，どんな方法があるのかな？
P.192
<1年p.192>
１ 図形の移動
目標 ▷ 図形の移動について調べよう。
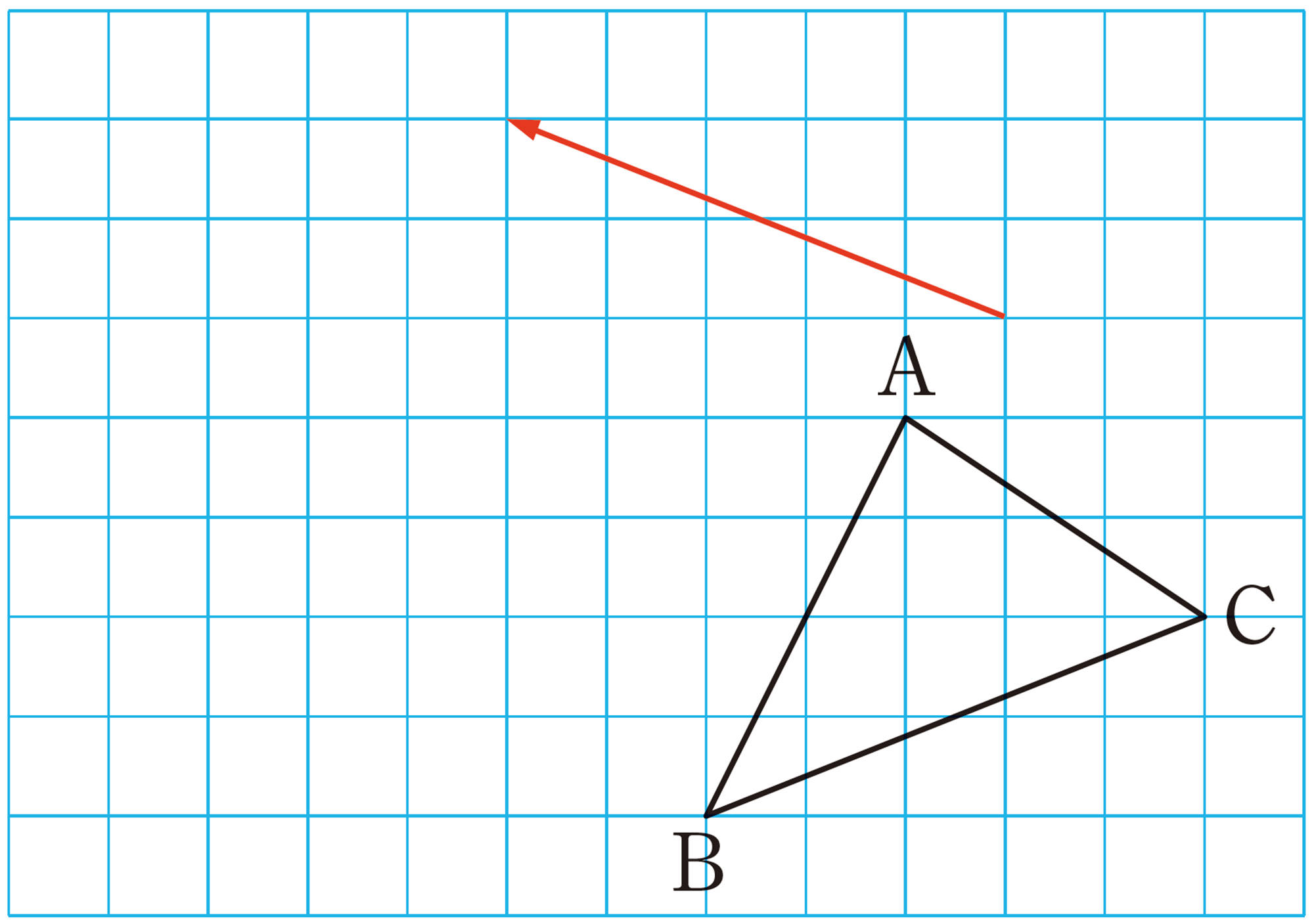
平行移動
例 １ 右の図で，[mathjax]\(\triangle DEF\)は，[mathjax]\(\triangle ABC\) を，矢印の方向に矢印の長さだけ移動した図形である。
図形を，一定の方向に一定の距離だけずらす移動を 平行移動 という。
平行移動では，図形の各点を同じ方向に同じ距離だけ動かすから，例1において，次の関係が成り立つ。
[mathjax]\(AD/\!/BE/\!/CF\)
[mathjax]\(AD=BE=CF\)
注意 [mathjax]\(AD /\!/BE/\!/CF\)は，AD，BE，CF がたがいに平行であることを表している。
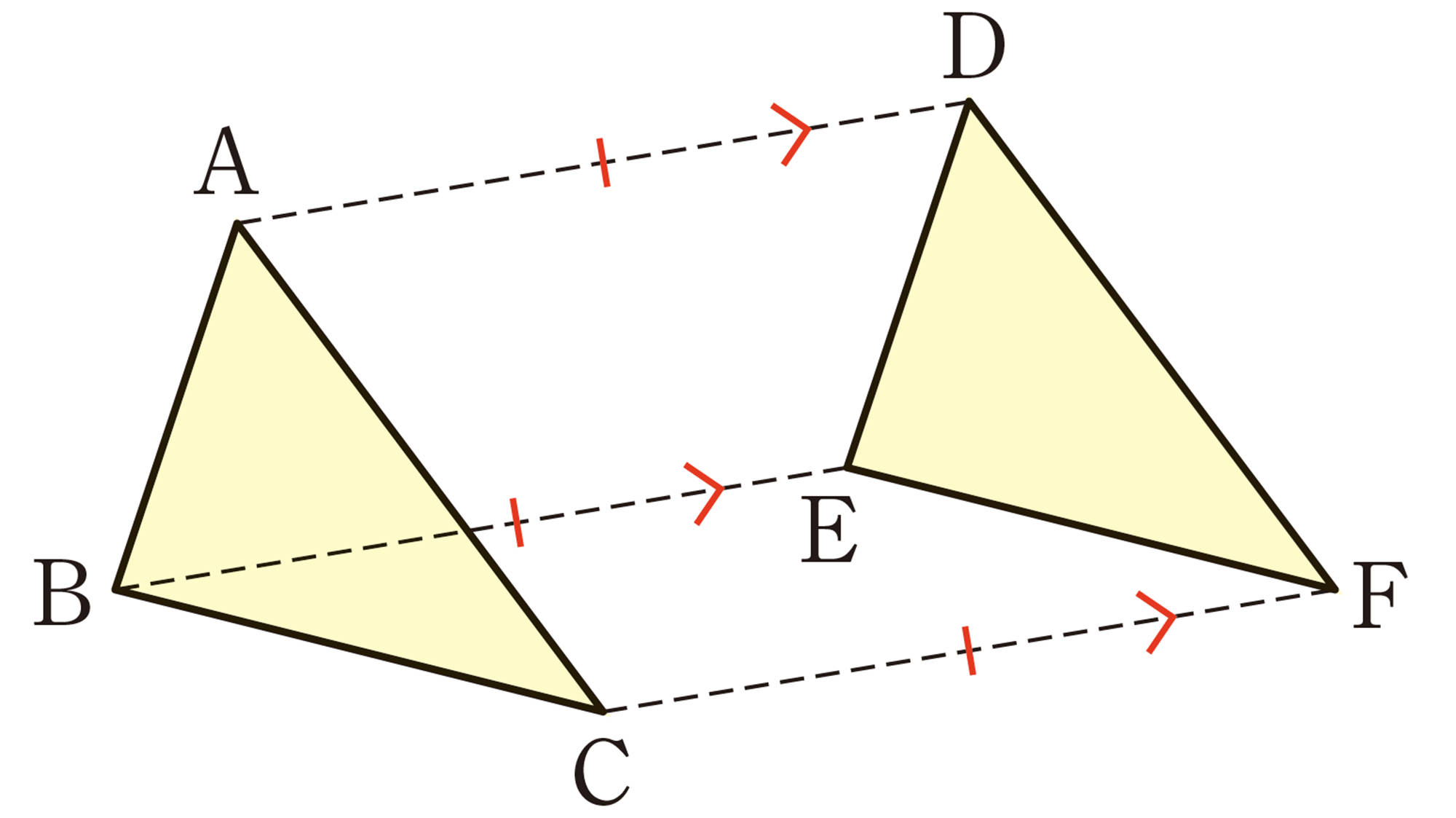
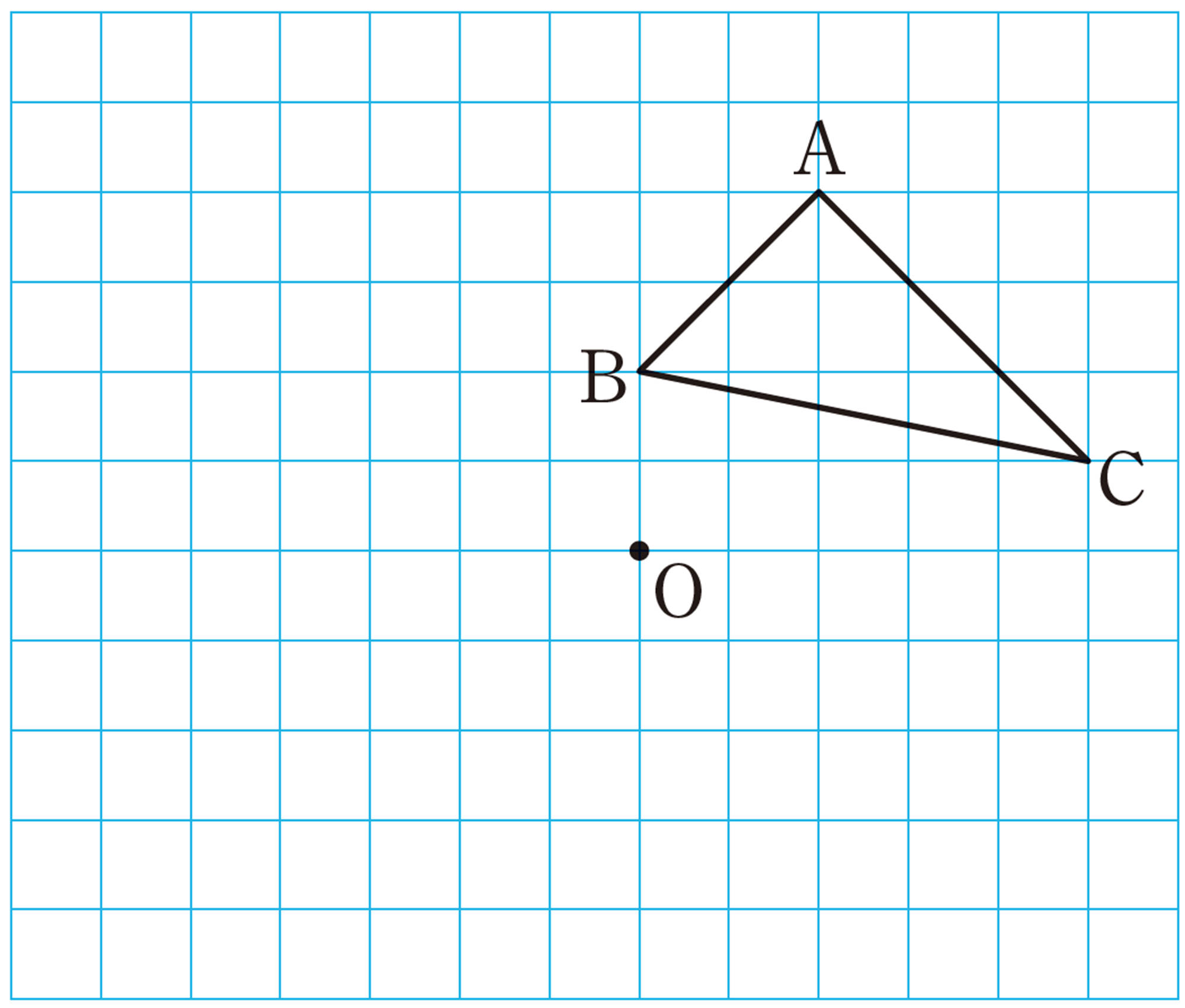
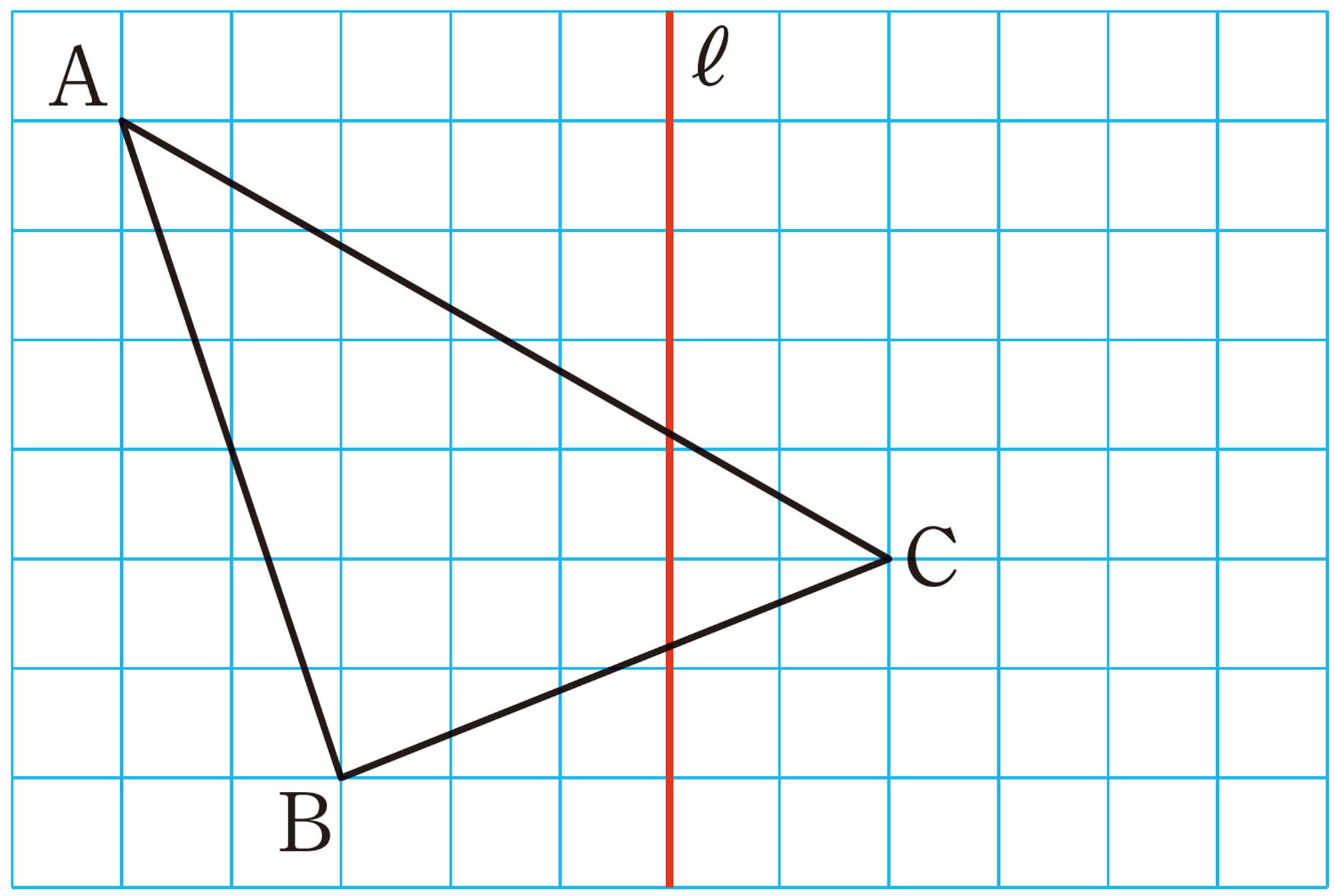
問 １ 例1の[mathjax]\(\triangle ABC\)と[mathjax]\(\triangle DEF\)について，次の問いに答えなさい。
⑴ 対応する辺ABとDE，BCとEF，CAとFDの間には，それぞれどんな関係がありますか。
⑵ 対応する角[mathjax]\(\angle A\) と[mathjax]\(\angle D\)，[mathjax]\(\angle B\) と[mathjax]\(\angle E\)，[mathjax]\(\angle C\)と[mathjax]\(\angle F\)の間には，それぞれどんな関係がありますか。
問 ２
左の図で，[mathjax]\(\triangle ABC\)を，矢印の方向に矢印の長さだけ平行移動した[mathjax]\(\triangle DEF\)をかきなさい。
<1年p.193>
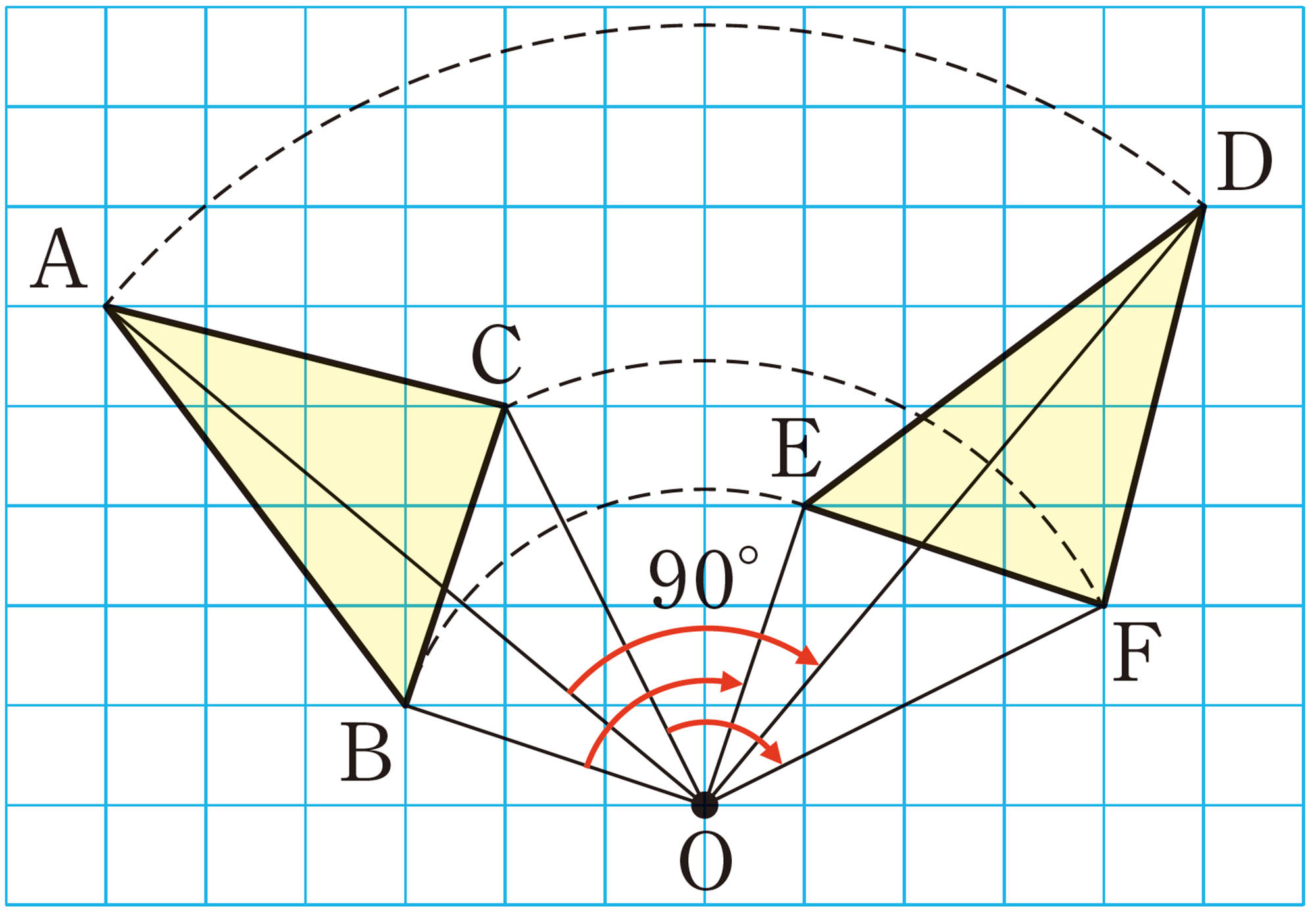
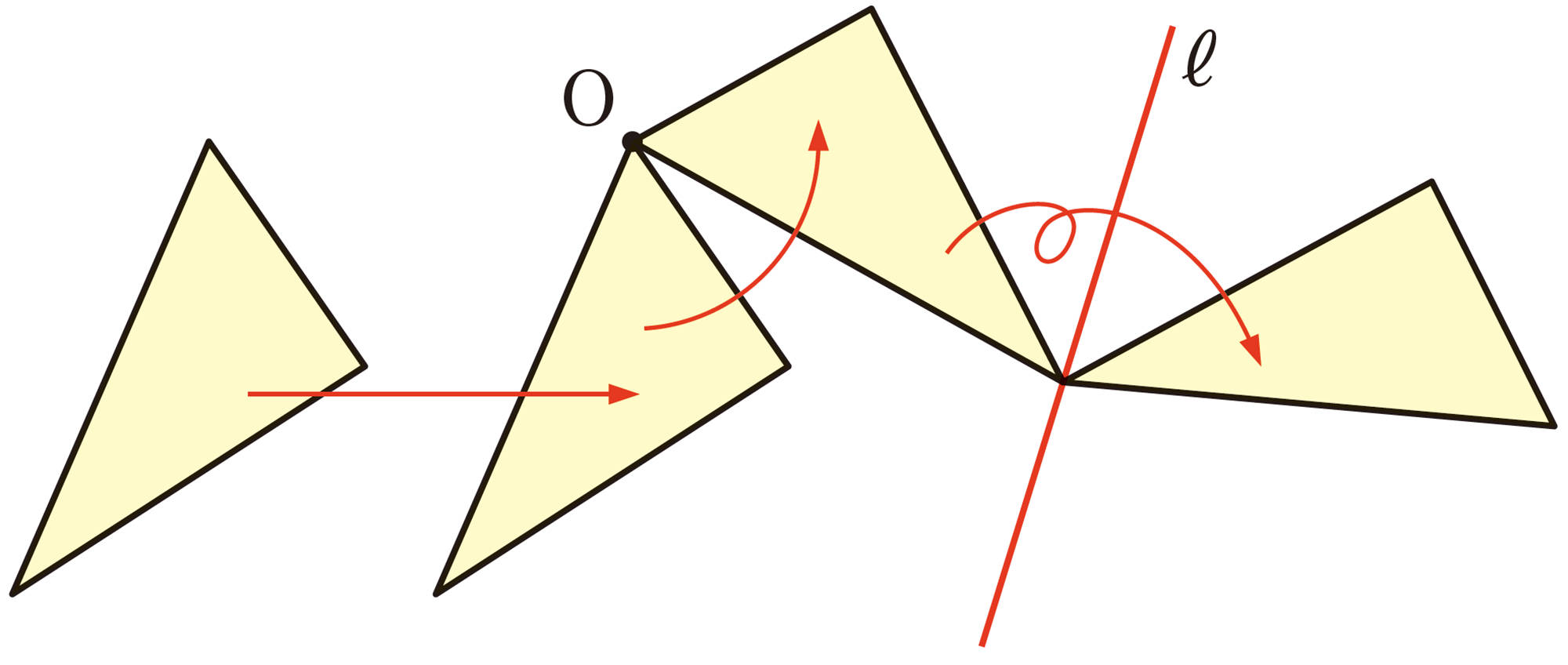
回転移動
例 ２ 右の図で，[mathjax]\(\triangle DEF\)は，[mathjax]\(\triangle ABC\)を，点Oを中心として時計回りの方向に[mathjax]\(90^{\circ}\)回転した図形である。
図形を，1つの点を中心として一定の角度だけ回転させる移動を回転移動 といい，中心とした点を 回転の中心 という。
回転移動では，図形の各点を同じ方向に同じ角度だけ回転させるから，例2において，次の関係が成り立つ。
[mathjax]\(\angle AOD=\angle BOE=\angle COF=90^{\circ}\)
[mathjax]\(OA=OD\)，[mathjax]\(OB=OE\)，[mathjax]\(OC=OF\)
回転移動のうち，右の図のように，1つの点を中心として[mathjax]\(180^{\circ}\)回転させる移動を，点対称移動 という。
問 ３ 右の図について，次の問いに答えなさい。
⑴ [mathjax]\(\triangle ABC\)を，点Oを回転の中心とし て反時計回りの方向に[mathjax]\(90^{\circ}\)回転移動した[mathjax]\(\triangle DEF\)をかきなさい。
⑵ [mathjax]\(\triangle ABC\)を，点Oを回転の中心として点対称移動した[mathjax]\(\triangle GHI\)をかきなさい。
<1年p.194>
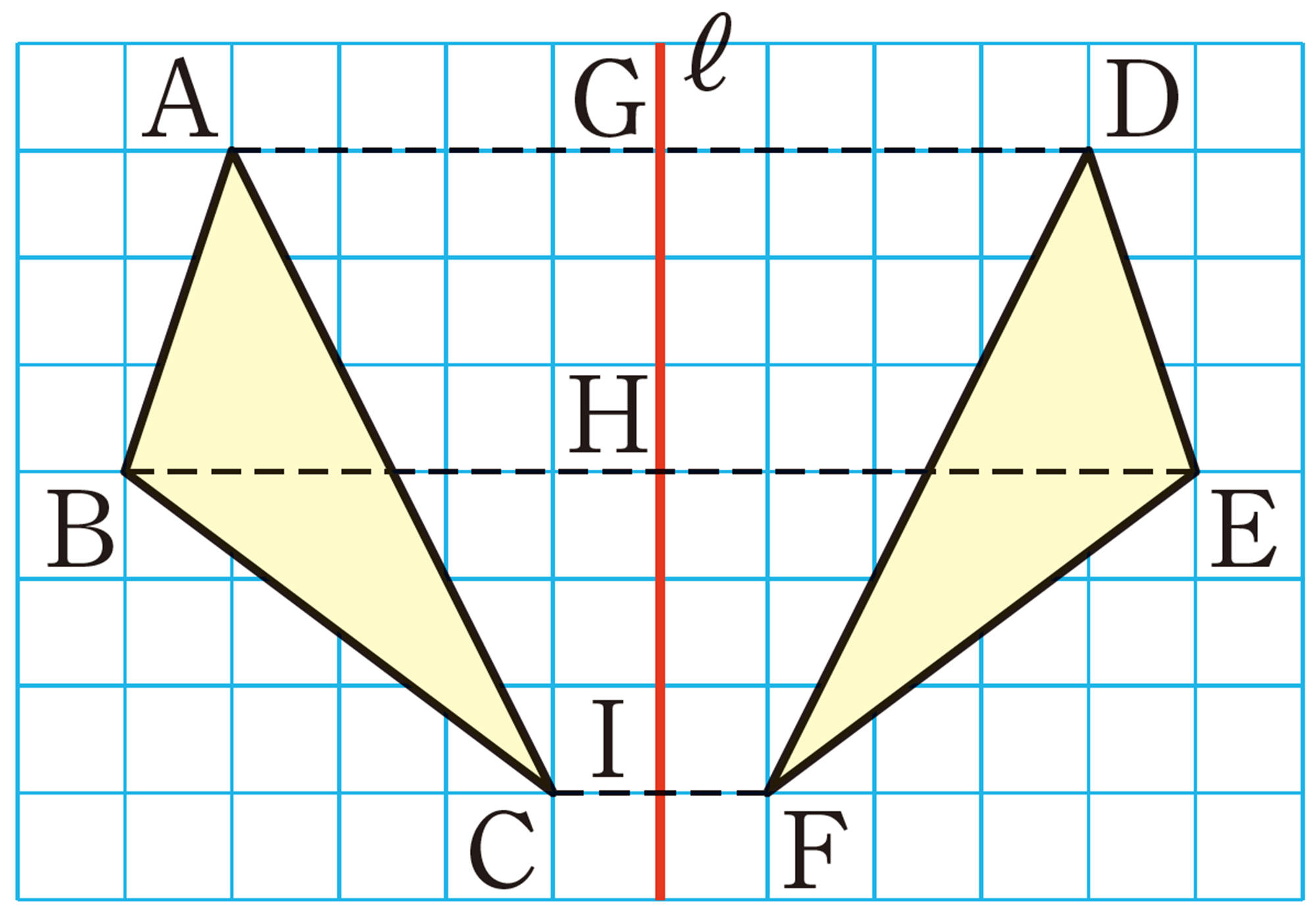
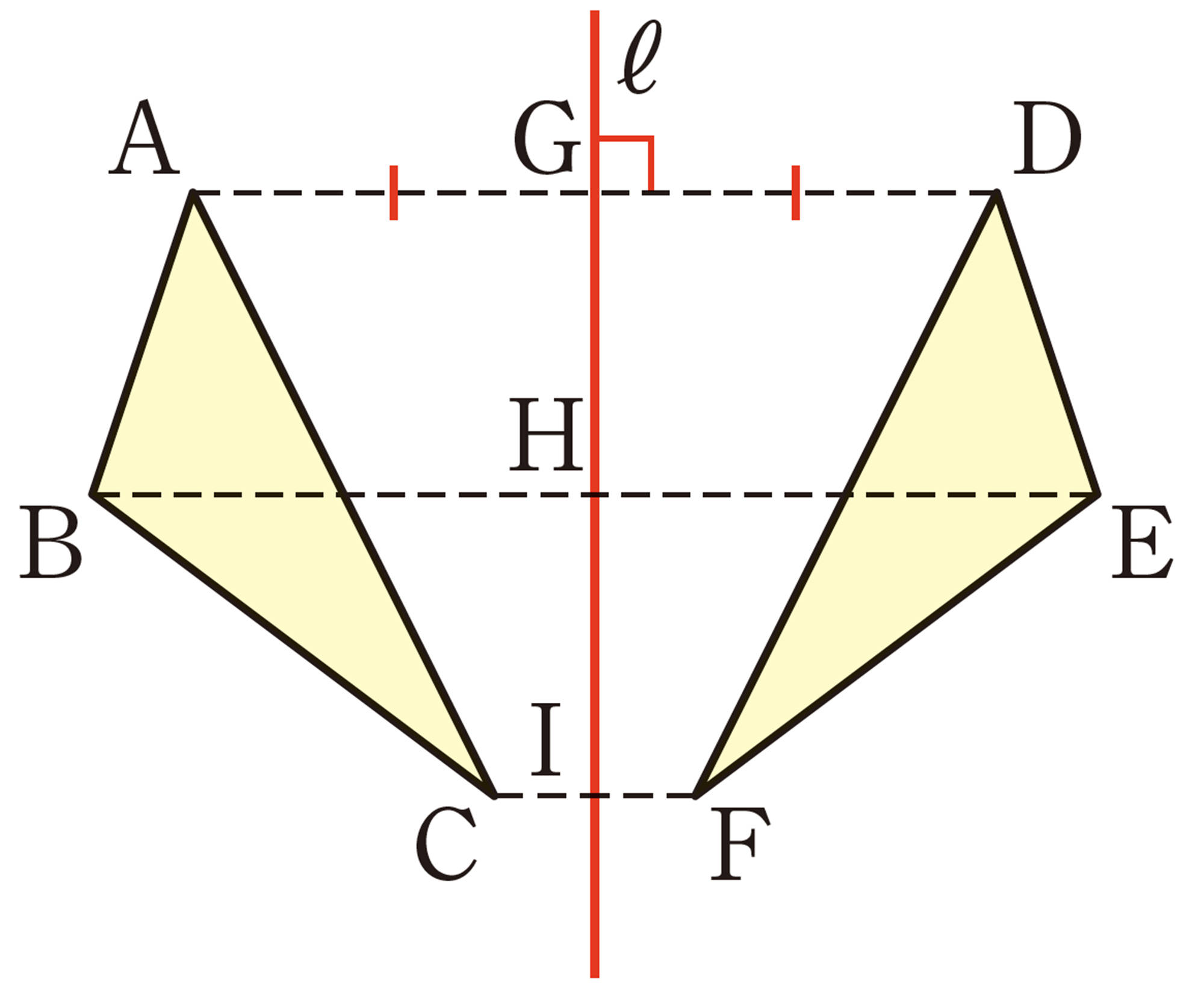
対称移動
例 ３ 右の図で，[mathjax]\(\triangle DEF\)は，[mathjax]\(\triangle ABC\)を，直線 ℓ を折り目として折り返した図形である。
図形を，1つの直線を折り目として折り返す移動を 対称移動 といい，折り目とした直線を 対称の軸 という。
例3において，直線 ℓで折り返したとき，線分AGと線分 DGは重なるから，直線 ℓは線分ADの垂直二等分線である。
したがって，次の関係が成り立つ。
[mathjax]\(ℓ\bot AD\)，[mathjax]\(AG=DG\)
問 ４ 例3の図で，直線 ℓ は，線分 BE，CFと，それぞれどのように交わっていますか。記号を使って表しなさい。
問 ５
左の図で，[mathjax]\(\triangle ABC\)を，直線 ℓ を対称の軸として対称移動した[mathjax]\(\triangle DEF\)をかきなさい。
平行移動，回転移動，対称移動した図形はもとの図形と合同である。
これらの移動を組み合わせると，平面図形をいろいろな位置に移動することができる。
<1年p.195>
問 ６ 191ページの 2の図について，次の問いに答えなさい。
⑴ [mathjax]\(\triangle OBC\)を，点Oを中心として時計回りの方向に何度回転移動させると，[mathjax]\(\triangle ODE\)に重なりますか。
⑵ 四角形OABCを，点Oを中心として反時計回りの方向に[mathjax]\(120^{\circ}\)回転させると，どの図形に重なりますか。
⑶ ②を③に重ねるには，どんな移動をすればよいですか。大和さんは，次のように説明しました。大和さんの説明について，気づいたことを話し合いなさい。
②を③に重ねるには，② を[mathjax]\(120^{\circ}\)回転させます。
大和さんの説明では，どこを中心として，どちらの方向に回転させるのかがないので，伝わらないと思います。
なるほど，回転移動では，「どこを中心として」，「どちらの方向に」，「何度」の3つの要素を説明しないと，きちんと伝わらないね。
「②を③ に重ねるには，② を点Oを中心として，時計回りの方向に[mathjax]\(120^{\circ}\)回転させます。」という説明になります。
対称移動でも②を③に重ねられます。対称移動を説明するには，どんな要素が必要なのかな。
対称移動については，対称の軸がどれなのかを明確にすればよさそうだね。
⑷ ②を④に重ねるには，どんな移動をすればよいですか。
回転移動，対称移動のほかに，平行移動でもできそうだよ。
平行移動については，どのように説明すればよいのかな。
<1年p.196>
問 ７ 右の図は，8つの合同な台形を，すき間なく並べたものです。次の問いに答えなさい。
⑴ ①を，点Eを回転の中心として回転移動したとき，重なる図形はどれですか。
⑵ ①を，直線DEを対称の軸として対称移動し，さらに直線 EHを対称の軸として対称移動したとき，重なる図形はどれですか。
⑶ ①を，1回の移動で⑧に重ねるためには，どのように移動すればよいですか。
⑷ ①を，2回の移動で⑧に重ねるためには，どのように移動すればよいですか。2通りの方法を答えなさい。
どんなことがわかったかな
図形の移動には，平行移動，回転移動，対称移動があり，これらを組み合わせると，平面図形をいろいろな位置に移動することができます。
確かめよう 2節 図形の移動
１ 正方形の紙を何回か2つ折りにして，右の図のような折り目の線をつけました。 この図について，次の問いに答えなさい。
⑴ [mathjax]\(\triangle AEO\)を平行移動するだけで重なる三角形をいいなさい。
⑵ [mathjax]\(\triangle AEO\)を，点Oを回転の中心として回転移動するだけで重なる三角形をいいなさい。
⑶ [mathjax]\(\triangle AEO\)を対称移動して[mathjax]\(\triangle BEO\)に重ねるとき，対称の軸をいいなさい。
<1年p.197>
5章 「平面図形」を学んで
できるようになったこと 身のまわりの課題へ P.200,289
図形の性質を理解して，作図することができる。
平面上にある合同な図形を，図形の移動という見方でみることができる。
図形の性質を利用したり，作図したりすることで，身のまわりや数学の中から見つけた問題を解決することができる。
さらに学んでみたいこと
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
数学へのいざない ルーローの三角形
右の図は，ルーローの三角形と呼ばれています。これは，中にある正三角形の各頂点を中心として，半径が正三角形の辺の長さになるように弧をかいたものです。
このような図形の仲間は，定幅図形と呼ばれ，転がしたときに高さが変わらない図形です。
ルーローの三角形は，ロボット掃除機や穴をあけるドリルに利用されています。ロボット掃除機は部屋の4すみも掃除することができ，ドリルは正方形に近い形の穴をあけることができます。
