<1年p.181>
2 [mathjax]\(60^{\circ}\),[mathjax]\(30^{\circ}\)の角の作図
Q Question
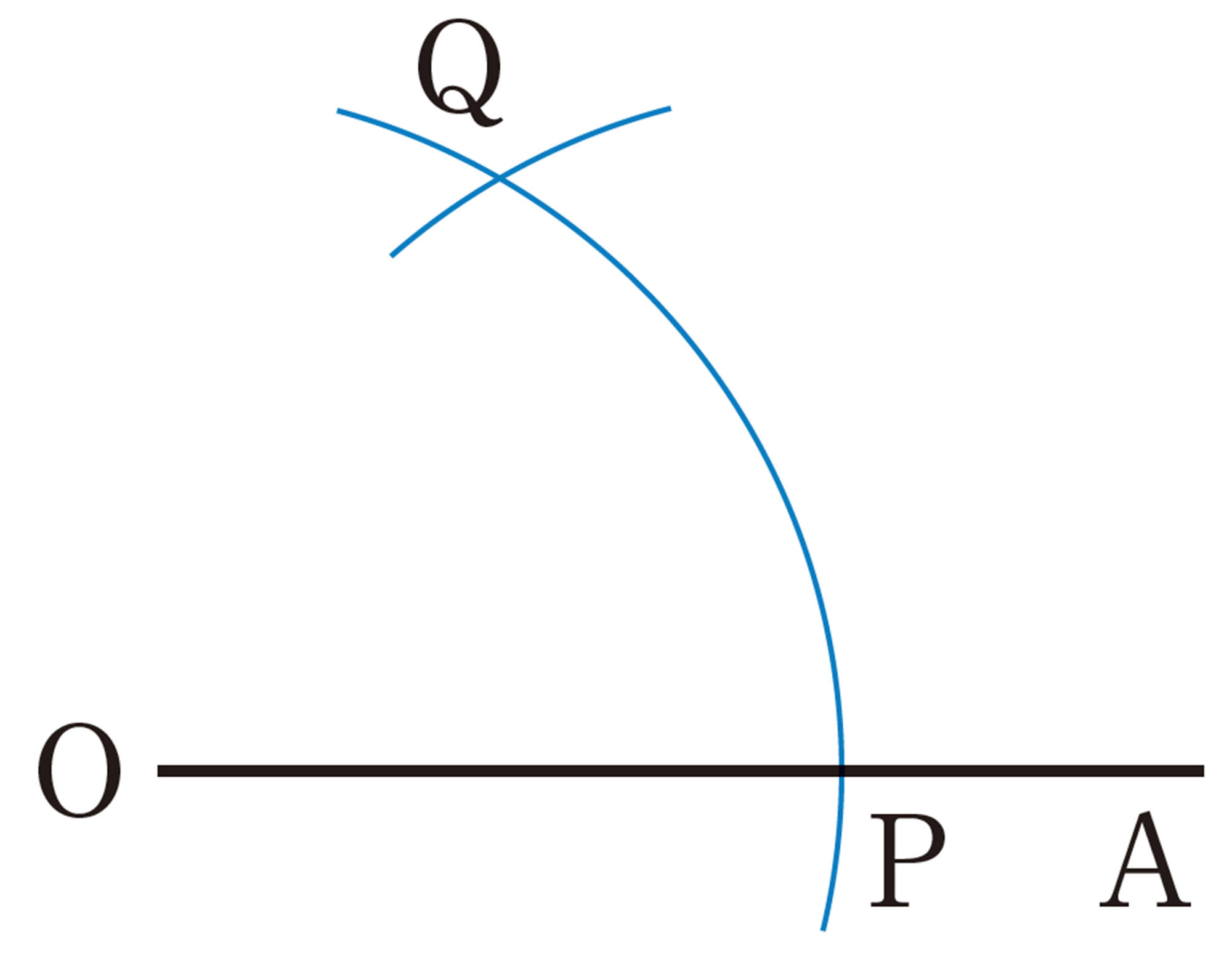
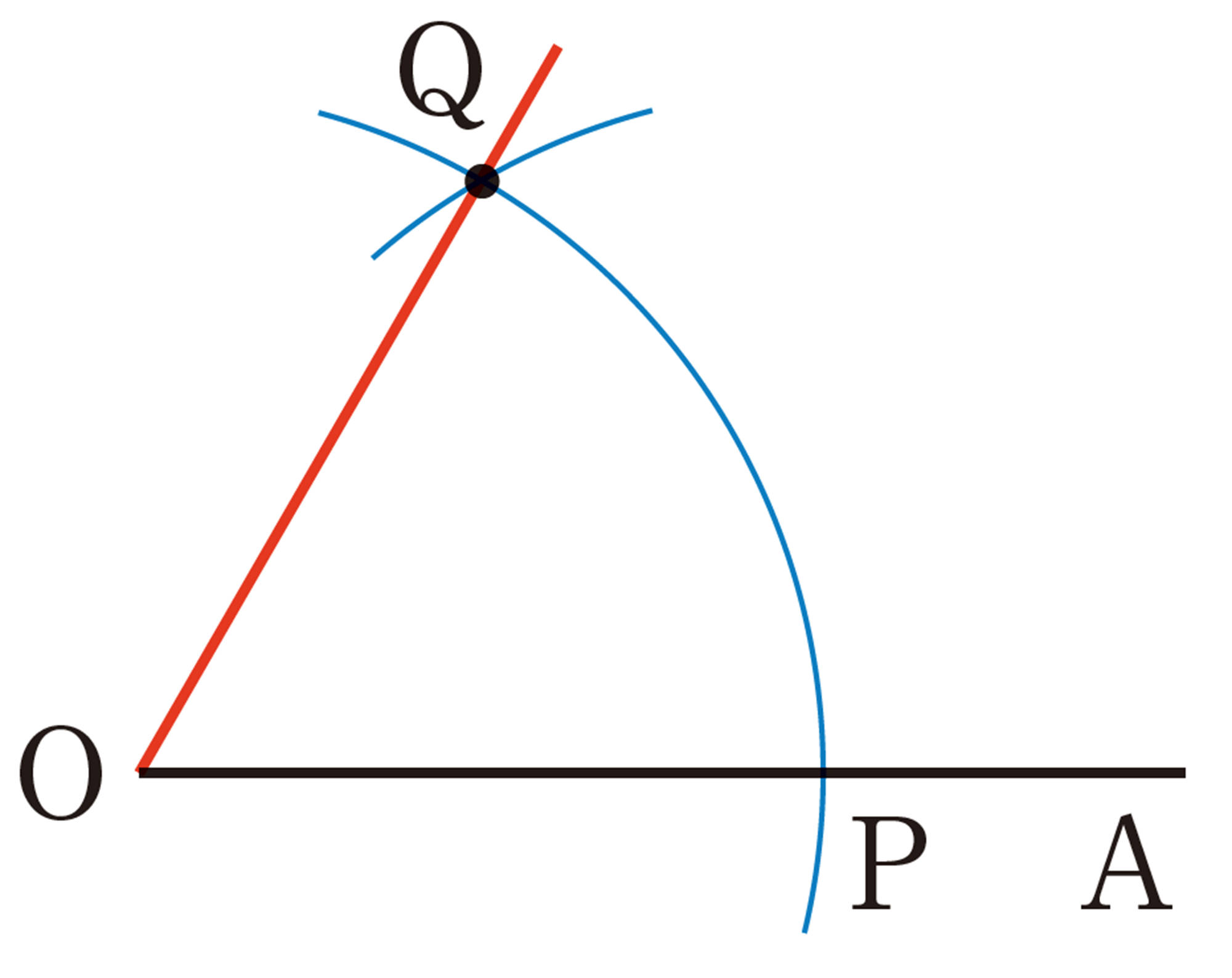
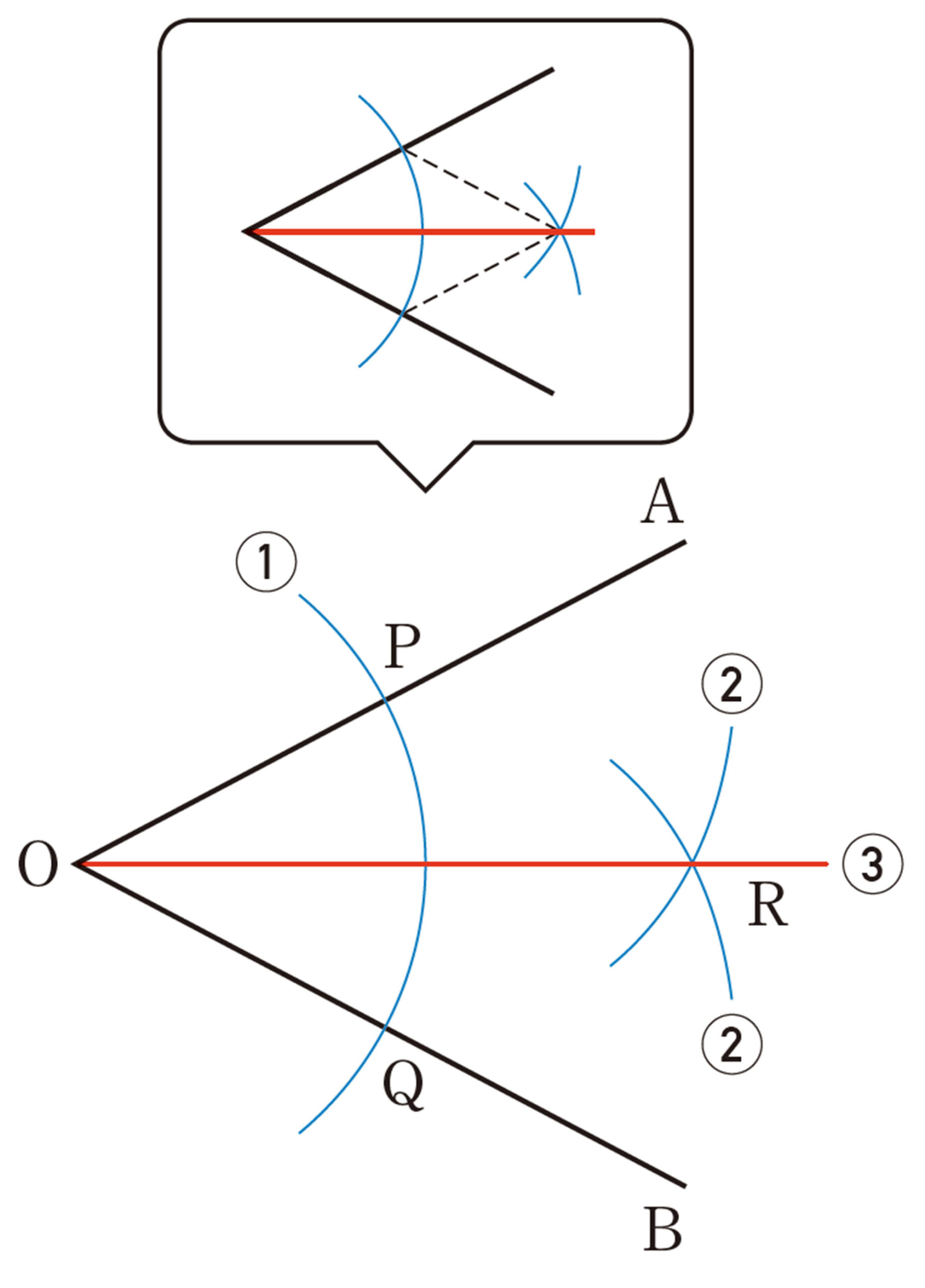
[mathjax]\(60^{\circ}\)の角を作図するには,どのようにすればよいでしょうか。
[mathjax]\(60^{\circ}\)の角の作図に利用できる図形があるか話し合ってみましょう。

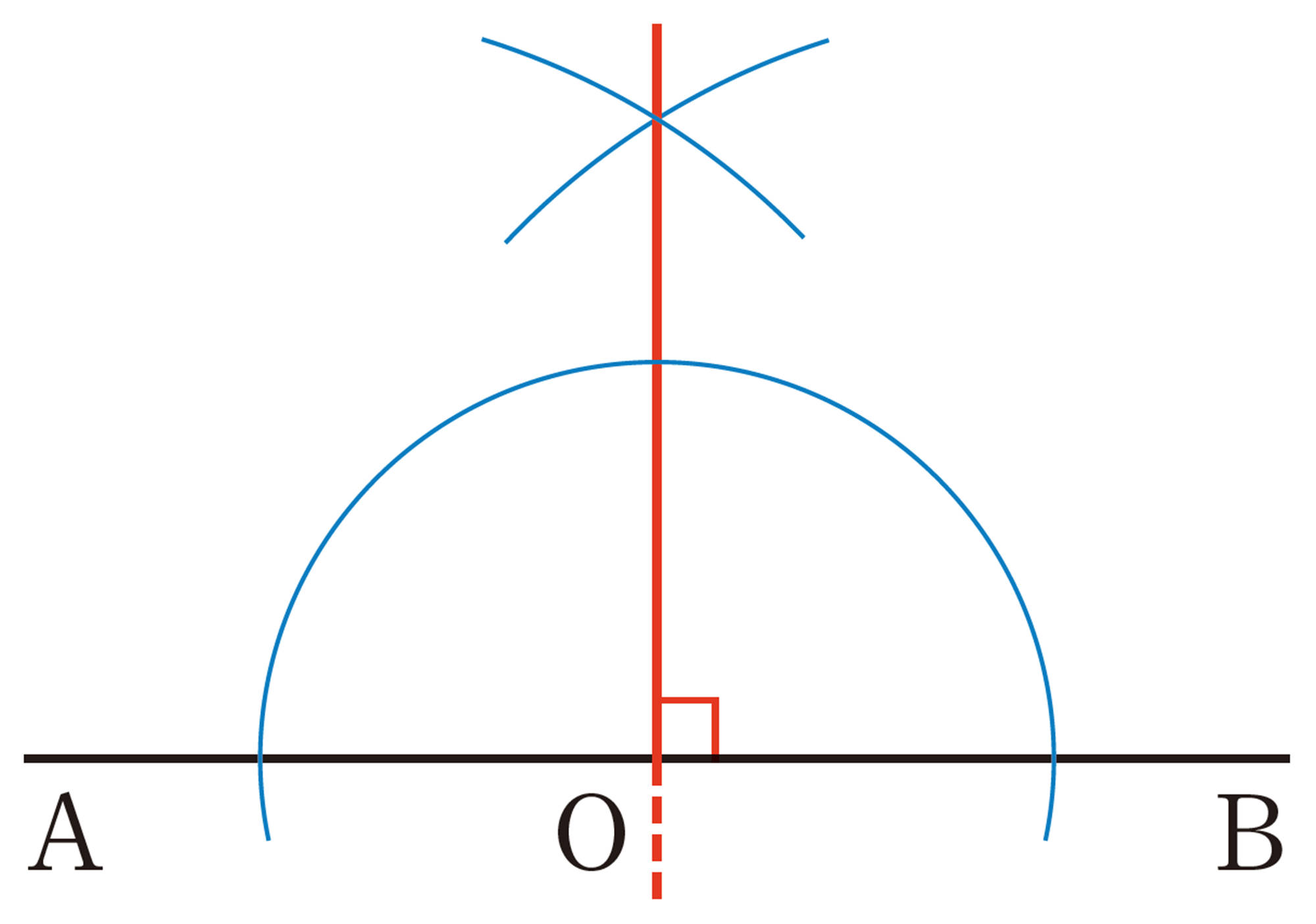
[mathjax]\(90^{\circ}\)の角を作図したときは,ひし形の対角線を利用したね。
見方・考え方
図形の中にある[mathjax]\(60^{\circ}\)の角に着目して考えられるかな。
目標 ▷ [mathjax]\(60^{\circ}\)の角の作図のしかたを考えよう。
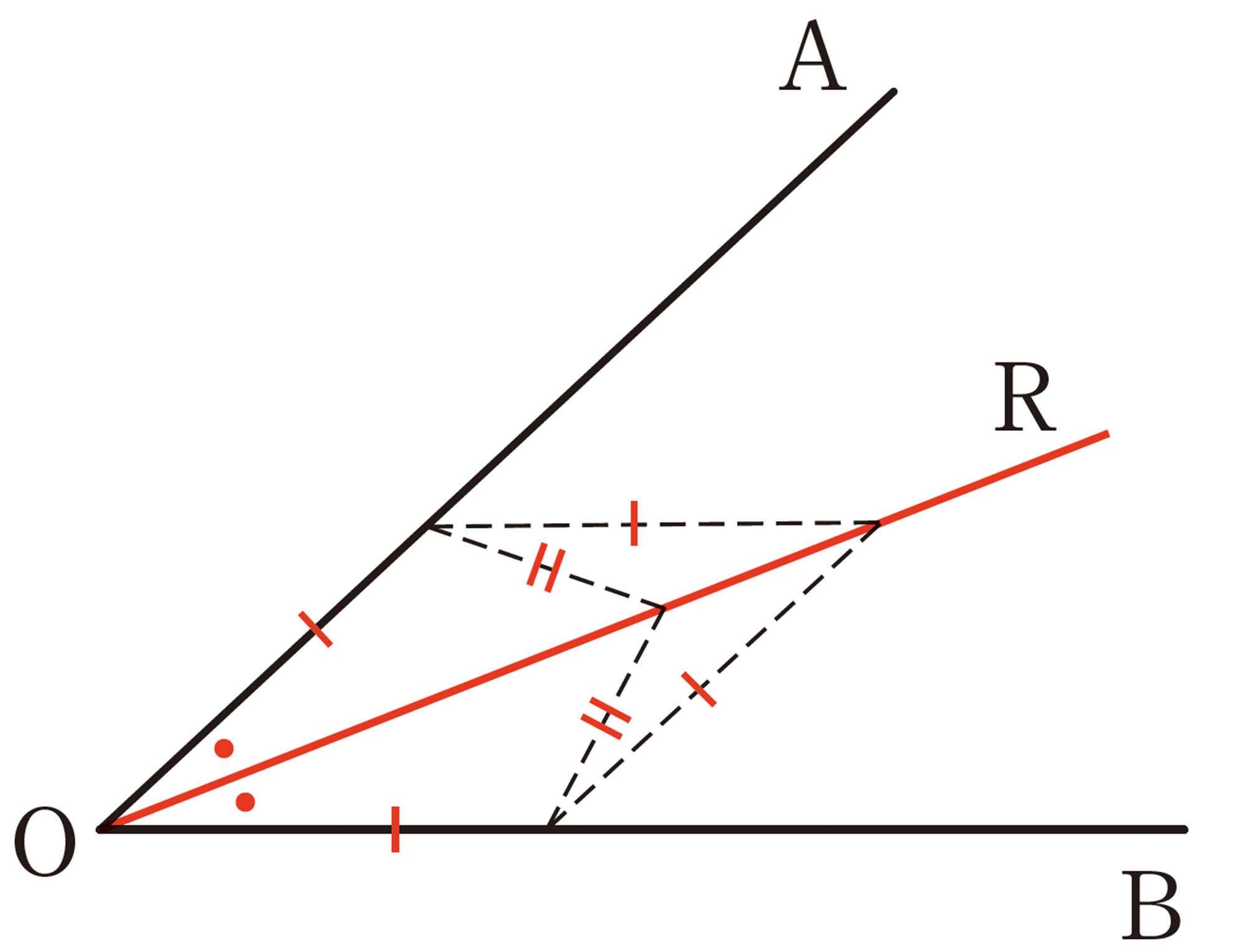
問 1 例1の手順で,[mathjax]\(60^{\circ}\)の角の作図ができる理由を説明しなさい。
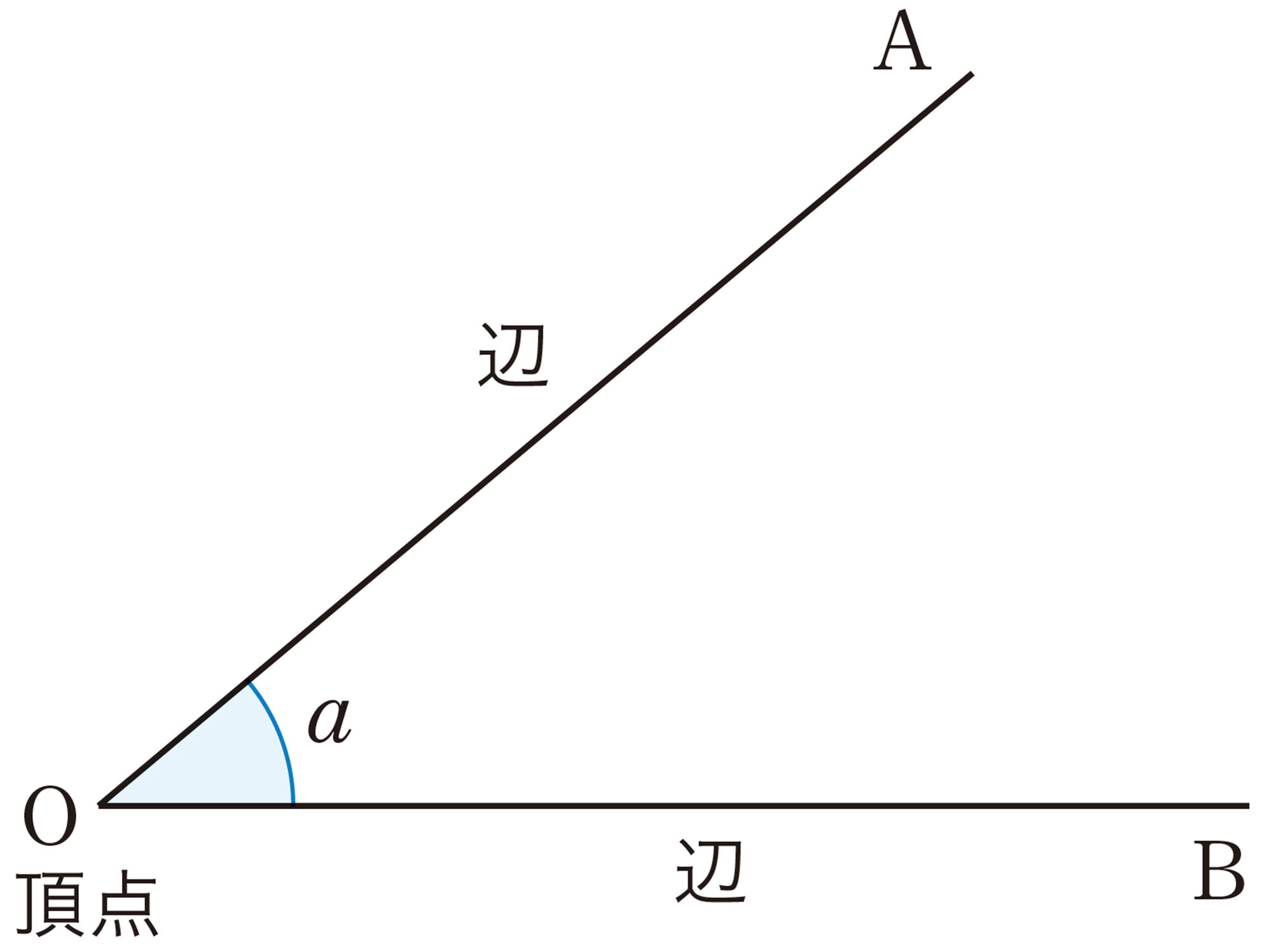
注意 上の図の[mathjax]\(\angle AOB\)は,[mathjax]\(\angle BOA\)と表してもよい。また,単に[mathjax]\(\angle O\)と表したり,角に記号をつけて[mathjax]\(\angle a\) のように表したりすることがある。
<1年p.182>
角の二等分線の作図
Q Question
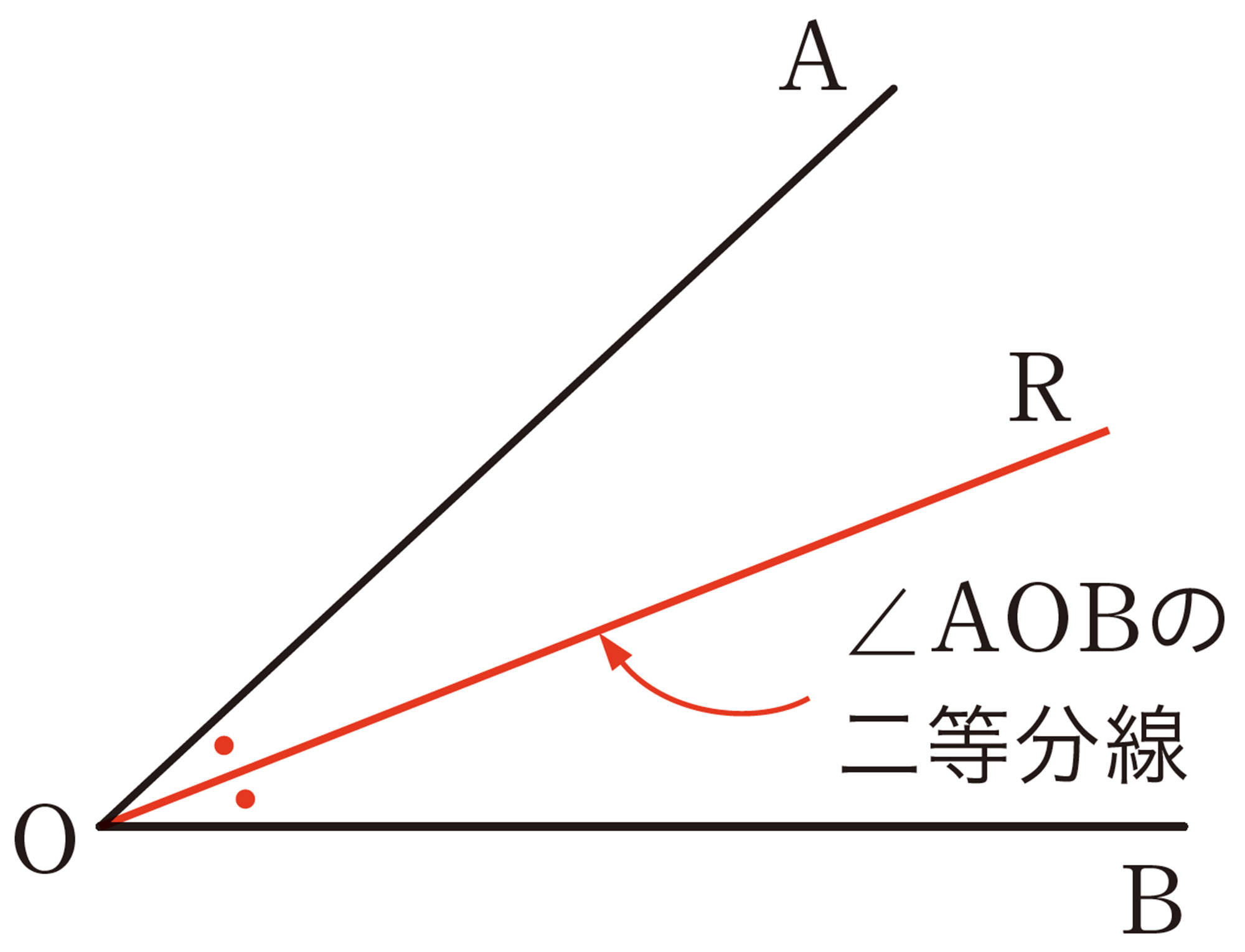
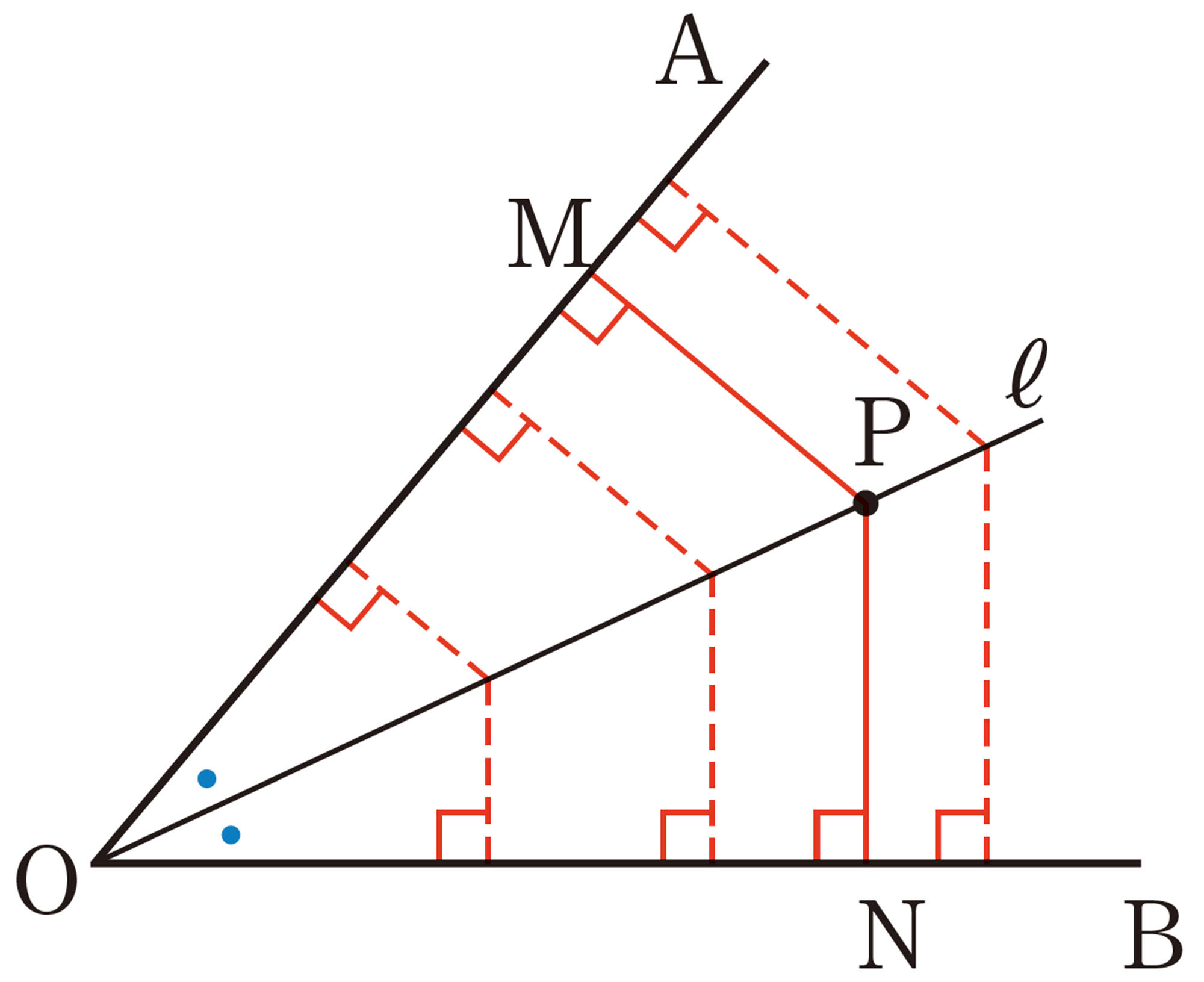
[mathjax]\(30^{\circ}\)の角を作図するには,どのようにすればよいでしょうか。
[mathjax]\(30^{\circ}\)の角の作図に利用できる図形があるか話し合ってみましょう。

[mathjax]\(30^{\circ}\)は[mathjax]\(90^{\circ}\)から[mathjax]\(60^{\circ}\)をひけばいいね。
[mathjax]\(60^{\circ}\)の角を半分にできるかな。

見方・考え方
[mathjax]\(60^{\circ}\)の角をもとにして考えられるかな。
問 3 例2を,たこ形を利用して作図しなさい。
<1年p.183>