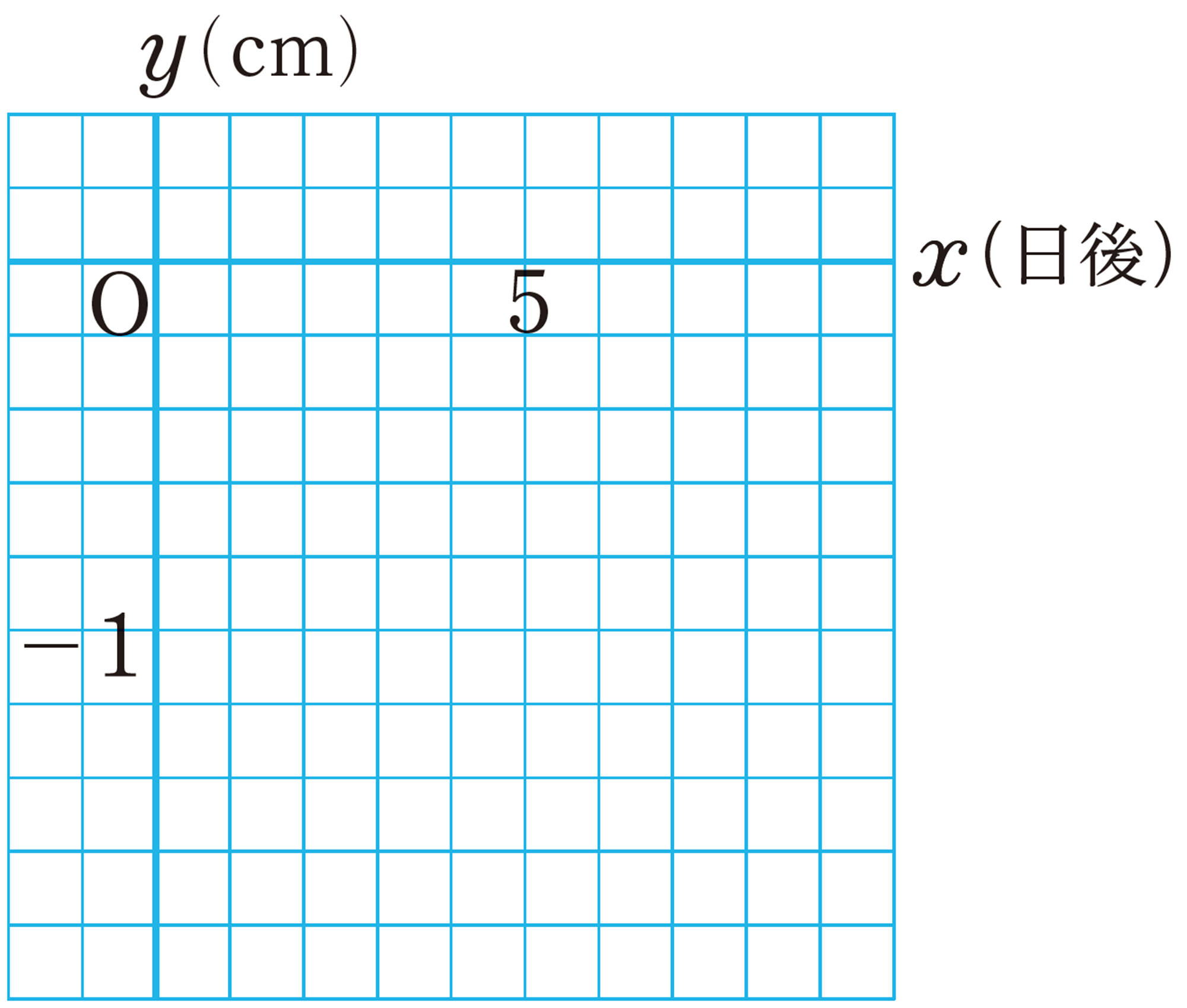<1年p.155>
4節 比例と反比例の利用
どんなところで利用できる？
身のまわりには，比例や反比例の関係にあることがらがたくさんあります。
そのような身のまわりのことがらについて，調べてみましょう。
【１】 比例や反比例の関係にあることがらにはどんなものがあるでしょうか。
速さ，時間，道のりのうちの2つの関係も比例や反比例だったね。
針金の長さと重さの関係は，小学校でも学習したね。
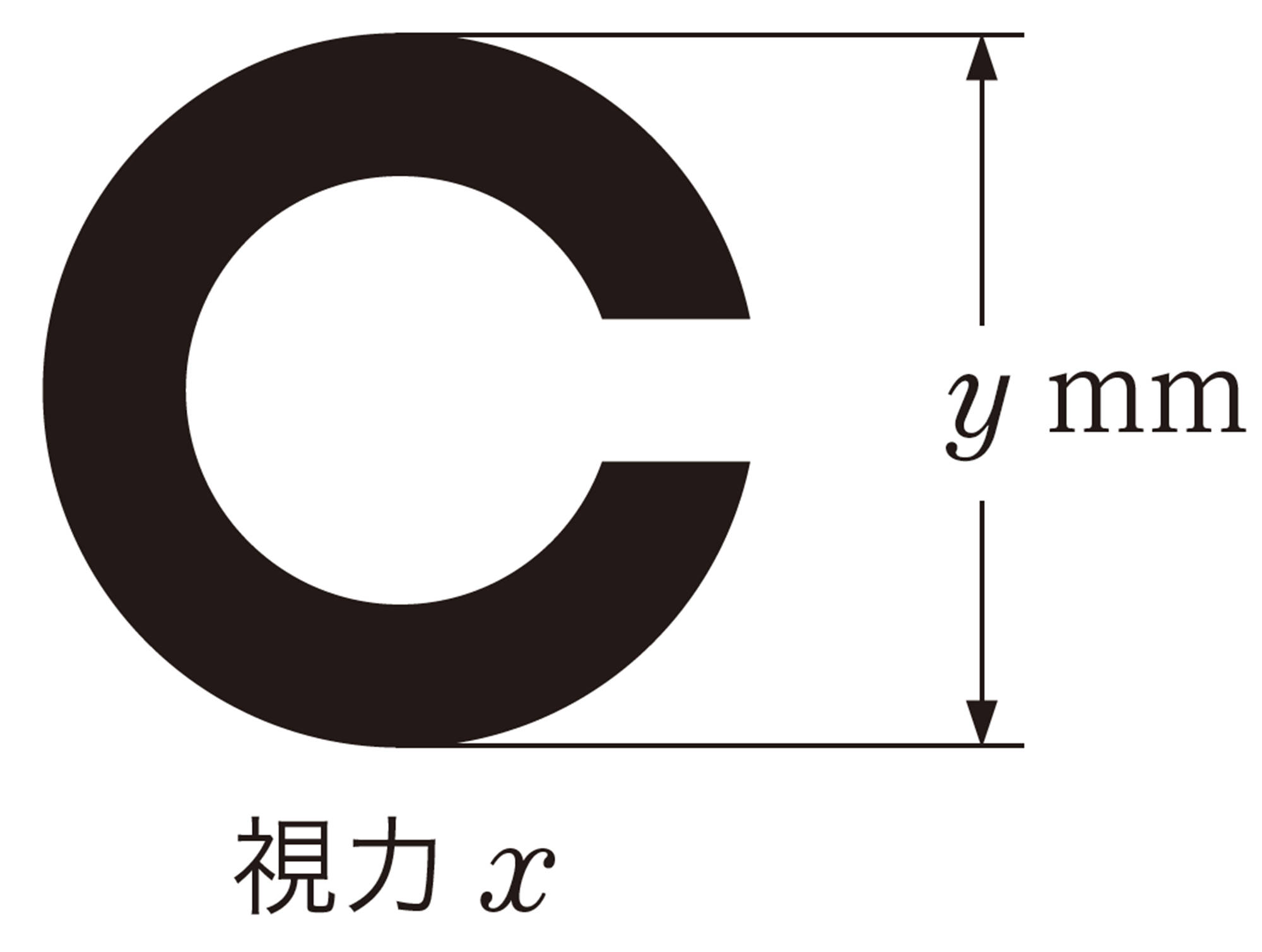
視力検査表は，視力がいいほど図が小さくなるけど，比例や反比例の関係にあるのかな。
次の課題へ！
比例や反比例の関係は，身のまわりでどのように利用されているのかな？
P.155
１ 比例と反比例の利用
目標 ▷ 比例や反比例の関係を利用して，身のまわりの問題を解決しよう。
Q Question
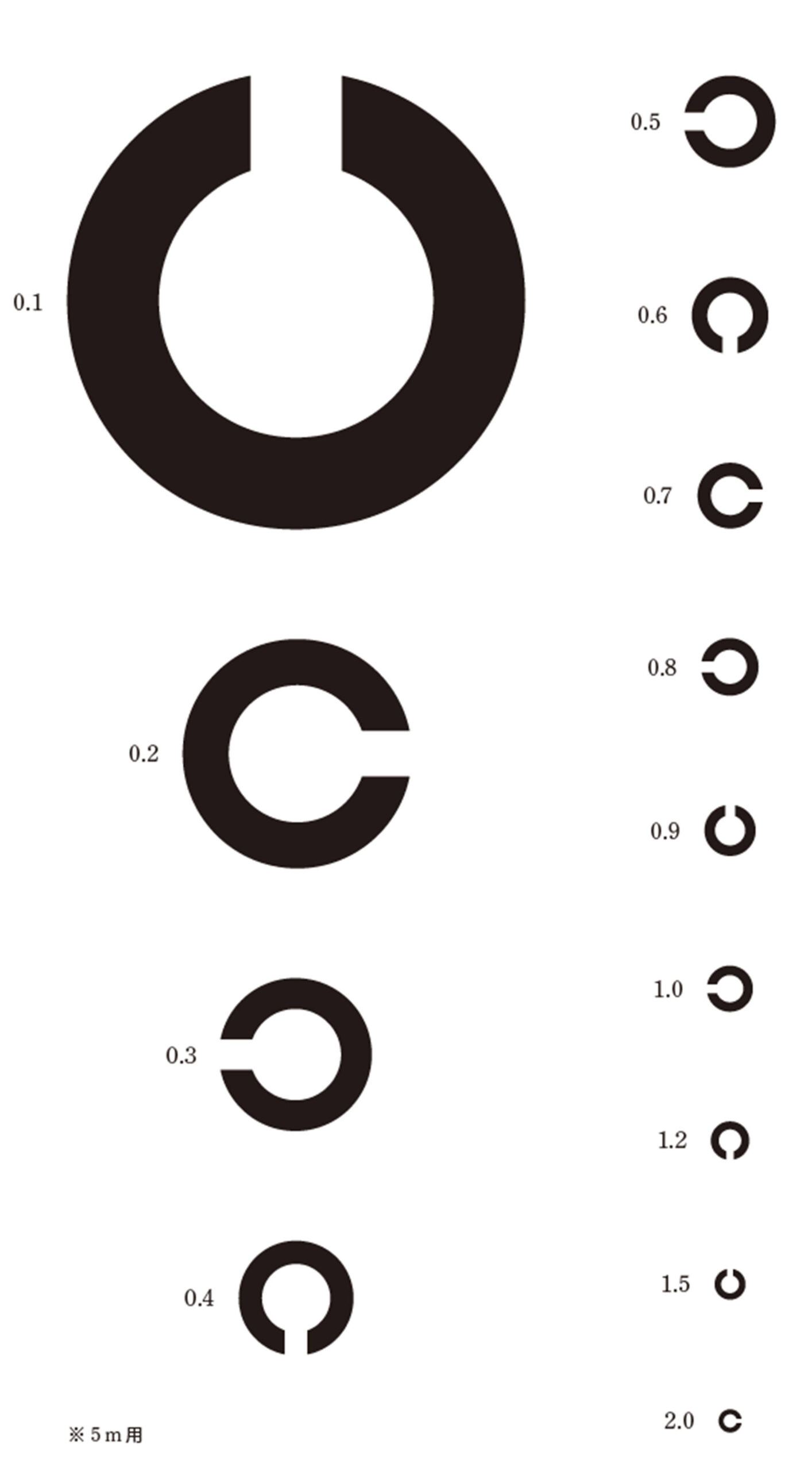
学校の健康診断などで行われる視力検査では，157ページの図のような，ランドルト環と呼ばれる，一部分にすき間があいている図を使った，視力検査表が用いられています。この視力検査表で，ともなって変わる2つの数量を探し，その数量がどんな関係になっているか調べてみましょう。
視力の値が大きくなると，ランドルト環は小さくなるね。
実際にランドルト環の大きさを測れば，視力とランドルト環の大きさの関係がわかるかな。
見方・考え方
対応する2つの数量関係に着目して考えられるかな。
<1年p.156>
１ 視力をx，環の外側の直径をy mm として，xとyの関係を調べます。次ページの視力検査表を使って外側の直径を測り，次の表に書き入れましょう。
注意 定規などで測定する場合，正確に測れないことがあるが，測定して得られた値を真の値とみなして考える。
２ 上の表から，視力xと外側の直径y mm の間には，どんな関係があるでしょうか。左の図にグラフをかき入れて考えましょう。
また，xとyの関係を式に表しましょう。
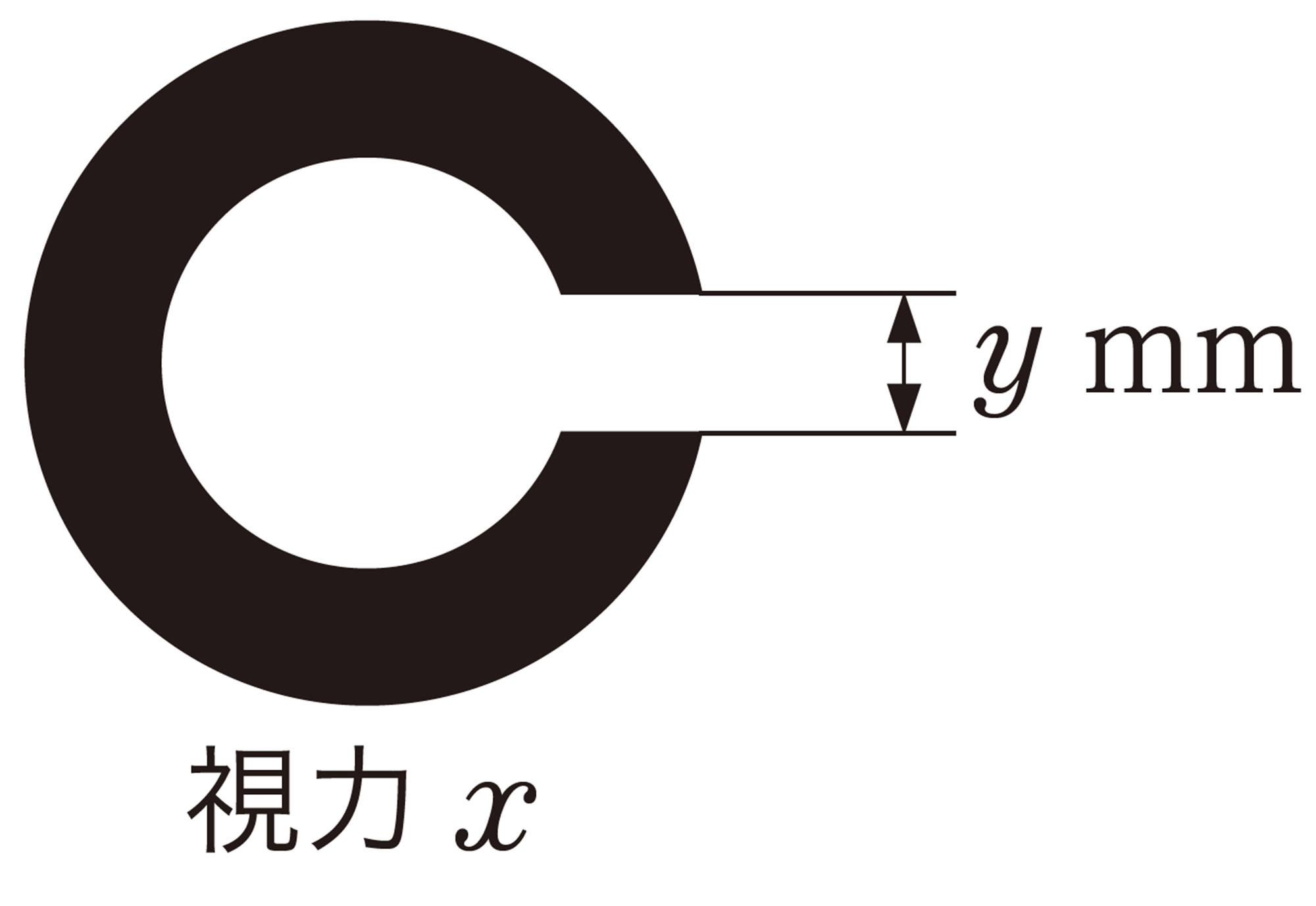
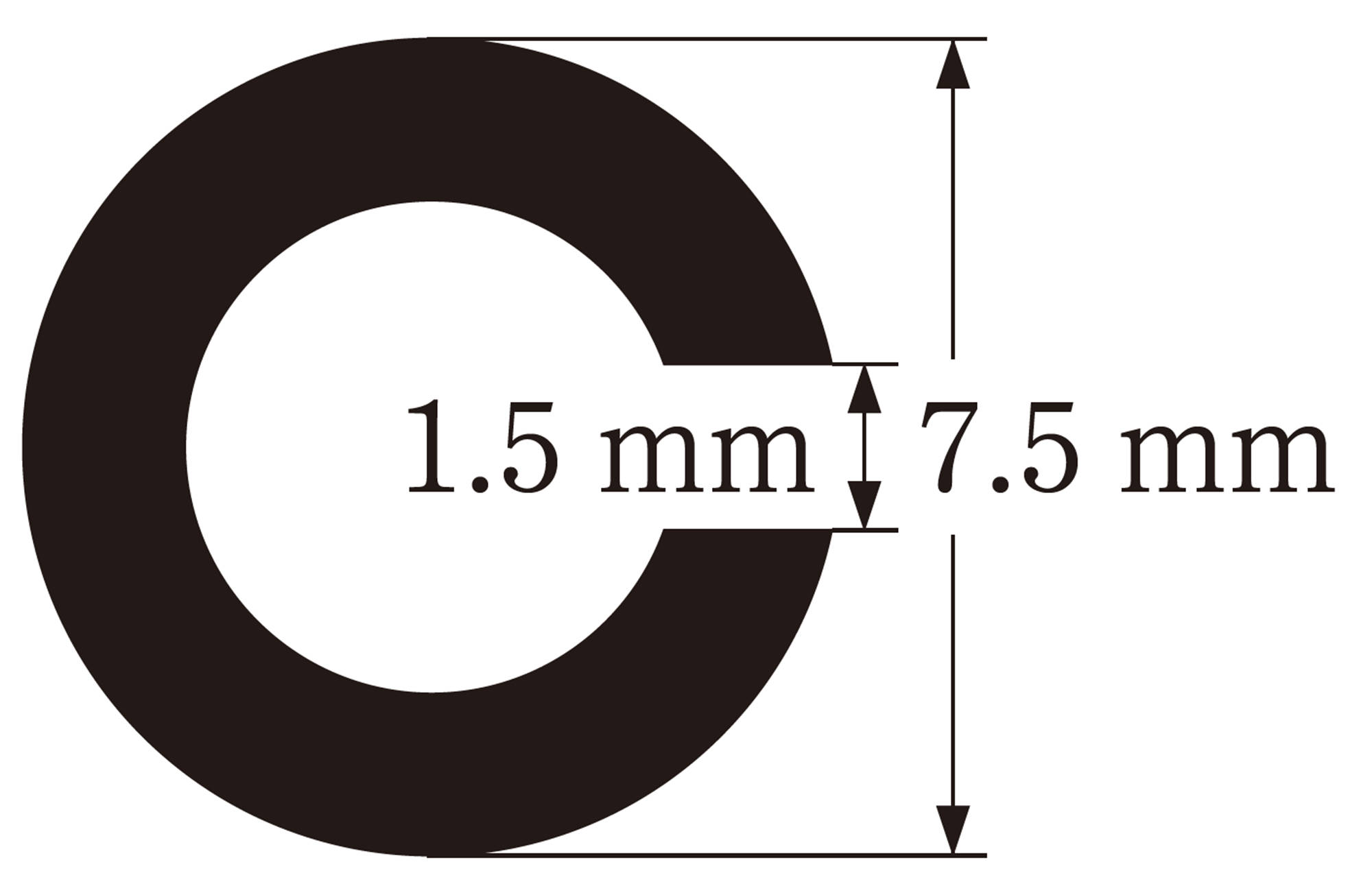
４ 視力[mathjax]\(0.05\)を測るためのランドルト環の外側の直径とすき間の幅を求めてみましょう。
ランドルト環は，1909年の国際眼科学会で，国際的な標準指標として採用されました。このとき，「視力をどのように数値化するか」が話し合われ，「直径[mathjax]\(7.5\) mm，すき間の幅[mathjax]\(1.5\) mm の大きさのランドルト環を，5 m 離れたところから見て，すき間のあいた方向を判別できた視力を[mathjax]\(1.0\)とする」と定められました。
<1年p.157>
<1年p.158>
アフリカのマサイ族の視力は[mathjax]\(8.0\)と聞いたことがあるけど，ランドルト環で測れるのかな。
ランドルト環までの距離を変えたらどうかな。
５ 外側の直径が[mathjax]\(7.5\) mmのランドルト環1つで視力を調べたいと思います。物を見るとき，距離を2倍，3倍，…にすると，物の大きさは [mathjax]\(\dfrac{1}{2}\)倍，[mathjax]\(\dfrac{1}{3}\)倍，…に見えるとするとき，次の問いを考えてみましょう。
⑴ 視力[mathjax]\(8.0\)であるかどうかを調べるには，何 m 離れたところから調べればよいでしょうか。また，視力[mathjax]\(0.5\)のときはどうでしょうか。
⑵ 視力xを調べるために離れる距離をym とすると，xとyはどんな関係にあるといえるか説明してみましょう。
問 １ 美月さんの家の玄関に，右のような手指消毒用アルコールを置くことになりました。美月さんは， アルコールがなくなったらすぐに新しいものに取り替えたいと考えました。置く前のアルコールの入っている高さが14 cmのとき，何日後になくなるかを予想する方法を話し合いなさい。
どうやって考えればいいかな。
初めの高さを0として，1日でどのくらい減るか調べてみたらどうかな。
1日後，アルコールは初めより[mathjax]\(0.2\) cm減っていました。
1日で[mathjax]\(0.2\) cmずつ減る比例と考えよう。
え，本当に比例なの。1組の値だけで判断していいのかな。
データを増やして，グラフに表してみればいいよ。
グラフが原点を通る直線になっていれば比例だとわかるね。
置く前のアルコールが入っていた高さを0 cm とし，x日後のアルコールの高さをy cm として5日後までのデータを取ると，次の表のようになりました。
<1年p.159>
⑴ xとyの関係は，どのようなグラフになりますか。表の対応するxとyの値の組を右の図にかき入れて話し合いなさい。
点は一直線上に並ばないね。
でも，ほぼ一直線上に並んでいると考えてもいいと思う。
原点と点[mathjax] \((2，-0.6)\)を通る直線を引くと，点[mathjax] \((3，-0.9)\)と[mathjax] \((5，-1.5)\)も通るね。
⑵ アルコールが何日後になくなるかの求め方を話し合いなさい。
この表やグラフだと，5日後より先がわからないね。
式で考えればいいと思う。
式がわかれば，何日後になくなるかを求めることができそうだね。
比例の式 [mathjax]\(y=ax\)のaを求めるには何がわかればいいかな。
⑶ 美月さんは，アルコールが何日後になくなるかを，次のように求めようとしています。続きを説明しましょう。
アルコールの高さは日数に比例するとみなして，x日後のアルコールの高さをy cm とすると，[mathjax]\(y=ax\)と表すことができる。
aを求めるには1組のx，yがわかればよいので，グラフが通る点の１つ[mathjax]\(x=2\)，[mathjax]\(y=-0.6\) を[mathjax]\(y=ax\)に代入すると，[mathjax]\(-0.6=a \times 2\)
⑷ アルコールは，何日後になくなると考えられますか。
問１のように，xとyの関係を表すグラフが原点を通る直線とみなすことができると，その関係は比例であると考えることができる。比例と考えることができれば，式に表すことができ，問題が解きやすくなる。
また，グラフをかくときには，できるだけ多くの点を通るか，点の近くを通るようにする。
<1年p.160>
例 １ 大和さんは，コンビニエンスストアで弁当を買いました。そのラベルに，右のような電子レンジでの加熱時間が表示されていました。電子レンジの出力と加熱時間の間には，反比例の関係があります。次の問いに答えなさい。
⑴ 電子レンジの出力をxW，加熱時間をy秒としたとき，yをxの式で表しなさい。
⑵ 電子レンジの出力が600Wのとき，この弁当の加熱時間を求めなさい。
解答
⑴ [mathjax] \(xy\) の値が一定の45000 になるので， 式は次のようになる。
[mathjax] \(y =\dfrac{45000}{x}\)
答 [mathjax] \(y = \dfrac{45000}{x} \)
⑵ ⑴で求めた式に，[mathjax] \(x=600\) を代入すると，
答 75 秒
例 ２ 右下の図のように，歯車A，Bがかみ合って，それぞれ回転しています。
Aの歯の数は30で，1秒間に6回転します。Bには，いろいろな歯車を取りつけることができます。次の問いに答えなさい。
⑴ Bの歯の数が60のとき，Bは1秒間に何回転しますか。
⑵ Bの歯の数をx，Bの1秒間の回転数をyとして，yをxの式で表しなさい。
解答
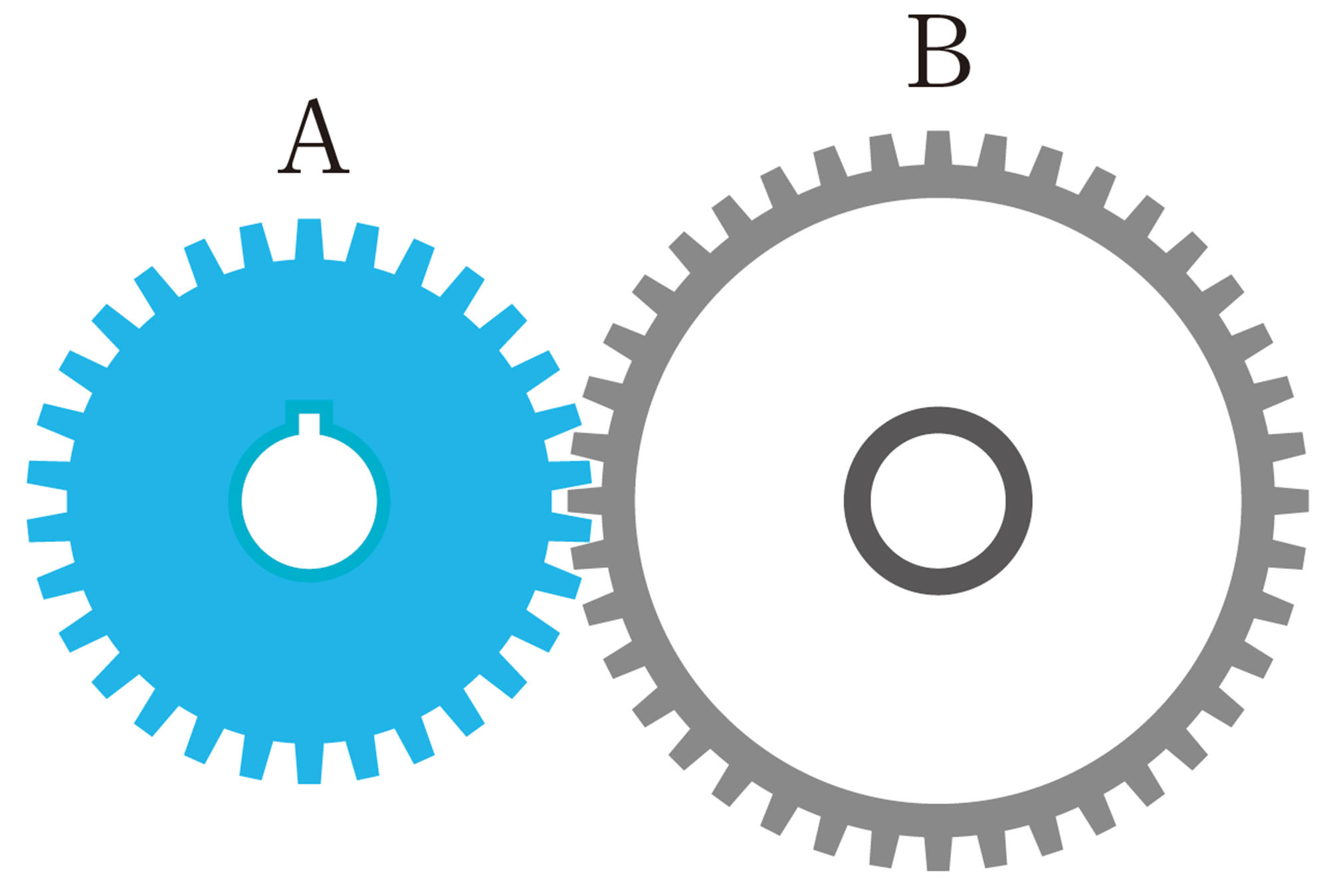
⑴ 歯車A とB は同じ歯の数だけかみ合う。歯車A とB の歯は1秒間では，
[mathjax]\(30\times 6=180\)
より， 180 個分ともに進む。したがって， 歯車B の1 秒間の回転数は，
[mathjax]\(180\div 60=3\)
より， 3 回転する。
答 3 回転
⑵ 歯車B の歯は1 秒間に180 個分進むので， [mathjax] \(xy=180\) より，
[mathjax]\(y=\dfrac{180}{x}\)
答 [mathjax] \(y=\dfrac{180}{x}\)
<1年p.161>
問 ２ 右下の図のような天びんがあります。支点より左には乾電池をつるして固定し，支点より右にはおもりをつるし，おもりの重さと支点からの距離をいろいろ変えて，左右がつり合うようにします。
このとき，おもりの重さx g と支点からの距離y cm の関係を調べたところ，次の表のようになりました。下の問いに答えなさい。
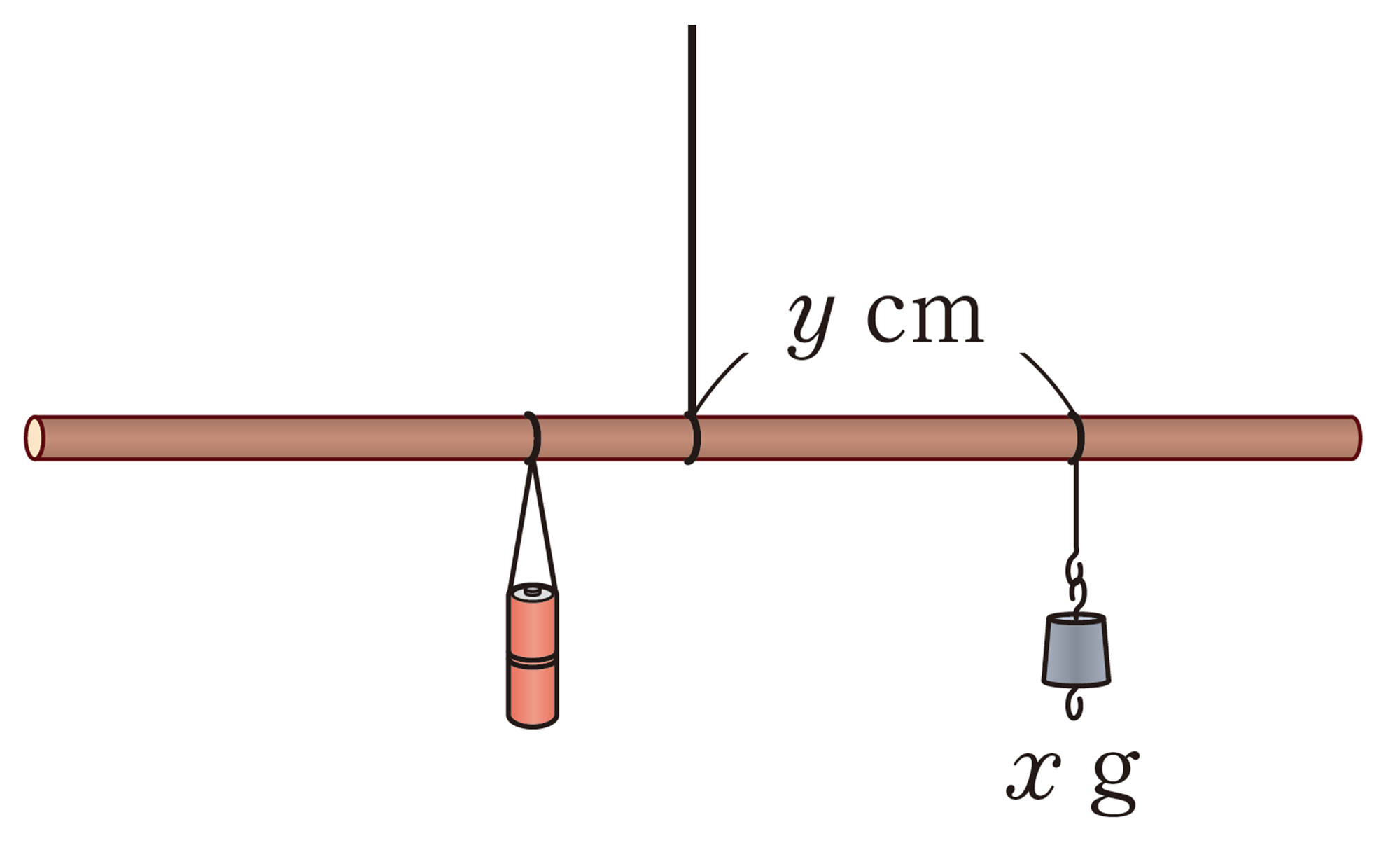
⑴ yをxの式で表しなさい。
⑵ xとyはどんな関係にありますか。
⑶ 60 gのおもりをつるすとき，支点から何 cm の距離でつり合いますか。
⑷ 支点から12 cmの距離でつり合うのは何 g のおもりですか。
竿ばかり Tea Break
右の写真は，「竿ばかり」と呼ばれる，物の重さを量る道具です。支点につけたひもで竿をつるし，竿の先端に物をつり下げ，支点の反対側ではおもりを動かしてつり合わせ，おもりの位置の目盛りを読んで物の重さを量ります。
竿ばかりは，紀元前200年頃，古代ローマで発明されたといわれています。日本へは中国から伝わり，明治時代に入るまで広く使われていました。竿ばかりには，重さを長さにおきかえて量る，支点からの距離を変えて軽いおもりで重い物も量れるようにする，などの知恵が込められています。
