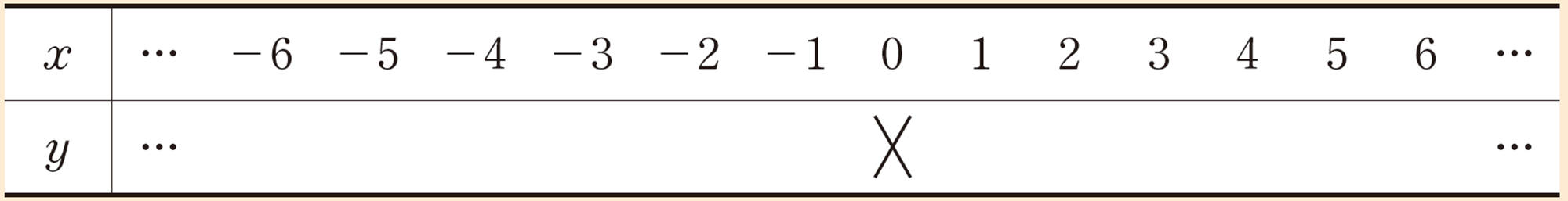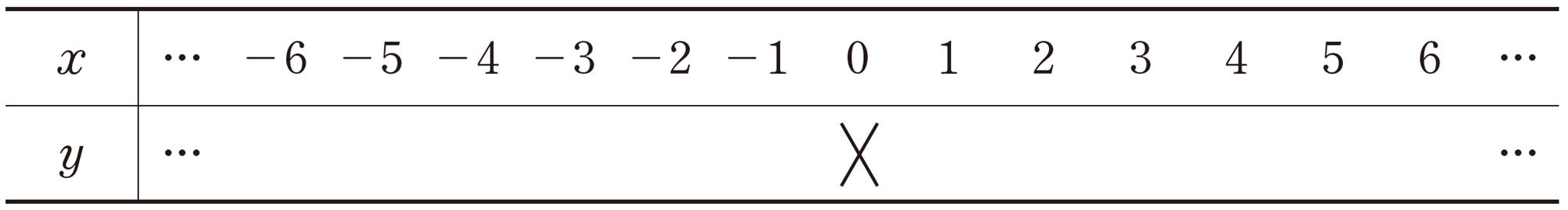<1年p.147>
3節 反比例
変域を負の数まで広げたらどうなる？
変域や比例定数が負の数になる比例について考えました。
反比例についても，負の数をふくめて考えられるか調べてみましょう。
反比例も小学校で学習したけど，正の数だけだったね。
反比例も，比例と同じように，数の範囲を負の数まで広げて考えられるかな。
小学校では，yがxに反比例するとき，その関係を式に表すと，
[mathjax]\(xy=\)決まった数
になったね。
たとえば，反比例の式[mathjax]\(xy=6\)について，数の範囲を負の数まで広げて調べてみよう。
【１】 [mathjax]\(xy=6\)について，xの変域を負の数まで広げたときのxとyの関係を，次の表にまとめ，気づいたことを話し合いましょう。
注意 上の表の☓印は，[mathjax]\(x=0\)を除いて考えることを示している。
比例では，変域が負の数でも比例といえたね。
反比例でも，比例と同じように考えてみよう。
次の課題へ！
変域を負の数まで広げても，反比例といえるのかな？
P.148
<1年p.148>
１ 反比例と式
Q Question
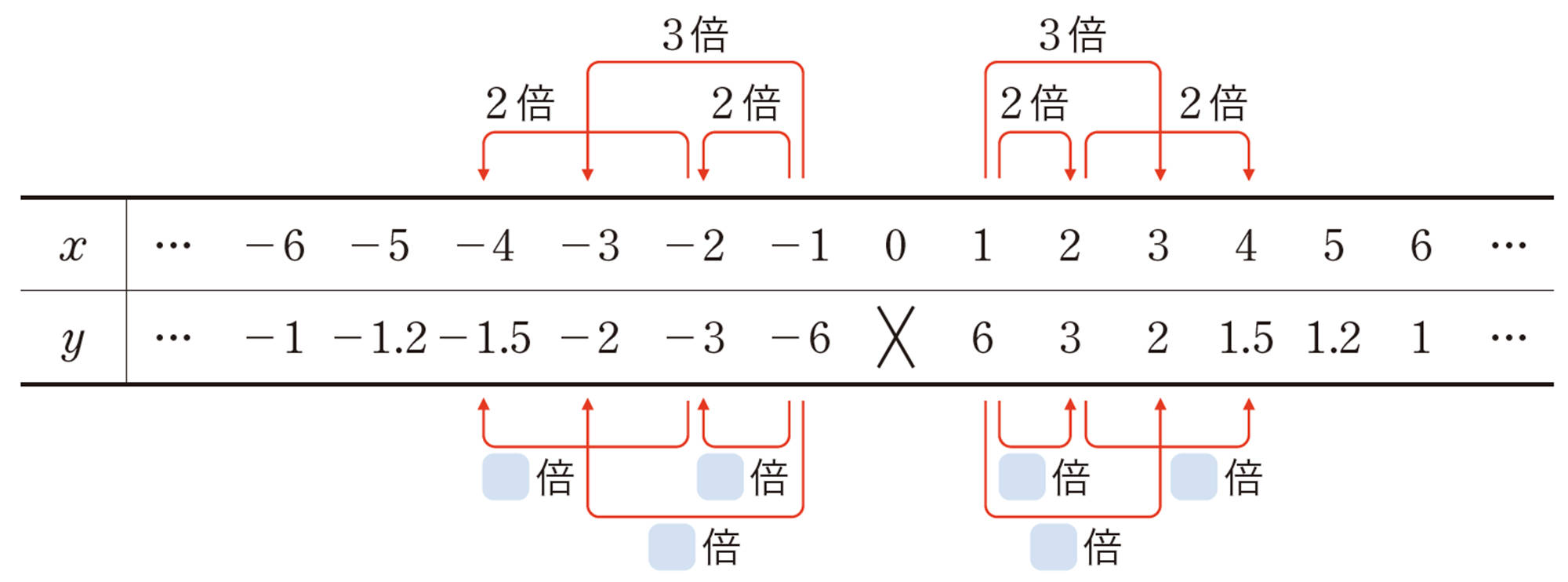
前ページの【1】について，xの値が2倍，3倍，…になると，yの値はどうなるでしょうか。
[mathjax]\(x\gt 0\)，[mathjax]\(x \lt 0\)のそれぞれの変域で調べてみましょう。
変域を負の数まで広げても反比例といえるのかな。
見方・考え方
どんな関係なら，反比例しているといえるのかな。
目標 ▷ 変域や比例定数を負の数まで広げたときの反比例について考えよう。
xとyの関係を表した式[mathjax]\(xy=6\)を，yをxの式で表すと，[mathjax]\(y=\dfrac{6}{x}\)になる。
反比例
yがxの関数であり，次のような式で表されるとき，yはxに反比例する という。
[mathjax]\(y=\dfrac{a}{x}\)
ただし，aは0でない定数で，このaを 比例定数 という。
yがxに反比例するとき，積xyの値は一定で，この値が比例定数aである。
<1年p.149>
例 １ 12 kmの道のりを時速x kmで歩くときにかかる時間をy時間とするとき，yをxの式で表すと，[mathjax]\(y=\dfrac{12}{x}\)となる。したがって，yはxに反比例し，比例定数は12である。
問 １ 次の⑴ ～ ⑶について，yをxの式で表しなさい。また，yはxに反比例するといえますか。反比例しているものについては，比例定数をいいなさい。
⑴ 18 m のロープをx等分したとき，1本分の長さがy m である。
⑵ 500 mLのジュースをx mL 飲んだとき，残りがy mLである。
⑶ 面積30 cm² ，底辺x cm の三角形の高さがy cm である。
問 ２ 関数[mathjax]\(y=-\dfrac{6}{x}\)について，次の問いに答えなさい。
⑴ yはxに反比例するといえますか。また，その理由を説明しなさい。
⑵ xとyの関係を，次の表にまとめなさい。
⑶ xの値が2倍，3倍，…になると，yの値はどうなりますか。[mathjax]\(x \gt 0\)，[mathjax]\(x \lt 0\)のそれぞれの変域で調べなさい。
反比例でも比例定数が負の数になる場合がある。
関数[mathjax]\(y=-\dfrac{6}{x}\)は，比例定数が-6のときの反比例の関係を表している。
問 ３ 次の式で表すことができる関数のうち，yがxに反比例するものはどれですか。また，そのときの比例定数をいいなさい。
㋐ [mathjax]\(y=\dfrac{12}{x}\)
㋑ [mathjax]\(y=\dfrac{x}{12}\)
㋒ [mathjax]\(y=-\dfrac{4}{x}\)
㋓ [mathjax]\(xy=-20\)
<1年p.150>
反比例の式の求め方
例 ２ yはxに反比例し，[mathjax]\(x=12\)のとき[mathjax]\(y=6\)です。yをxの式で表しなさい。また，[mathjax]\(x=9\)のときのyの値を求めなさい。
解答
[mathjax]\(y\) は[mathjax]\(x\)に反比例するから， 比例定数を[mathjax]\(a\) とすると，
[mathjax] \(\hspace{ 60pt }y= \dfrac{a}{x} \)
[mathjax] \(x=12\) のとき[mathjax] \(y=6\)であるから， これらを代入すると，
[mathjax]\(\hspace{ 60pt } 6 =\dfrac{a}{12} \)
これを解くと，[mathjax] \(a=72\)
したがって，[mathjax]\(\hspace{ 12pt } y=\dfrac{72}{x}\)
この式に[mathjax] \(x=9\) を代入すると，
[mathjax]\(\hspace{ 60pt } y=\dfrac{72}{9}\)
[mathjax]\(\hspace{ 68pt }=8 \)
答 [mathjax] \(y = \dfrac{72}{x}\)，[mathjax] \(y=8\)
問 ４ yがxに反比例するとき，次の ⑴，⑵ のそれぞれの場合について，yをxの式で表しなさい。また，[mathjax] \(x=-3\)のときのyの値を求めなさい。
⑴ [mathjax]\(x=2\)のとき[mathjax]\(y=9\)
⑵ [mathjax]\(x=6\)のとき[mathjax]\(y=-4\)
問 ５ 1分間に4L ずつ水を入れると，1時間で満水になる浴そうがあります。次の問いに答えなさい。
⑴ この浴そうには，何 L の水が入りますか。
⑵ 1分間にxLずつ水を入れると，y分で満水になるとするとき，yをxの式で表しなさい。
⑶ 1分間に5L ずつ水を入れると，何分で満水になりますか。
どんなことがわかったかな
反比例でも，比例と同じように，変域や比例定数を負の数まで広げて考えることができます。
次の課題へ！
反比例のグラフは，どんな形になるのかな？
P.151
