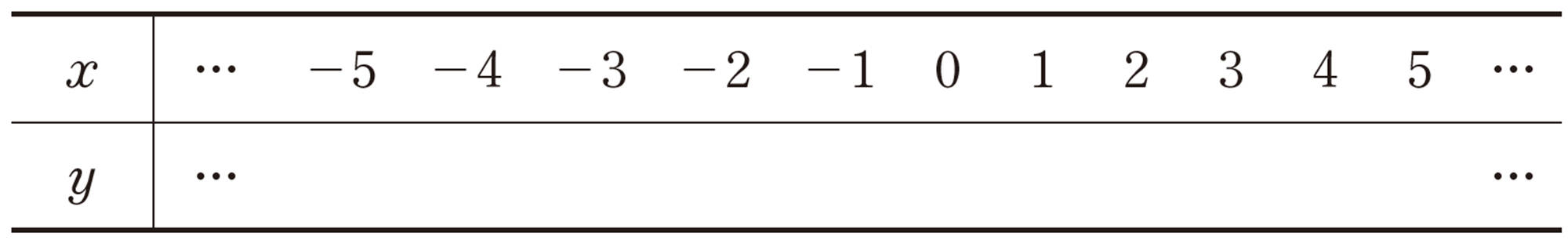<1年p.140>
２ 座標と比例のグラフ
座標
Q Question
右の図に，[mathjax] \(x=-2\)， [mathjax] \(y=-6\)の点を表すには，どうすればよいか考えてみましょう。
xもyも負の数だから，表せる場所がないよ。
数直線は，正の数と反対の方向にのばしたけど，右の図ものばせばいいのかな。
見方・考え方
負の数を表す数直線のときと同じように考えられるかな。
平面上の点の位置は，2つの数の組を使って表すことができる。
たとえば，右の地図の点Aの位置は，「北緯15度，東経30度」と表すことができる。
数の範囲を負の数まで広げたときの点の位置を決めるには，次のように考えればよい。
まず，右の図のように，平面上に直角に交わる2本の数直線を考える。
このとき，横の数直線を x軸，または横軸，縦の数直線を y軸，または縦軸，x軸とy軸を合わせて 座標軸，座標軸の交わる点O を 原点という。また，x軸は，右の方向を正の方向，y軸は，上の方向を正の方向とする。
<1年p.141>
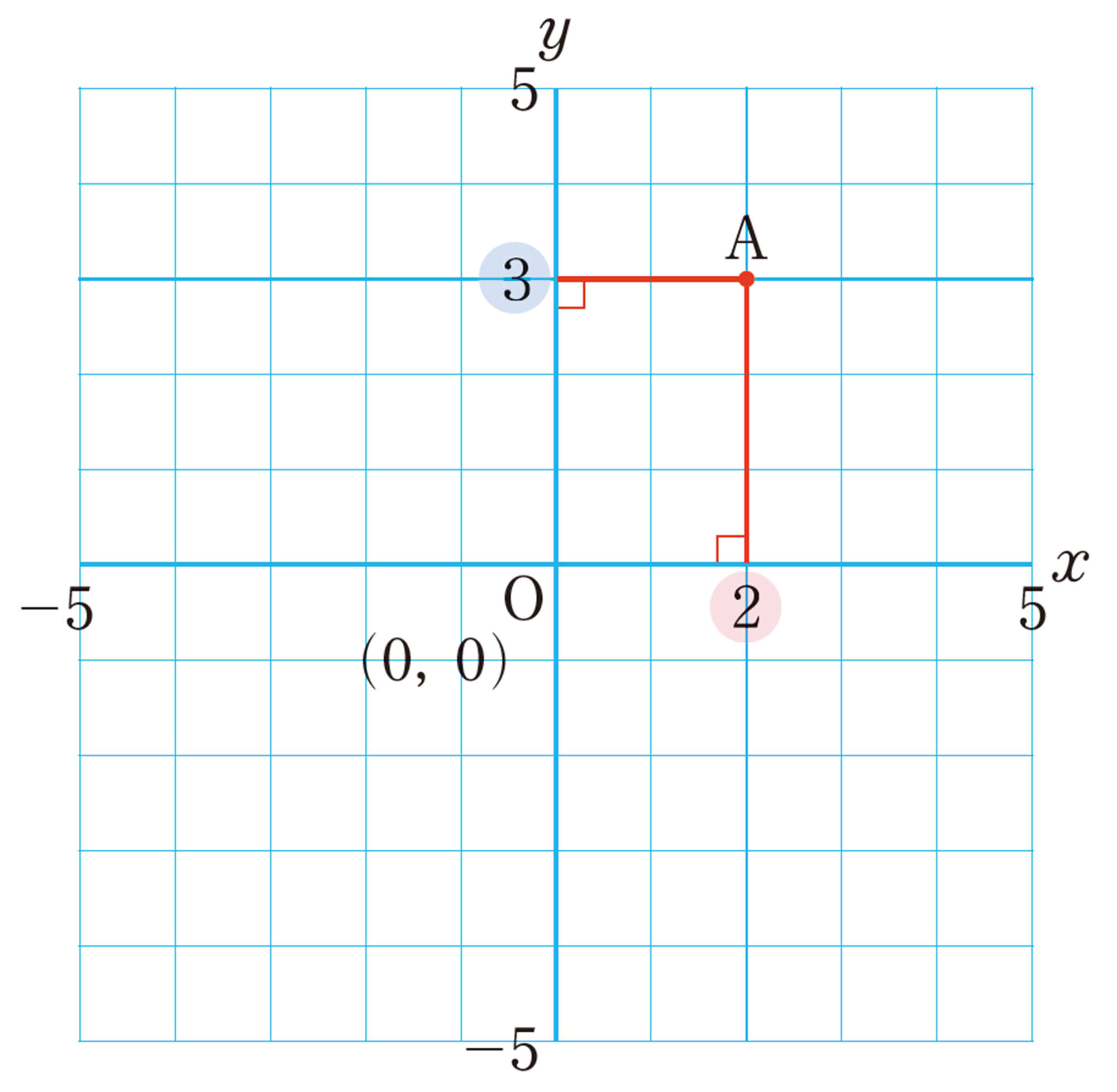
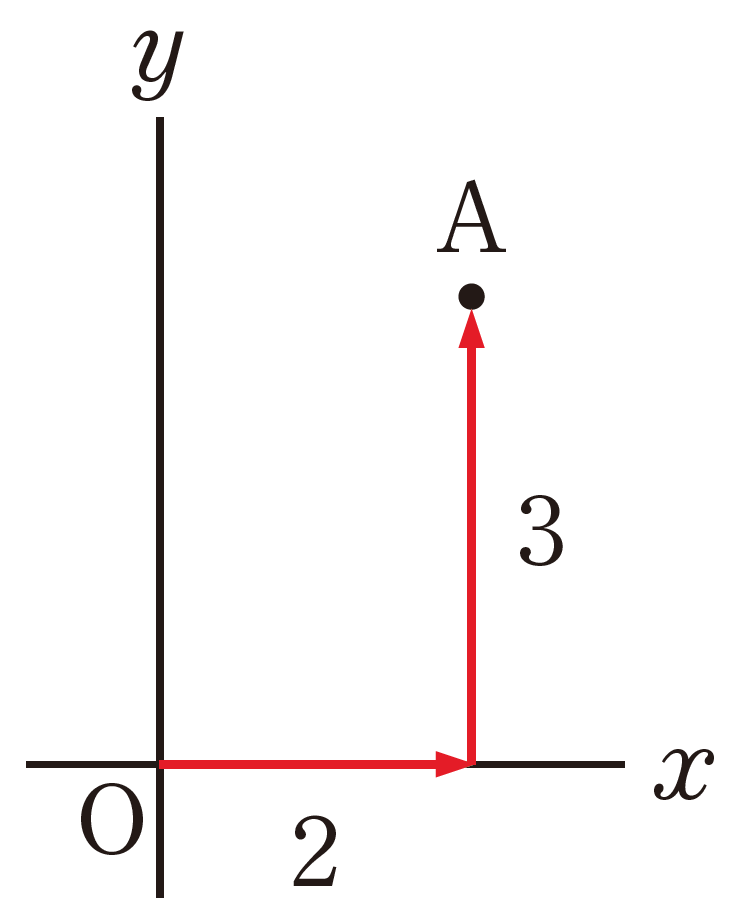
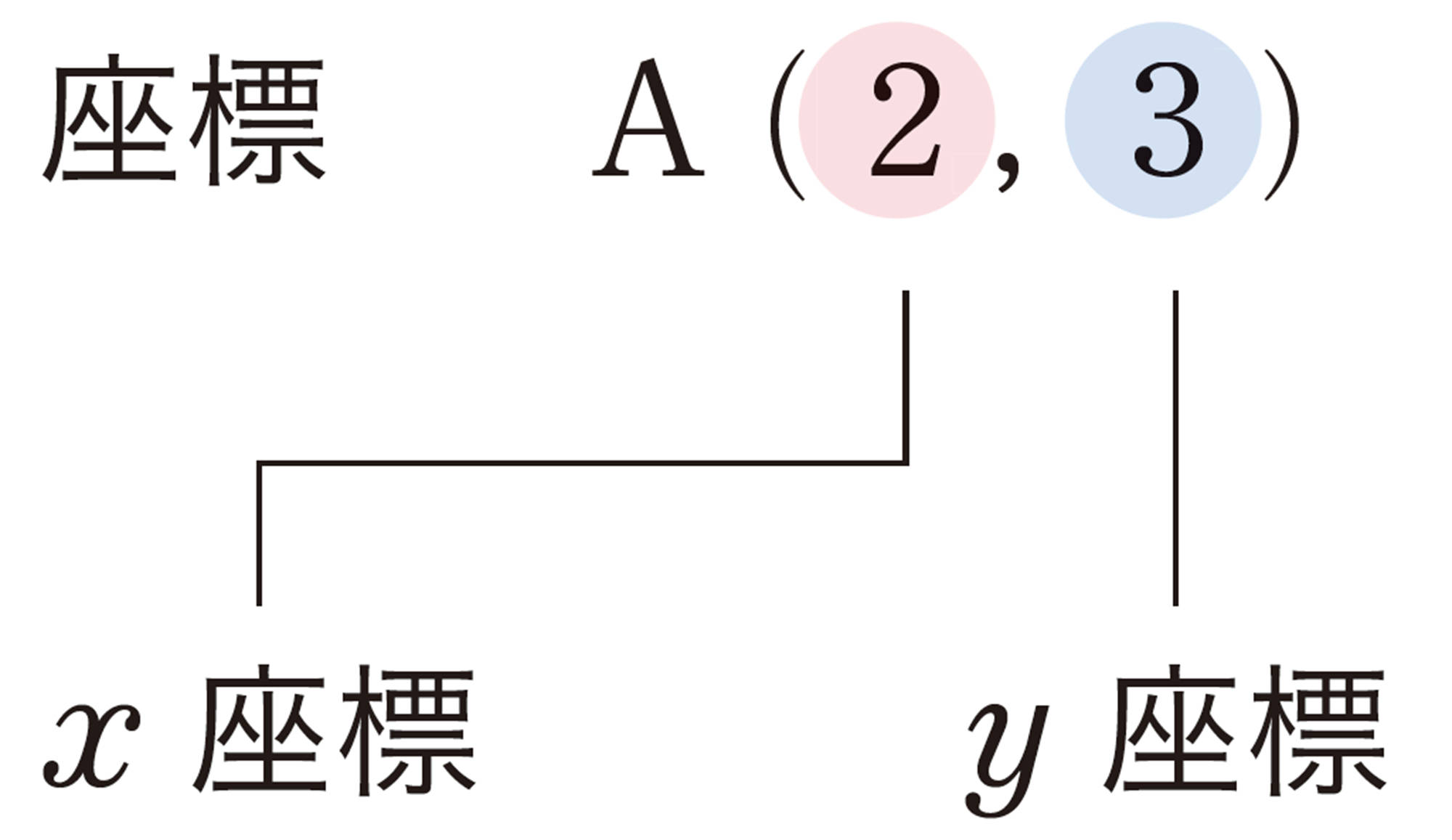
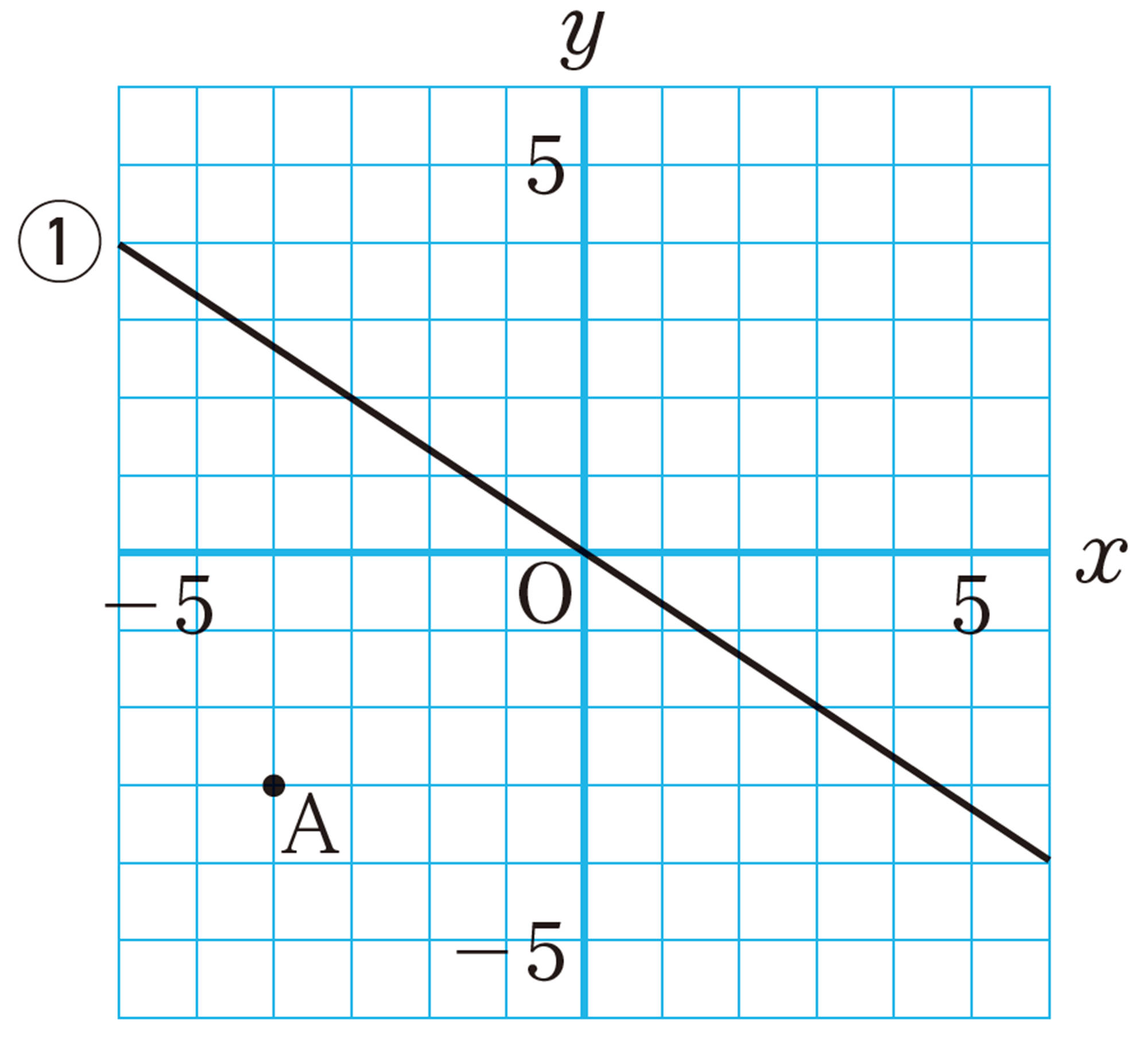
次の図で，点 Aの位置の表し方を考えよう。
点 Aは，原点から右へ2，上へ3進んだ点と考えることもできるね。
点 A からx軸，y軸にそれぞれ垂直な直線を引き，x軸，y軸と交わる点の目盛りの数値を読み取り，点 A を数の組[mathjax]\((2，3)\)で表す。このとき，
2を点 A の x座標 ，
3を点 A のy座標 ，
[mathjax]\((2，3)\)を点 A の 座標
という。
また，点 A を[mathjax]\(A(2，3)\)と表すこともある。
原点 O の座標は，[mathjax]\((0，0)\)である。
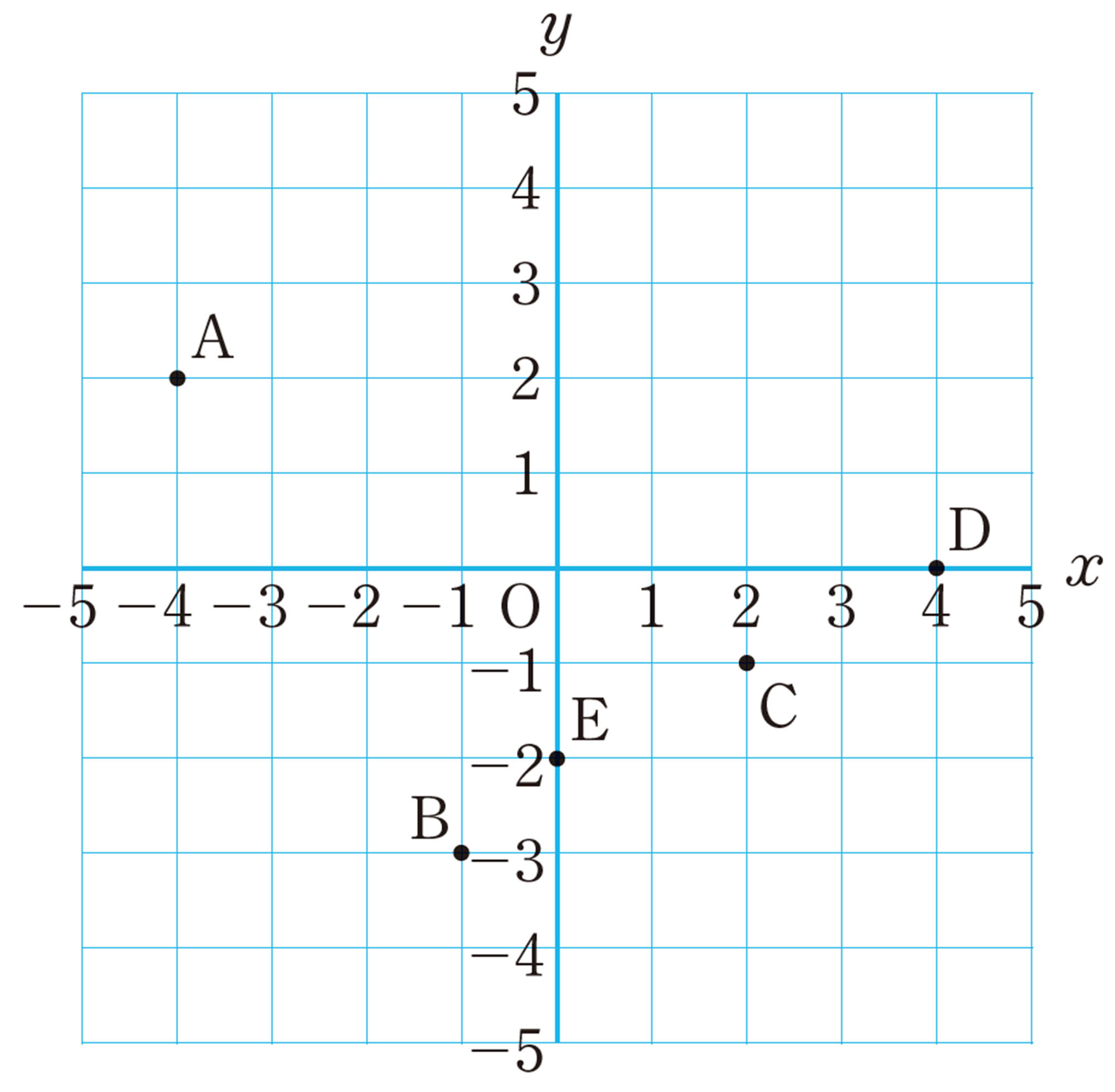
問 １ 点 [mathjax]\(B(3，2)\)を，上の図にかき入れなさい。
問 ２ 右の図で，点 A，B，C，D，E の座標をいいなさい。
問 ３ 次の点を，右の図にかき入れなさい。
[mathjax]\(P(1，3)\)
[mathjax]\(Q(-3，4)\)
[mathjax]\(R(-2，-4)\)
[mathjax]\(S(3，-2)\)
[mathjax]\(T(0，2)\)
[mathjax]\(U(-4.5，0)\)
<1年p.142>
比例のグラフ
Q Question
関数[mathjax]\(y=2x\)について，次のような表をつくることができます。関数[mathjax]\(y=2x\)のグラフがどんな形になるか予想してみましょう。
比例のグラフは，原点Oを通る直線だったね。
直線をそのままのばせばいいのかな。
見方・考え方
変域を負の数まで広げたときは，どんなグラフになるかな。
目標 ▷ 変域や比例定数を負の数まで広げたときの比例のグラフについて調べよう。
問 ４ 【Q】の表の対応するx，yの値の組をそれぞれx座標，y座標とする点[mathjax]\((-5，-10)\)，…，[mathjax]\((5，10)\)を，右の図にかき入れなさい。
問 ５ 【Q】で，xの値を[mathjax] \(-5\)から5まで[mathjax]\(0.5\)おきにとり，それらに対応する点を，右の図にかき入れなさい。
より正確なグラフをかくには，どうすればいいのかな。
<1年p.143>
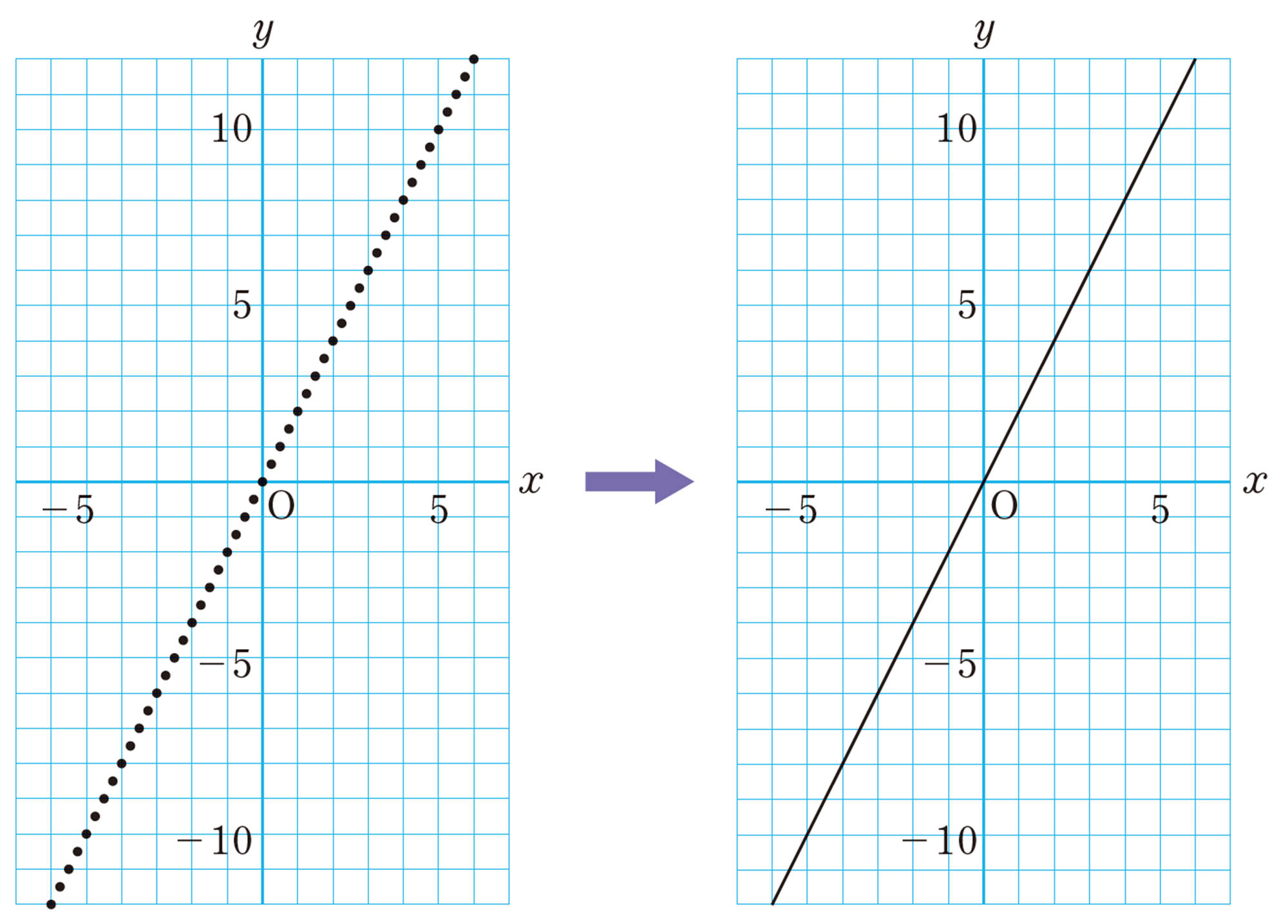
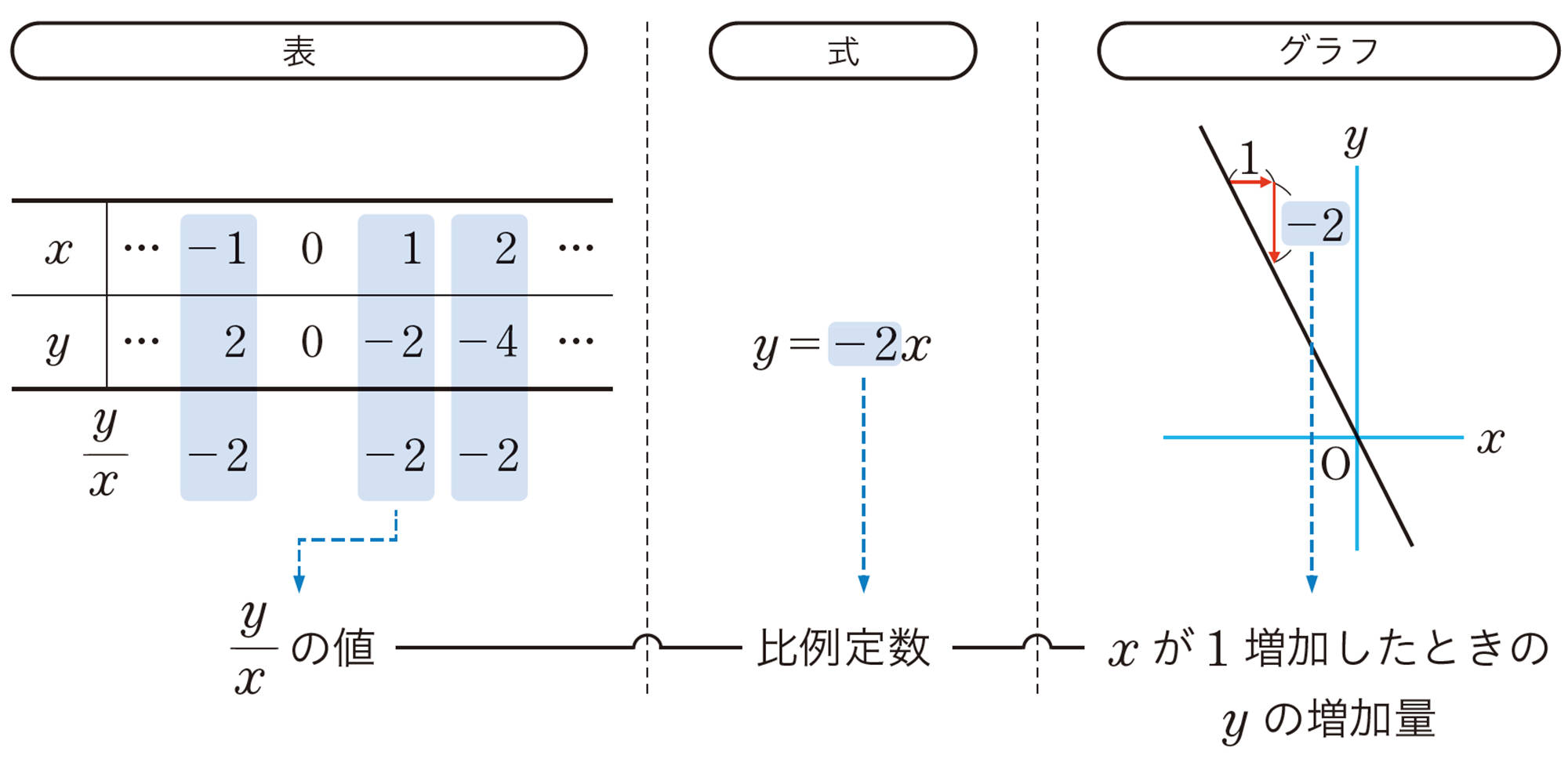
左下の図のように，[mathjax]\(y=2x\)が成り立つx，yの値の組を座標とする点をさらに多くとっていくと，点の集合は右下の図のような直線になることがわかる。
この直線が，関数[mathjax]\(y=2x\)のグラフである。
小学校で学んだ比例のグラフは，座標軸の右上の部分だね。
問 ６ 関数[mathjax]\(y=-2x\)について，次の問いに答えなさい。
⑴ xの値に対応するyの値を求め，次の表にまとめなさい。
⑵ グラフはどんな形になりますか。上の表の対応するx，yの値をそれぞれx座標，y座標とする点を，右上の図にかき入れなさい。
⑶ xの変域をすべての数として，[mathjax]\(y=-2x\)のグラフを，右上の図にかき入れなさい。
<1年p.144>
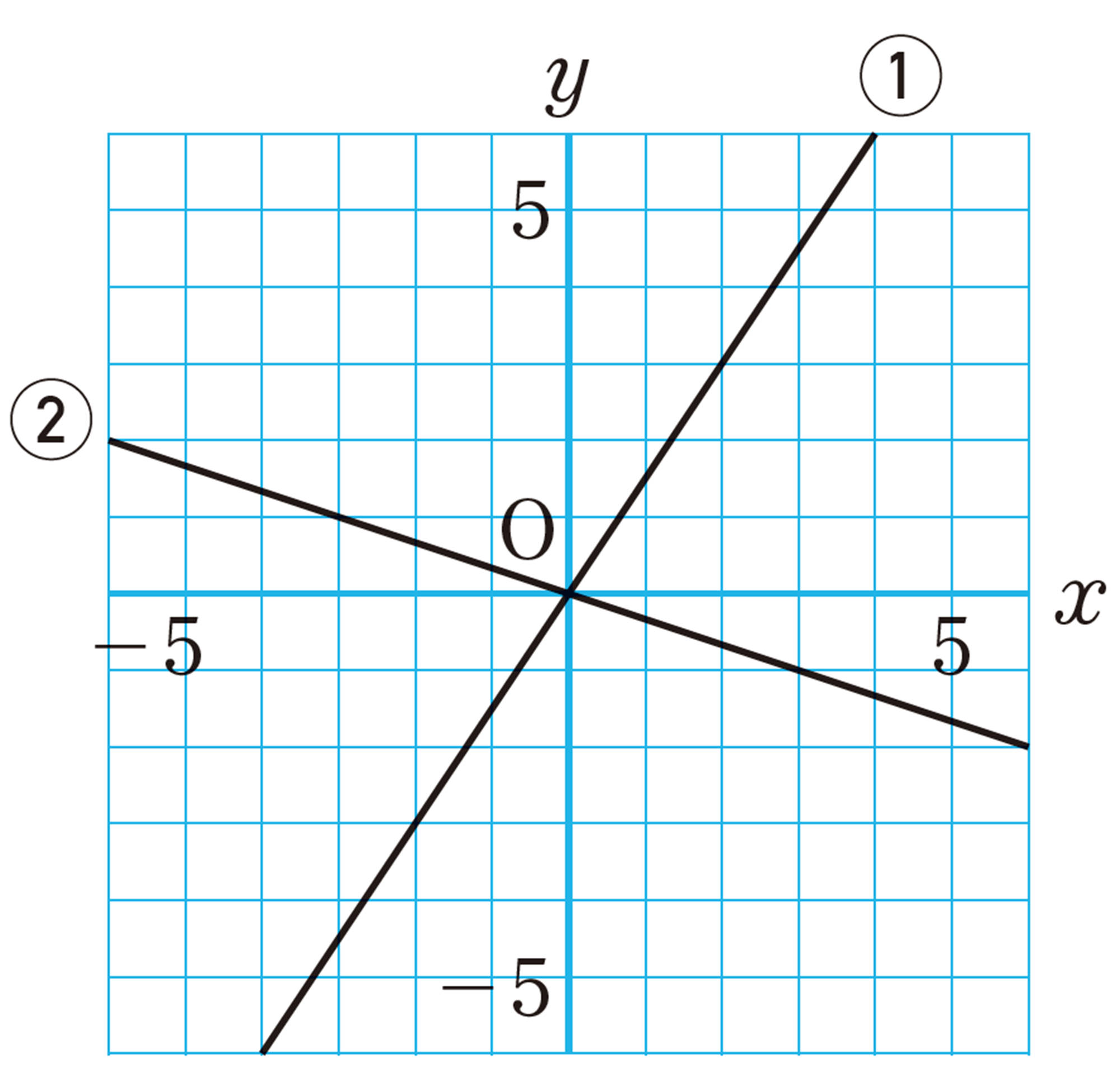
問 7
次の関数について，x，y の対応の表をつくり，グラフを左の図にかき入れなさい。
⑴ [mathjax]\(y=3x\)
⑵ [mathjax]\(y=-3x\)
⑶ [mathjax]\(y=\dfrac{1}{2}x\)
⑷ [mathjax]\(y=-\dfrac{1}{2}x\)
問 ８ 次の問いに答えなさい。
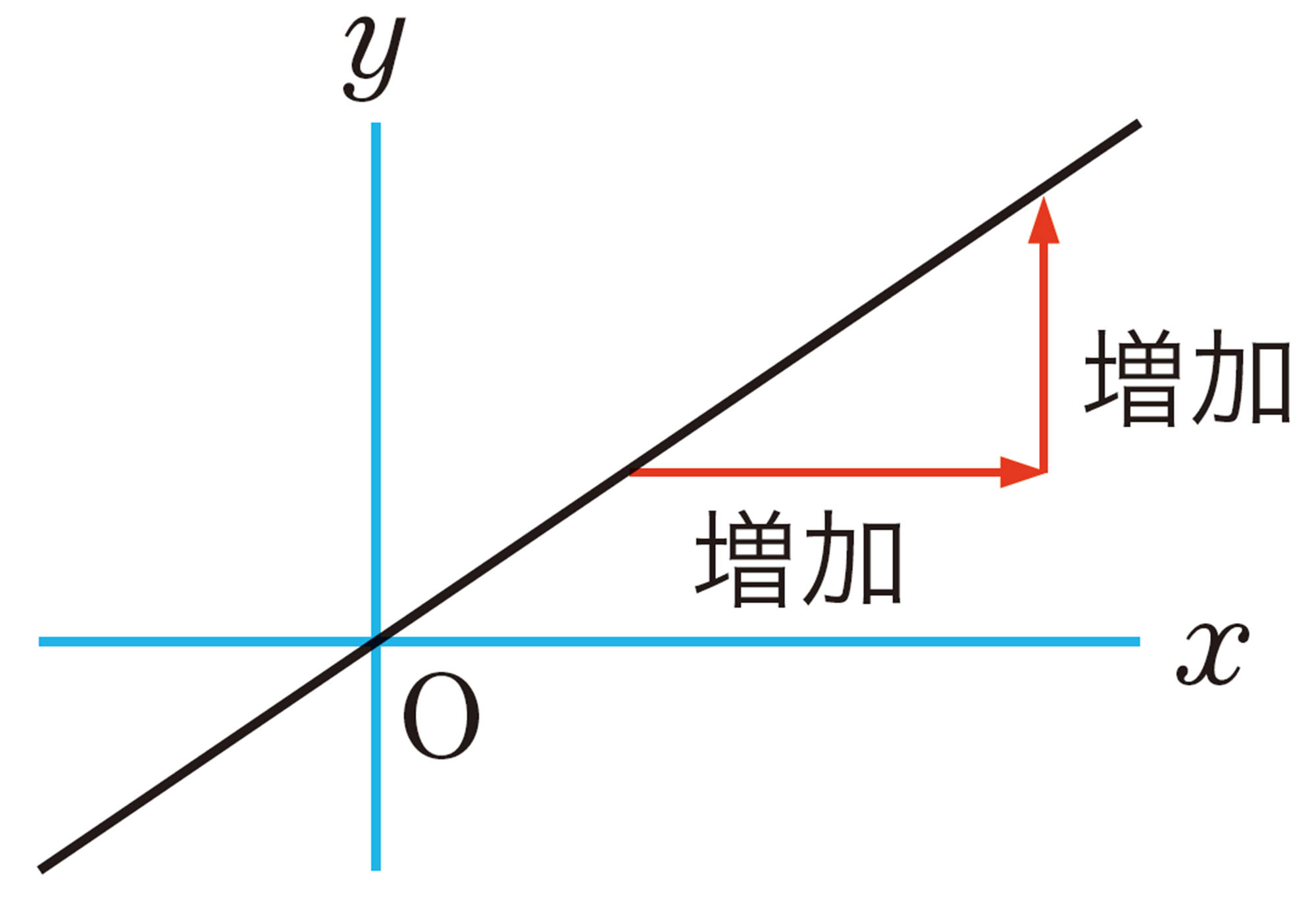
⑴ 関数 [mathjax]\(y=2x\)では，xの値が1増加すると，yの値はどのように変化しますか。表やグラフをもとに説明しなさい。
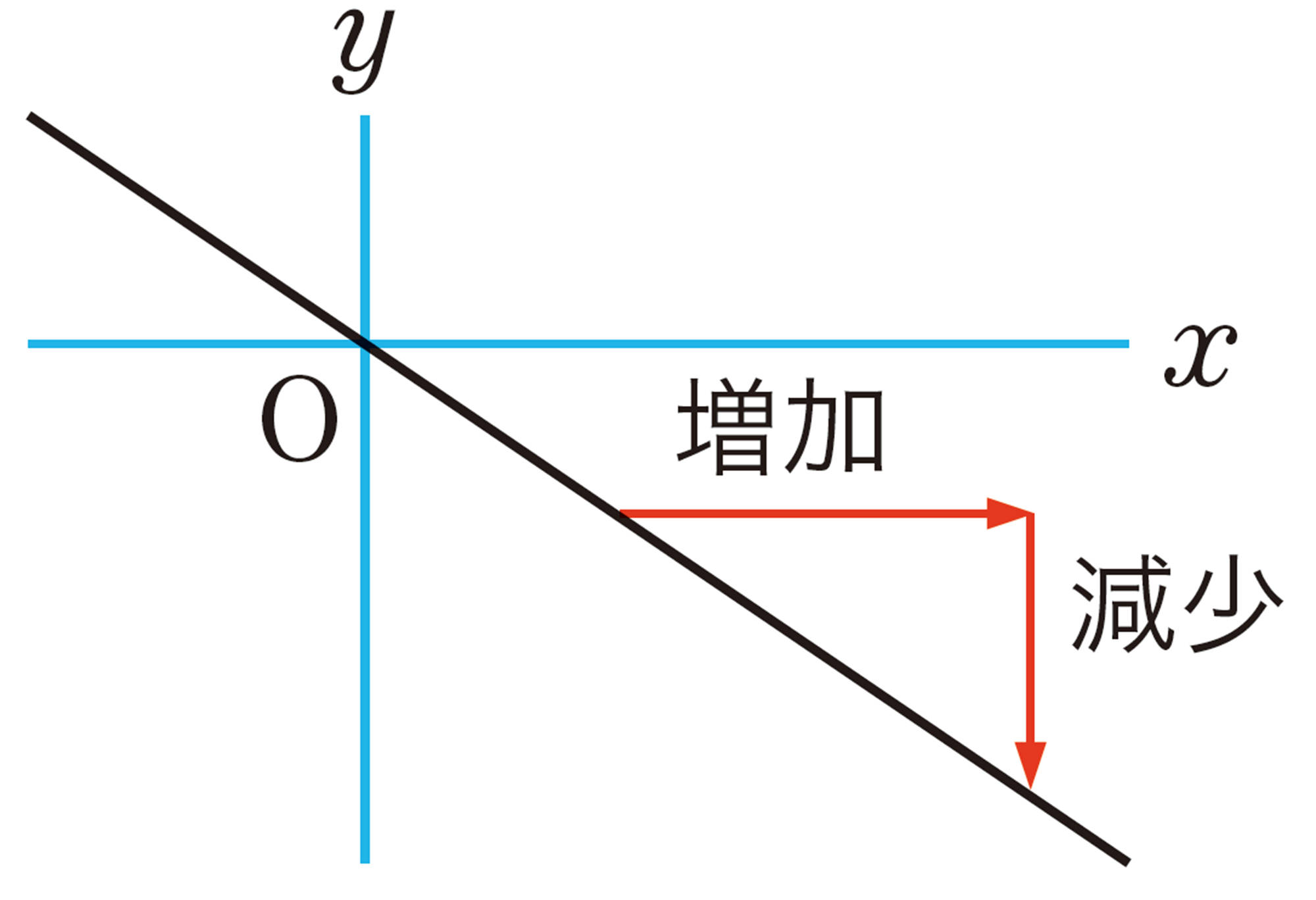
⑵ 関数 [mathjax]\(y=-2x\)について，⑴と同じことを調べなさい。
⑶ ⑴ ，⑵で調べたことや，問7でかいたグラフから，関数 [mathjax]\(y=ax\)のグラフについて，比例定数aが正の数のときと負の数のときで，共通するところや異なるところをいいなさい。
これまで調べたことから，比例のグラフについて，次のようにまとめることができる。
比例のグラフ
比例を表す関数[mathjax]\(y=ax\)のグラフは，原点を通る直線である。
① [mathjax]\(a \gt 0\)のとき，右上がり
xの値が増加すると，
yの値も増加する。
② [mathjax]\(a \lt 0\)のとき，右下がり
xの値が増加すると，
yの値は減少する。
<1年p.145>
関数[mathjax]\(y=-2x\)を例として，比例の表，式，グラフの関係を示すと，次のようになる。
比例のグラフは，原点を通る直線であるから，原点とそれ以外の1つの点がわかればかくことができる。
例 １ 関数[mathjax]\(y=\dfrac{2}{3}x\)は，[mathjax]\(x=3\)のとき，[mathjax]\(y=2\)であるから，そのグラフは原点[mathjax]\((0，0)\)と点[mathjax]\((3，2)\)を通る直線をかけばよい。
問 ９ 次の関数のグラフを，原点とそれ以外の 1つの点を決めて，右の図にかき入れなさい。
⑴ [mathjax]\(y=\dfrac{1}{4}x\)
⑵ [mathjax]\(y=-\dfrac{5}{2}x\)
グラフをかいたあと，グラフ全体が正しい点を通っているか確認しよう。
<1年p.146>
問 10 右の図について，次の問いに答えなさい。
⑴ 比例のグラフ①が点[mathjax]\((2，3)\)を通ることを利用して比例定数を求め，yをxの式で表しなさい。
⑵ 比例のグラフ②について，yをxの式で表しなさい。
どんなことがわかったかな
比例のグラフは，変域を負の数まで広げても直線になり，比例定数が正の数のとき右上がり，負の数のとき右下がりになります。
次の課題へ！
反比例も比例と同じように，変域や比例定数を負の数まで広げて考えられるのかな？
P.147
確かめよう 2節 比例
１ 底辺12 cm，高さx cmの三角形の面積をy cm²とするとき，次の問いに答えなさい。
⑴ yをxの式で表しなさい。
⑵ yはxに比例するといえますか。
２ yはxに比例し，[mathjax]\(x=4\)のとき[mathjax]\(y=12\)です。yをxの式で表しなさい。また，[mathjax]\(x=-6\)のときのyの値を求めなさい。
３ 右の図で，点 A の座標をいいなさい。また，点[mathjax]\(B(3，-1)\)を，右の図にかき入れなさい。
４ 関数[mathjax]\(y=-x\)のグラフを，右の図にかき入れなさい。
５ 右の①のグラフについて，yをxの式で表しなさい。
