<1年p.128>
ふりかえり 〜算数から数学へ〜
【比例】
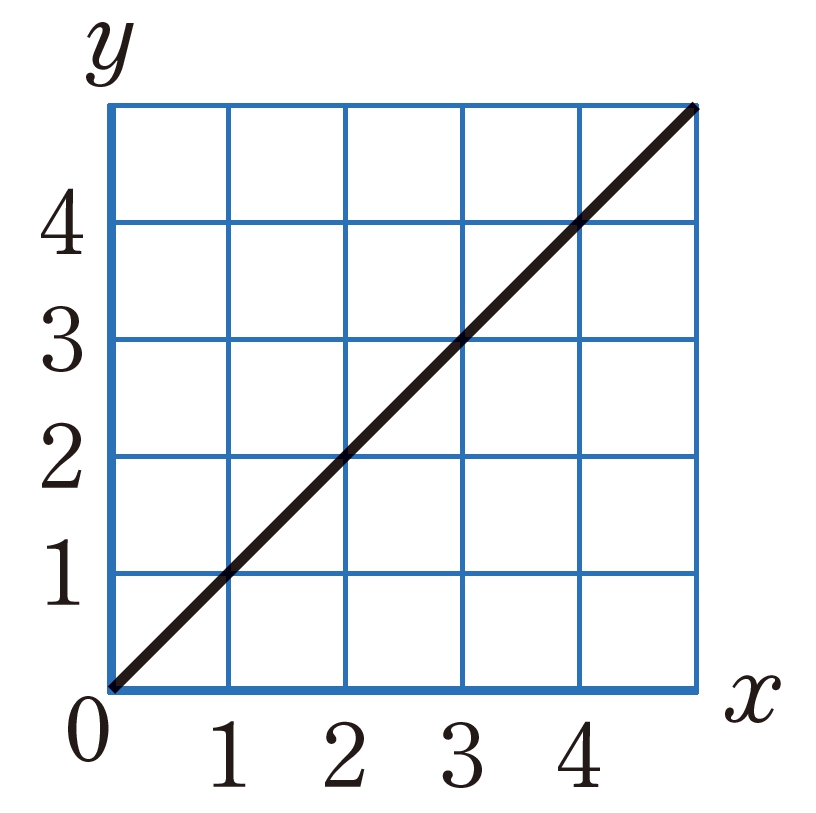
ともなって変わる2 つの量x とy があって，x の値が2倍，3倍，…になると，yの値も 2倍，3 倍，…になるとき， y はxに比例するという。
ともなって変わる2つの量について考えるときは，表に表して，きまりを見つけたね。
【比例の式】
2 つの量x とy があって，y がx に比例するとき，この関係を式で表すと，次のようになる。
[mathjax]\(y=\text{決まった数}\times x\)
比例の関係を考えるときは，表，式，グラフといろいろな表し方をしたね。
【比例のグラフ】
比例の関係をグラフに表すと，縦の軸と横の軸が交わる0の点を通る直線になる。
【反比例】
ともなって変わる2 つの量x とy があって， xの値が2 倍，3倍，…になると，yの値は[mathjax]\(\dfrac{1}{2}\)倍，[mathjax]\(\dfrac{1}{3}\)倍，…になるとき， yはx に反比例するという。
【反比例の式】
2 つの量x とy があって，y がx に反比例するとき，この関係を式で表すと，次のようになる。
[mathjax]\(x \times y=\text{決まった数}\)
反比例の関係を考えるときは，比例と比べて，似ているところやちがうところを探したね。
<1年p.129>
４章 Chapter 4 比例と反比例
1節 関数
2節 比例
3節 反比例
4節 比例と反比例の利用
だいぶ水がたまってきたね。
1時間で8cm水位が増加したよ。
1時間前の水位は，今より8cm低いところだったんだね。
1時間前の水位は，どうやって表せばいいのかな。
？ 比例や反比例は負の数でもいえるのかな？
<1年p.130>
1節 関数
ともなって変わる2つの数量の関係は？
縦25 m ，横13 m ，深さ[mathjax]\(1.2\) m のプールがあります。
プール開きの前に，プールをきれいに掃除したあと，一定の割合で，プールが満水になるまで水を入れていきます。
【１】 プールに水を入れるとき，ともなって変わる 2つの数量をいろいろ見つけましょう。
時間にともなって変わる数量はいろいろあるね。
水を入れる時間が変わると，水位が変わるね。
水を入れる時間と水位の関係のグラフは，どんな形になるのかな。
<1年p.131>
【２】 次の ①〜 ③の水そうに一定の割合で水を入れます。
水を入れる時間と水位の関係をグラフに表すと，それぞれ㋐～㋒ のどれになるでしょうか。ただし，水位はいちばん高いところとします。
①
②
③
㋓
㋑
㋒
【３】 右の水そうに一定の割合で水を入れたとき，水を入れた時間と水位の関係をグラフに表すとどうなるでしょうか。およそのグラフをノートにかきましょう。
【４】 身のまわりから，ともなって変わる2つの数量の関係にあるものを探しましょう。
次の課題へ！
ともなって変わる2つの数量の間には，どんな関係があるのかな？
P.132
<1年p.132>
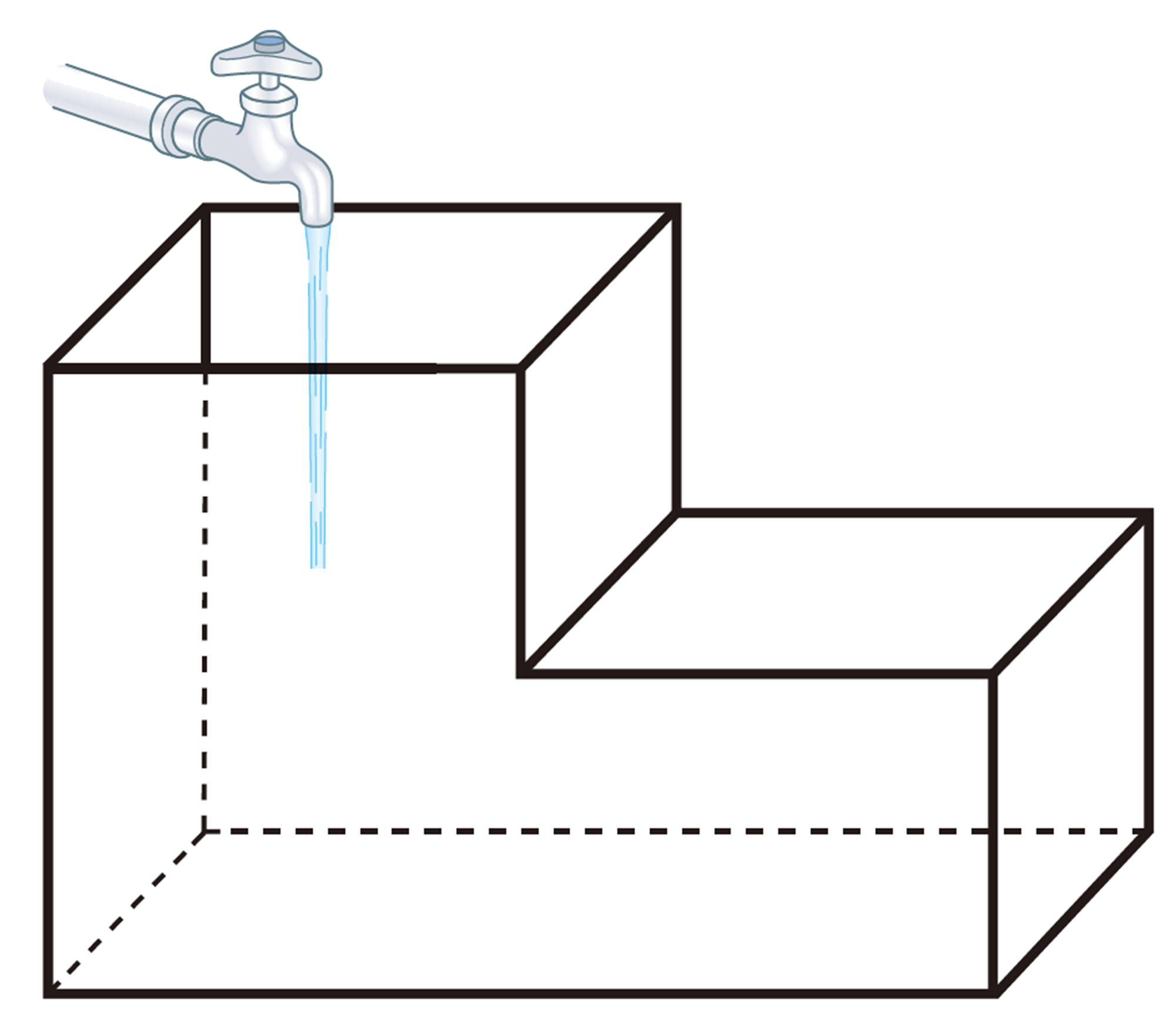
１ 関数
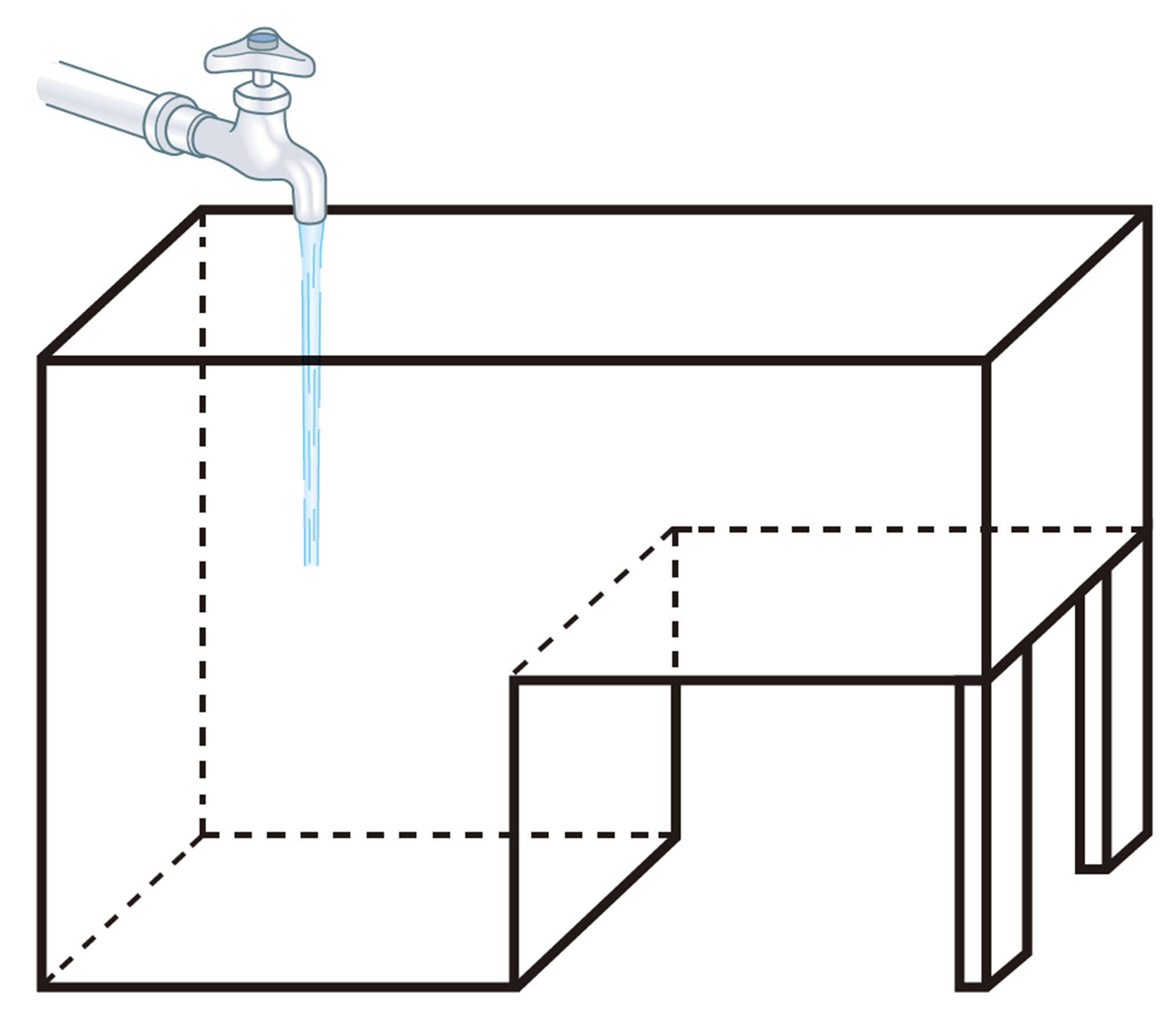
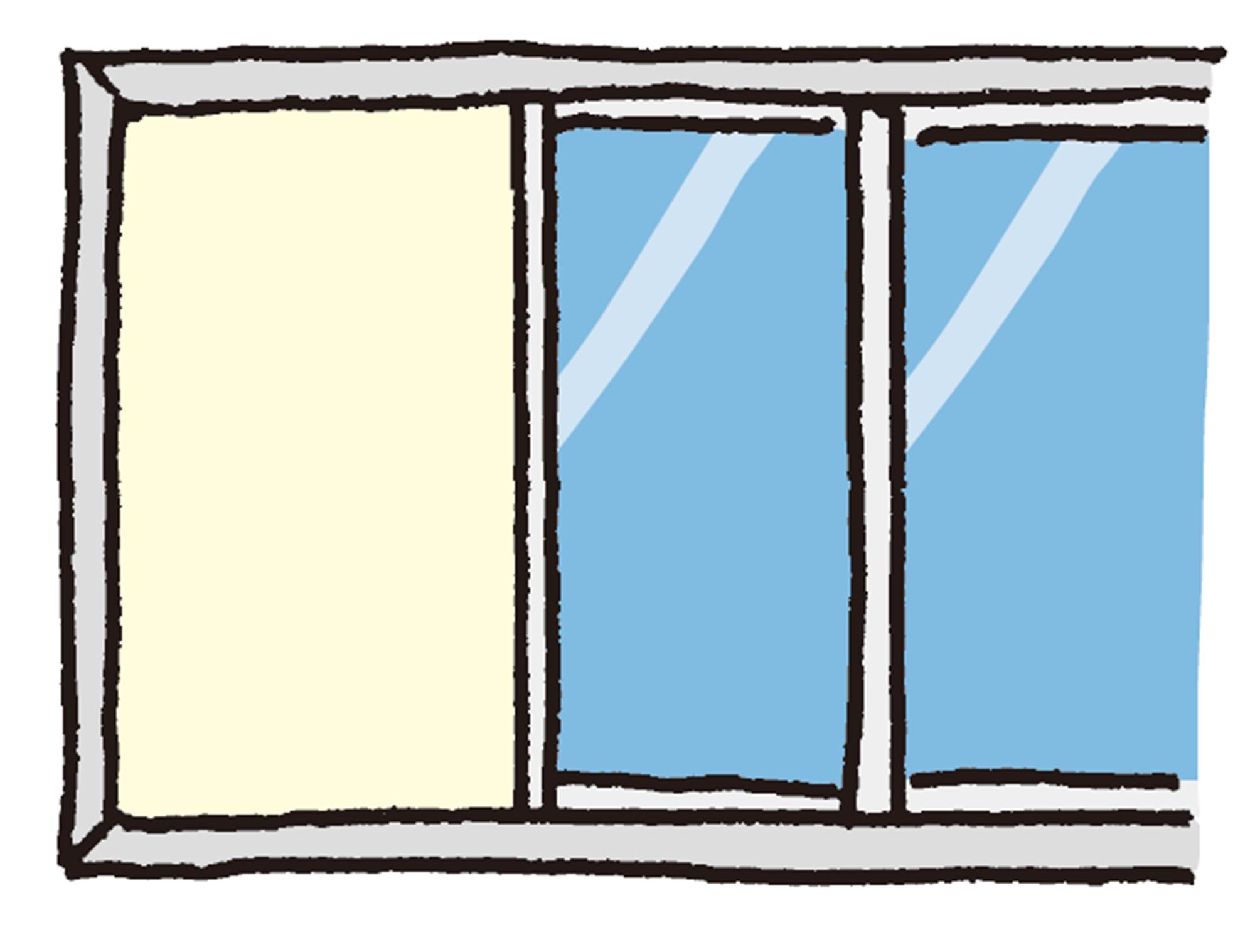
Q Question
縦90 cm の長方形の窓をx cm 開けたとき，開けた部分の周囲の長さをy cm とします。xとyの関係を，次の表にまとめてみましょう。
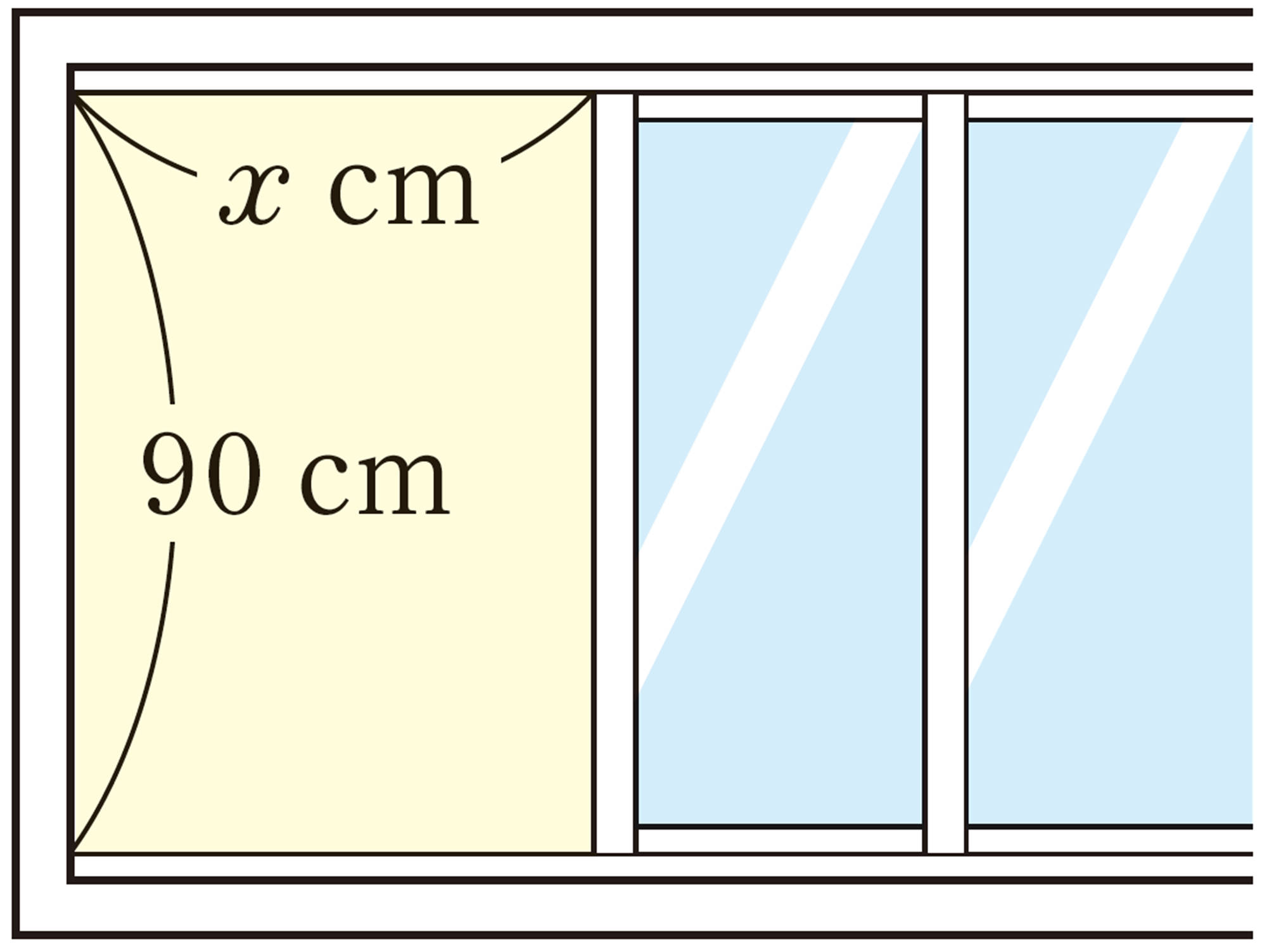
xが増えると，yも増えていくね。
xの値を決めると，yの値はいつでも決まるのかな。
見方・考え方
2つの数量にどんな関係があるか見つけられるかな。
目標 ▷ ともなって変わる2つの数量の関係について調べよう。
【Q】のx，yのように，いろいろな値をとる文字を 変数 という。
【Q】のように，ともなって変わる2つの変数x，yがあって，xの値を決めると，それに対応するyの値がただ1つ決まるとき，yはxの関数である という。【Q】 では，周囲の長さは開けた幅の関数である。
関連 ▷ p.134
例 １
⑴ 【Q】で，窓をx cm 開けたときの開けた部分の面積をy cm²とする。このとき，xの値を決めると，それに対応するyの値がただ1つ決まるから，yはxの関数である。
⑵ x歳の人の身長をy cm とする。このとき，xの値を決めても，それに対応するyの値がただ1つに決まらないから，yはxの関数ではない。
問 １ 次の⑴～⑶ で，yはxの関数であるといえますか。
⑴ 1辺の長さがx cm の正方形の面積はy cm² である。
⑵ まわりの長さがx cm の長方形の面積はycm² である。
⑶ 14L の灯油をxL 使ったとき，残りはyL である。
<1年p.133>
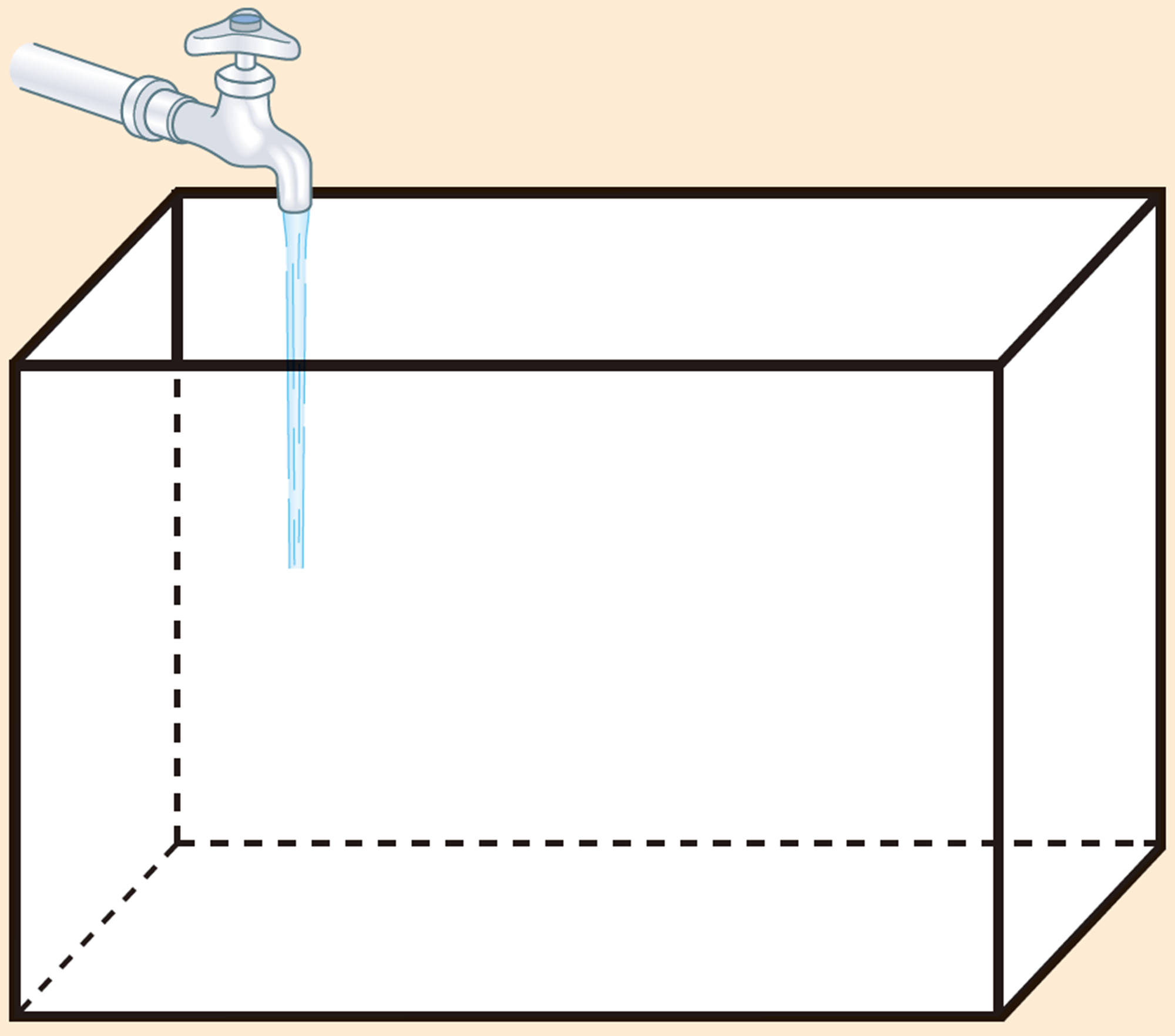
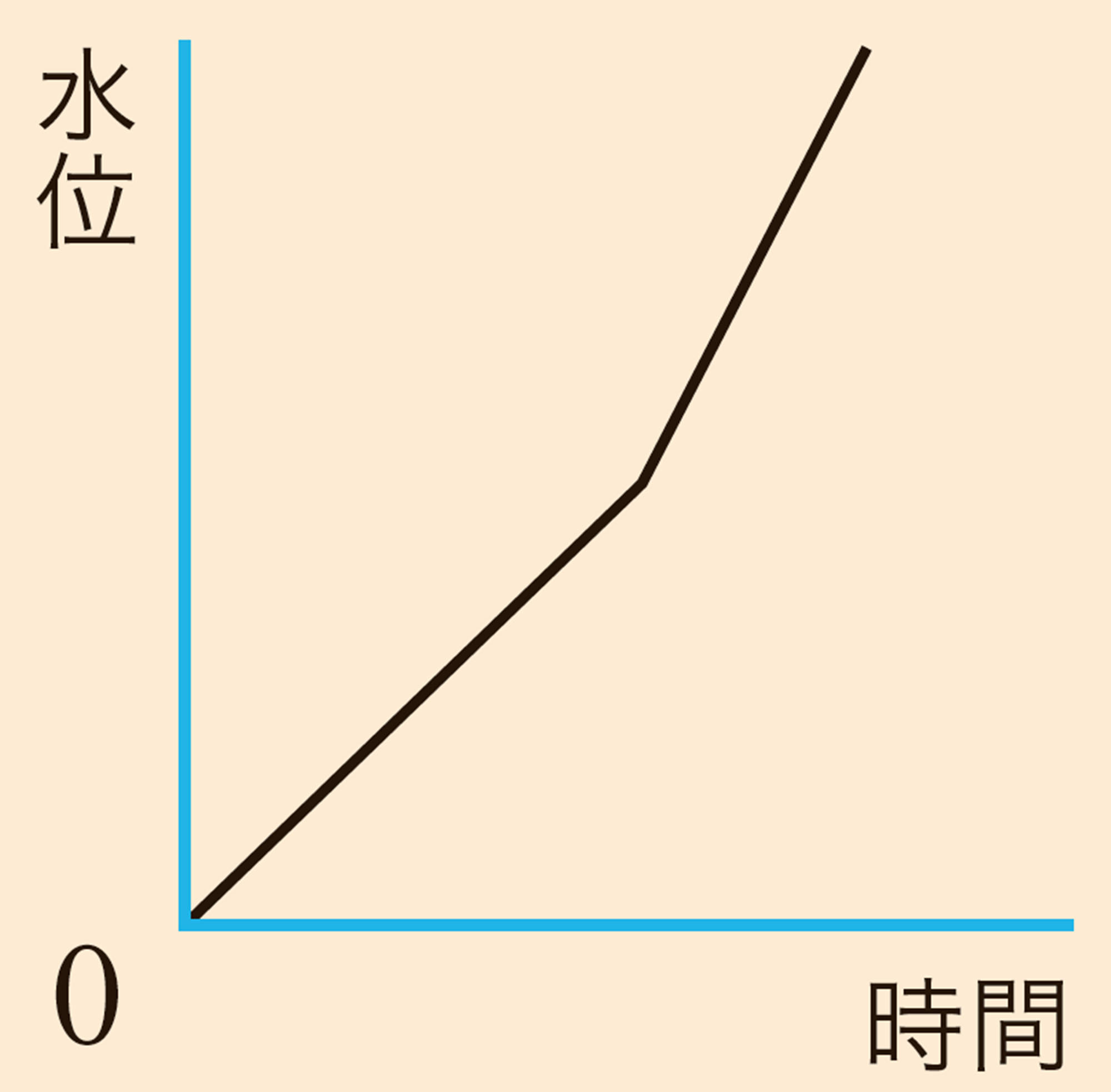
問 ２ 深さ[mathjax]\(1.2\) m のプールに，1時間に8 cm ずつ水位が増加するように一定の割合で水を入れます。水を入れ始めてからx時間後の水位をy cmとするとき，次の問いに答えなさい。
⑴ xとyの関係を，次の表にまとめなさい。
⑵ yはxの関数であるといえますか。
⑶ yをxの式で表しなさい。また，xとyはどんな関係といえますか。
⑷ プールが満水になるのは，水を入れ始めてから何時間後ですか。
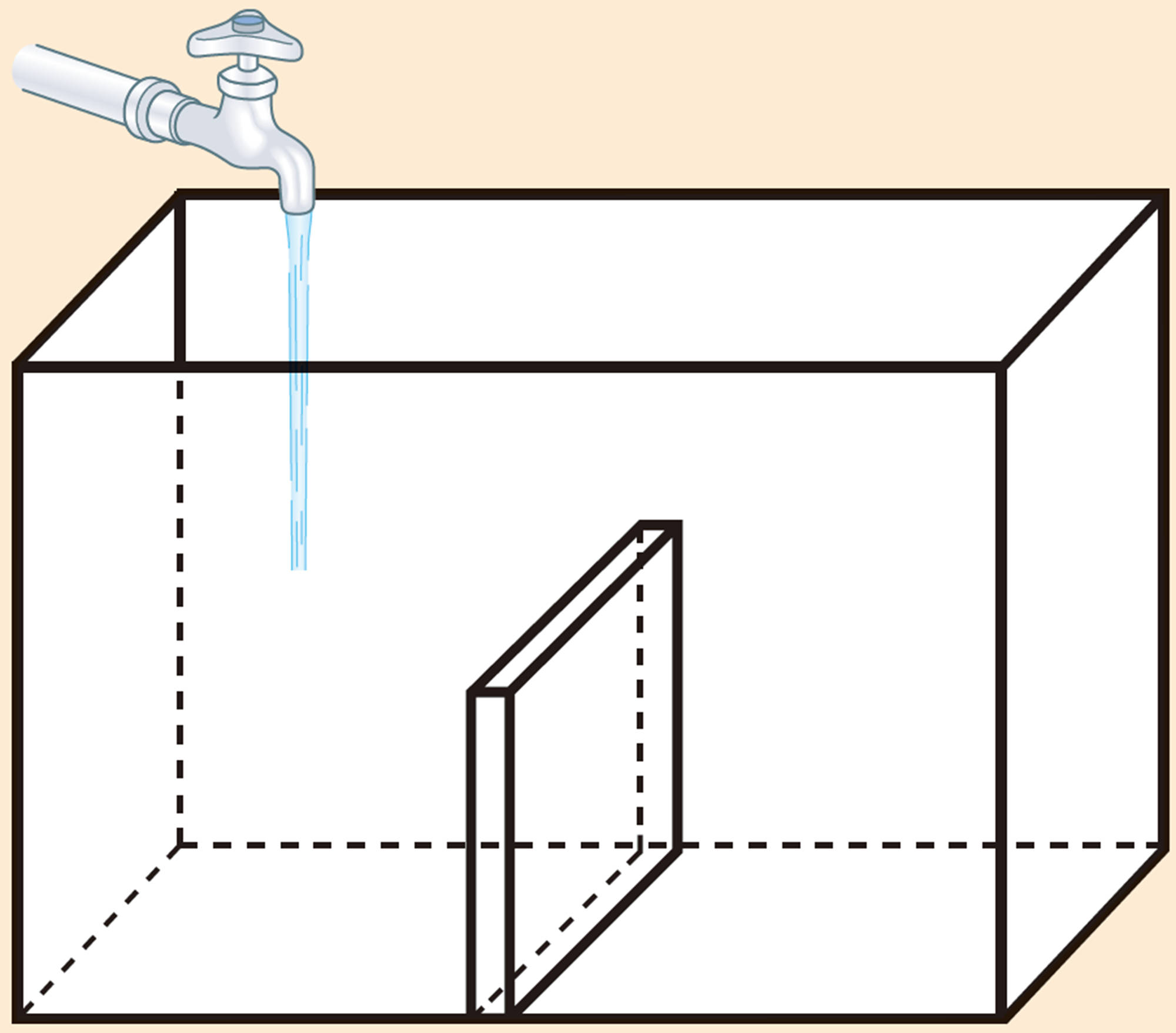
問 ３ 問2のプールに，1時間にx cm ずつ水位が増加するように水を入れると，y時間で満水になりました。このとき，次の問いに答えなさい。
⑴ xとyの関係を，次の表にまとめなさい。
⑵ yはxの関数であるといえますか。
⑶ yをxの式で表しなさい。また，xとyはどんな関係といえますか。
問2や問3は，xの値を決めると，それに対応するyの値がただ1つ決まる。このように，小学校で学んだ比例や反比例も関数であるといえる。
問2の場合，プールは15時間で満水になる。すなわち，水を入れ始めてからの時間xの範囲は，0以上15以下である。このような，変数のとる値の範囲を，その変数の 変域 という。
xの変域が0以上15以下であることは，次のように，不等号を使って表したり，数直線を使って表したりする。
[mathjax]\(0 \leqq x \leqq 15\)
注意 特に指定がないときの変域は，すべての数になる。
<1年p.134>
問 ４ 前ページの問2のx，y の関係で，y の変域を不等号を使って表しなさい。
問 ５ 次のそれぞれの場合について，xの変域を不等号を使って表しなさい。
⑴ xの変域が[mathjax] \(-10\)以上である。
⑵ xの変域が30未満である。
⑶ xの変域が[mathjax] \(-10\)以上30未満である。
注意 変域を数直線上に表すとき，● はその数をふくむことを，◯ はその数をふくまないことを意味する。
どんなことがわかったかな
ともなって変わる2つの数量x，yで，xの値を決めるとyの値がただ1つ決まるとき，yはxの関数であるといえます。
次の課題へ！
比例や反比例で，変数や変域を負の数にしてもいいのかな？
P.135
確かめよう 1節 関数
□ 関数，変域について理解している。 関数 P.132問1P.134問4
１ 長さ10 m のテープをx m 使った残りをy m とするとき，次の問いに答えなさい。
⑴ [mathjax]\(x=2\)のときのyの値を求めなさい。
⑵ yはxの関数であるといえますか。
⑶ x の変域が [mathjax]\(0 \leqq x \leqq 7\)のときのyの変域を求めなさい。
用語の由来「関数」 Tea Break
「関数」は，英語の「function」の訳です。「function」には，“機能”や“働き”という意味があります。
「function」の「fun」は，中国語の「函」の発音と似ているため，中国では「函数」という用語を使い，「ファンスウ」と発音しています。日本でも以前は「函数」と書いていましたが，使用漢字の制限で，「関数」に改められました。「関」には，“かかわる”という意味があり，「関数」は，数量の関係を表す用語と解釈することができます。
