<1年p.124>
３章のまとめの問題 解答 P.304 基本
１ 次の数量の関係を，等式や不等式で表しなさい。
⑴ 1個x円のりんご10個と200円のかごの代金の合計は1300円である。
⑵ ある数xを2倍して3をひくと，xに5を加えた数より大きくなる。
２ 方程式[mathjax]\(3x-5=7\)を次のようにして解きました。左下の①，②の操作には，それぞれどんな等式の性質が使われていますか。右下の㋐～㋓の中から選びなさい。また，そのときのmの値をいいなさい。
㋐ [mathjax]\(A=B\)ならば，[mathjax]\(A+m=B+m\)
㋑ [mathjax]\(A=B\)ならば，[mathjax]\(A-m=B-m\)
㋒ [mathjax]\(A=B\)ならば，[mathjax]\(Am=Bm\)
㋓ [mathjax]\(A=B\)ならば，[mathjax]\(\dfrac{A}{m}=\dfrac{B}{m} \quad (m \neq 0)\)
３ 次の方程式や，比例式を解きなさい。
⑴ [mathjax]\(\dfrac{1}{7}x=4\)
⑵ [mathjax]\(3+4x=-9\)
⑶ [mathjax]\(8x=-3x+11\)
⑷ [mathjax]\(7x-9=8x\)
⑸ [mathjax]\(3x-7=x+5\)
⑹ [mathjax]\(1-6x=4x-9\)
⑺ [mathjax]\(-2(x+3)=9-4x\)
⑻ [mathjax]\(0.6x-1=-0.7\)
⑼ [mathjax]\(\dfrac{1}{2}x+3=\dfrac{3}{4}x-2\)
⑽ [mathjax]\(5 : 2=20 : x\)
⑾ [mathjax]\(8 : x=6 : 21\)
⑿ [mathjax]\(4 : 9=x : 15\)
４ 次の問題について，下の問いに答えなさい。
兄は弟よりも3歳年上で，兄弟の年齢の和は21です。兄と弟の年齢はそれぞれ何歳ですか。
⑴ 大和さんは，この問題を解くのに次のような方程式をつくりました。何をxで表したのかを答えなさい。
[mathjax]\(x+(x-3)=21\)
⑵ ⑴ の方程式を解いて，この問題の答えを求めなさい。
<1年p.125>
５ 水そう A には水が29L ，水そう B には水が10L 入っていました。いま， A からある量だけ水をくんで B に移したところ，A の水の量が B の水の量の2倍になりました。移した水の量を求めなさい。
６ 3 時間で510個の製品をつくる機械があります。この機械を何時間作動させれば850個の製品をつくることができますか。
応用
１ 次の方程式を解きなさい。
⑴ [mathjax]\(5x-2(x+3)=3(1-4x)\)
⑵ [mathjax]\(0.15x-0.3=0.2x-1\)
⑶ [mathjax]\(0.3(x-2)=0.2x+1\)
⑷ [mathjax]\(\dfrac{1}{4}x-\dfrac{1}{3} = \dfrac{2}{3}x + \dfrac{1}{2}\)
⑸ [mathjax]\(\dfrac{x+3}{2} = \dfrac{x-3}{5}\)
⑹ [mathjax]\(x + \dfrac{x-1}{2}=1\)
２ xについての方程式[mathjax]\(3x-a=8\)の解が2のとき，aの値を求めなさい。
３ A 市と B 市の間を自動車で往復しました。行きは時速40km，帰りは時速60km で走り，往復で5時間かかりました。A 市とB 市の間の道のりを求めなさい。
４ 真央さんは，ある店で1個150円の品物を何個か買う予定でしたが，2割引きセールを行っていたため，同じ金額で予定より4 個多く買うことができました。真央さんがこの店で支払った金額を求めなさい。
<1年p.126>
3章のまとめの問題 活用
１ 食料を生産地から食卓まで輸送するとき，フード・マイレージという考え方を使うことがあります。たとえば，1 t の食料を1 km 運ぶとき，フード・マイレージは1 tkm (トンキロメートル)と表します。食料を輸送するとき，トラックや船などの輸送手段を利用しますが，輸送時のフード・マイレージが少ないほど，二酸化炭素排出量が減ります。
二酸化炭素は地球温暖化への影響が大きいと考えられているため，フード・マイレージが少ないほど環境によいと考えられます。
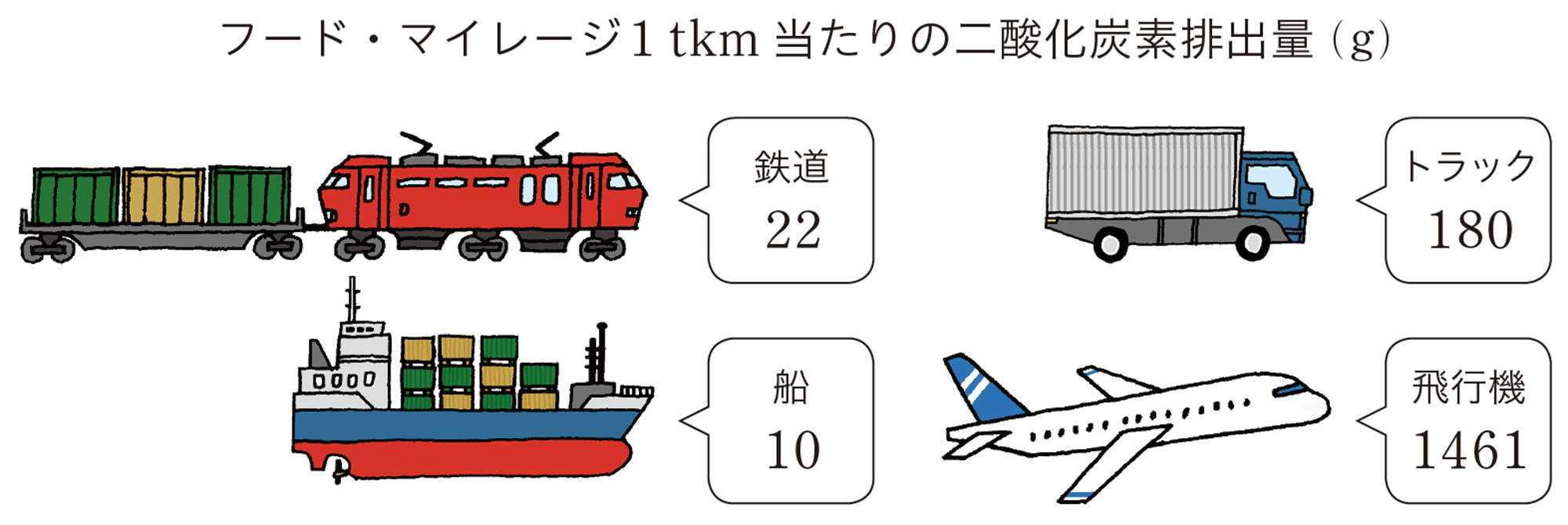
次の図は，フード・マイレージ1 tkm 当たりの二酸化炭素排出量を，輸送手段ごとにまとめたものです。下の⑴〜⑶ の問いに答えなさい。
⑴ 北海道で生産された小麦粉1 kg を，897 km 離れた東京までトラックで輸送します。このときの二酸化炭素排出量は約何gですか。小数第一位を四捨五入して求めなさい。
⑵ アメリカから日本までの輸送距離が10448 km のとき，トラックと船を使って小麦粉10 t を輸入すると，二酸化炭素排出量は3707 kg でした。このとき，トラックと船それぞれの輸送距離を求めなさい。
⑶ 二酸化炭素排出量について考えたとき，次の㋐〜㋒の中から正しいものを選びなさい。
㋐アメリカの小麦粉の方が日本の小麦粉よりも安いから，アメリカから輸入する方がよい。
㋑同じ量の小麦粉を運ぶ場合，トラックよりも鉄道で運ぶ方がよい。
㋒飛行機の方が船よりも輸送時間が短いから，飛行機で運ぶ方がよい。
<1年p.127>
深めよう カーボンニュートラルを目指して
今，多くの自治体で，温室効果ガスの排出を全体としてゼロにする，カーボンニュートラルを目指すとりくみをしています。
「排出を全体としてゼロにする」というのは，二酸化炭素をはじめとする温室効果ガスの「排出量」から，植林，森林管理などによる「吸収量」をひいて，合計を実質的にゼロにすることを意味しています。
カーボンニュートラルの達成のためには，温室効果ガスの排出量の削減，ならびに吸収量を増やすとりくみを強化する必要があります。
札幌市では，2050年までに温室効果ガス排出量を実質ゼロにすることを目標にしています。また，2030年までに，温室効果ガス排出量を2016年の55％削減し，537万 t にすることを目標にしています。
① 2016年の温室効果ガス排出量を求めてみましょう。
② 2016年以降，温室効果ガス排出量を毎年，前年の5％ずつ削減していくとすると，2030年の排出量は約何万t になりますか。目標と比べてみましょう。
③ 温室効果ガス排出量を毎年，前年の5％ずつ削減していくとすると，2050年の排出量は約何万 t になりますか。
④ 1 haの面積の森林が1年間に吸収する温室効果ガスの量は，[mathjax]\(8.8\) t といわれています。 ③で求めた2050年の温室効果ガス排出量を吸収するには，森林が約何ha必要になりますか。
⑤ 札幌市の森林の面積は71372 ha (2020年)です。この森林で吸収できる温室効果ガスの量を求めましょう。
森林だけで温室効果ガスを吸収するのは，難しそうだね。
排出量をもっと減らさないといけないのかな。ほかには，どんな対策があるのかな。
