<1年p.118>
２ 比例式
比例式
Q Question
家庭科で，フレンチドレッシングを作ります。2人分作るのに，酢が20mL ，サラダ油が30mL必要です。
⑴ 酢とサラダ油の量を，できるだけ小さな自然数の比で表してみましょう。
⑵ サラダ油が90mLあります。酢は何mL必要でしょうか。
酢は，サラダ油の何倍の量が必要なのかな。
酢とサラダ油の量の比の値がわかればいいのかな。
見方・考え方
2つの数量の関係を簡単に表すには，どうすればいいかな。
関連 技術・家庭科
目標 ▷ 1次方程式を利用して，比の関係を考えよう。
[mathjax]\(a : b\)で表された比で，aをbでわったときの商[mathjax]\(\dfrac{a}{b}\)を，比の値という。 [mathjax]\(a : b\)の比の値[mathjax]\(\dfrac{a}{b}\)は，bをもとにしたとき，aがその何倍であるかを表した数である。
たとえば，【Q】で，[mathjax]\(20 : 30\)の比の値は，
[mathjax]\(\dfrac{20}{30}=\dfrac{2}{3}\)
であるから，酢は，サラダ油の[mathjax]\(\dfrac{2}{3}\) 倍の量が必要であることがわかる。
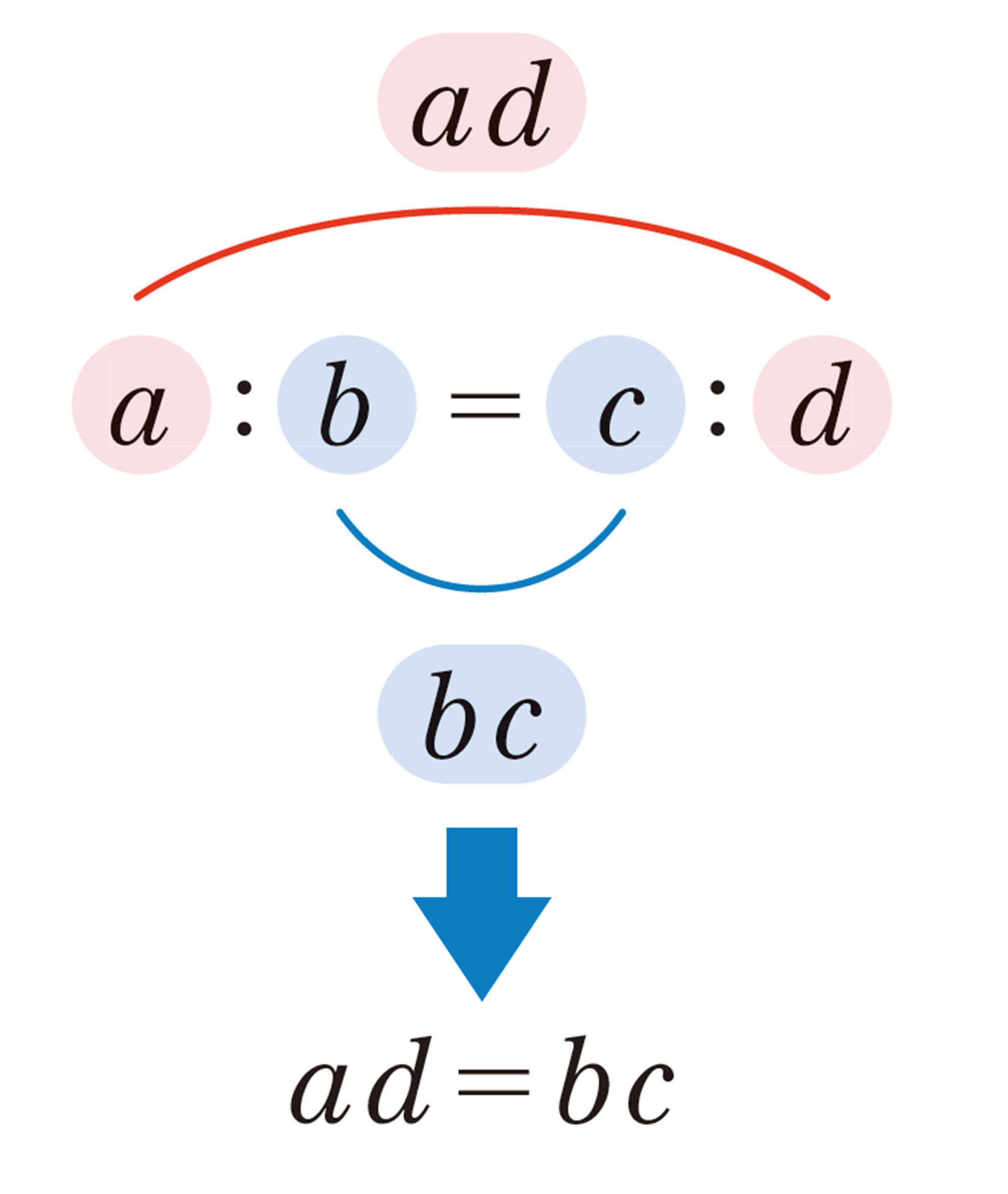
また，2つの比[mathjax]\(a : b\)と[mathjax]\(c : d\)があり，これらの比の値が等しい，すなわち[mathjax]\(\dfrac{a}{b} =\dfrac{c}{d}\) のとき，2つの比は等しいといい，
[mathjax]\(a : b=c : d\)
と表す。このように，2つの比が等しいことを表した式を比例式 という。
問 １ 次の比について，比の値を求めなさい。また，等しい比のものを見つけ，比例式で表しなさい。
⑴ [mathjax]\(3 : 4\)
⑵ [mathjax]\(7 : 5\)
⑶ [mathjax]\(15 : 20\)
⑷ [mathjax]\(6 : 2\)
<1年p.119>
比例式の解き方
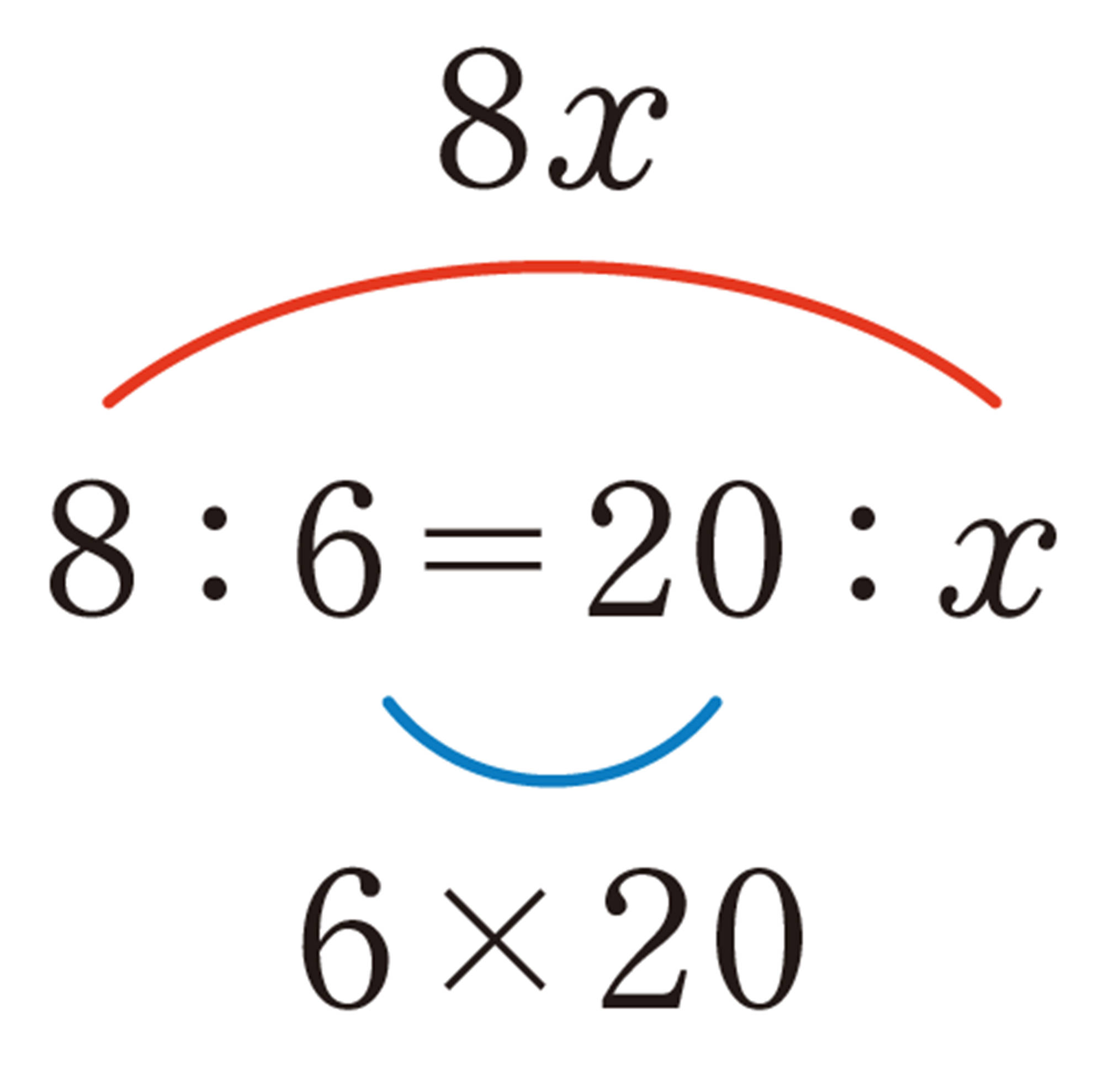
例 １ 比例式[mathjax]\(x : 3=4 : 5\)のxの値を求めなさい。
考え方 両辺の比の値が等しくなることを使い，xの値を求める。
解答
両辺の比の値は等しいから，
両辺に3 をかけると，
答 [mathjax] \(x = \dfrac{12}{5}\)
比例式にふくまれる文字の値を求めることを，比例式を 解く という。
方程式と同じように解けるね。
問 ２ 次の比例式を解きなさい。
⑴ [mathjax] \(x : 9=4 : 3\)
⑵ [mathjax] \(8 : 5=x : 6\)
例1の比例式[mathjax] \(x : 3=4 : 5\)は，次のように解くこともできる。
両辺の比の値は等しいから，
両辺に分母の数3 と5 をかけると，
このとき，上の①の式[mathjax] \(5x=12\)で，
左辺の5xは，比例式の外側の2数，xと5の積，
右辺の12は，比例式の内側の2数，3と4の積
を表している。
問 ３ 問2 の比例式で，外側の2 数の積と内側の2 数の積が等しいことを確かめなさい。
<1年p.120>
一般に，比例式には次の性質がある。
例 ２
[mathjax]\(8 : 6 = 20 : x\)
比例式の性質から，
問 ４ 比例式の性質を使って，次の比例式を解きなさい。
⑴ [mathjax]\(6 : 10=9 : x\)
⑵ [mathjax]\(x : 4=7 : 8\)
⑶ [mathjax]\(\dfrac{1}{3}:x=2×9\)
⑷ [mathjax]\(5 : 8=(x-2) : 16\)
比例式の利用
例 ３ コーヒー120mLと牛乳160mLを混ぜてつくったコーヒー牛乳があります。これと同じ濃さのコーヒー牛乳をつくるとき，コーヒー180mL に対して牛乳何 mL を混ぜればよいですか。
考え方 最初につくったコーヒー牛乳と，これからつくるコーヒー牛乳で，コーヒーと牛乳の量の比は等しいと考えて，その関係を比例式で表す。
解答
混ぜる牛乳の量を[mathjax] \(x\) mL とすると，
コーヒー180 mL に対して牛乳240 mL は，問題に適している。
答 240 mL
[mathjax]\(120 : 160=3 : 4\)と簡単にしてから計算してもいいね。
問 ５ 例3で，牛乳200mL に対しては，コーヒーを何 mL 混ぜればよいですか。
<1年p.121>
問 ６ 高さが2m の棒の影の長さを測ったところ，3m でした。このとき，影の長さが 10m の木の高さは何 m ですか。四捨五入して小数第一位まで求めなさい。
問 ７ [mathjax]\(1 : 100000\)の縮尺の地図上で，A 地点から B 地点までの長さを測ると，4cm でした。A地点からB 地点までの実際の距離は何 km ですか。
どんなことがわかったかな
文字をふくむ比例式は，比例式の性質を利用して方程式をつくれば，方程式と同じように解くことができます。
確かめよう 2節 1次方程式の利用
１ 50円切手と120円切手を合わせて10枚買ったところ，代金の合計が920円になりました。それぞれの切手を何枚買いましたか。代金の関係から方程式をつくり，答えを求めなさい。
２ 折り紙を何人かの生徒に配るのに，1人に2枚ずつ配ると8枚あまり，1人に3枚ずつ配ると4枚たりません。生徒の人数と折り紙の枚数を求めなさい。
３ 比例式[mathjax]\(x : 8=7 : 12\)を解きなさい。
□ 比例式を利用して，問題を解くことができる。 比例式の利用 P.120例3
４ テレビの画面の縦と横の長さの比は[mathjax]\(9:16\)です。画面の縦の長さが50cm のとき，横の長さは約何 cm ですか。小数第二位を四捨五入して求めなさい。
<1年p.122>
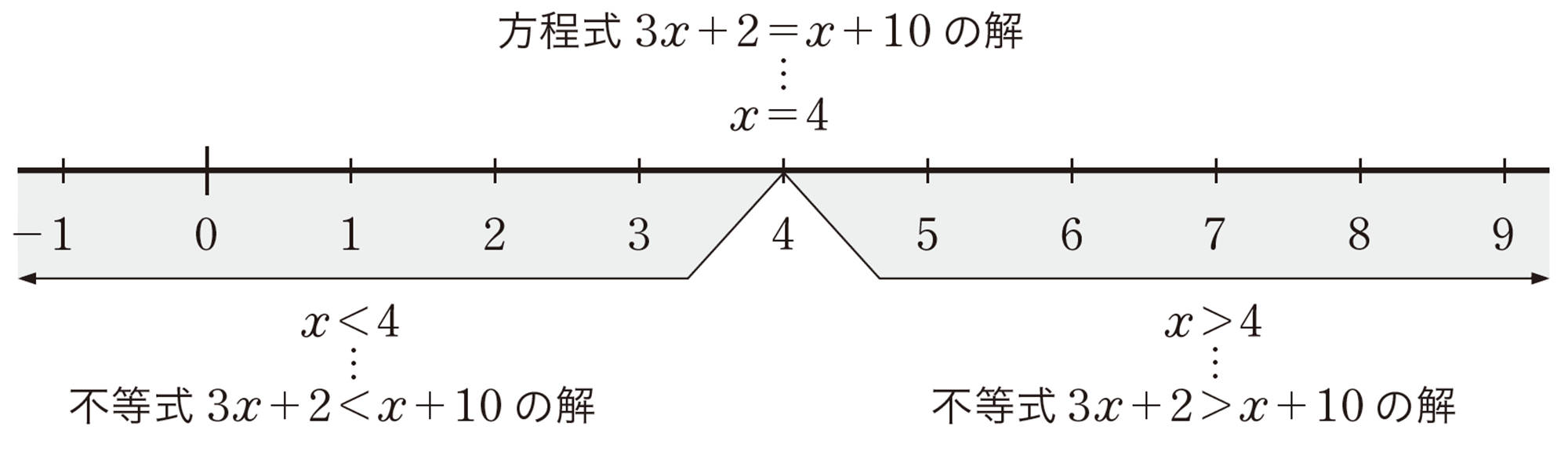
102ページでは，方程式[mathjax]\(3x+2=x+10\)の解を求めるために，両辺のxに 1から5までの整数をそれぞれ代入して，次のような表にまとめ，等式が成り立つかどうかを調べました。
この表から，次のことがわかります。
[mathjax]\(x=1\text{，}2\text{，}3\)のとき， 不等式[mathjax]\(3x+2 \lt x+10\)が成り立つ。
[mathjax]\(x=4\)のとき，方程式[mathjax]\(3x+2=x+10\)が成り立つ。
[mathjax]\(x=5\)のとき，不等式[mathjax]\(3x+2 \gt x+10\)が成り立つ。
方程式を成り立たせるx の値を，方程式の解といったように，不等式を成り立たせるx の値を，不等式の解といいます。
１ 次の①，②について考えてみましょう。
①不等式[mathjax]\(3x+2 \lt x+10\)には， [mathjax]\(x=1，2，3\)以外の解があるでしょうか。
②不等式[mathjax]\(3x+2 \gt x+10\)には，[mathjax]\(x=5\)以外の解があるでしょうか。
1次方程式の解は1つですが，不等式の解は1つとは限りません。
上で調べたことから，方程式[mathjax]\(3x+2=x+10\)の解は，2つの不等式[mathjax]\(3x+2 \lt x+10\)，[mathjax]\(3x+2 \gt x+10\)の解の境目にあることがわかります。xの値を， 0と負の数をふくめたすべての数とするとき，これらの方程式や不等式の解を数直線上に表すと，下のようになります。
この考え方を使えば，不等式の解は，境目となる方程式の解をもとにして求めることができます。
<1年p.123>
3章 「1次方程式」を学んで
できるようになったこと 身のまわりの課題へ P.126，127
数量の関係を等式や不等式で表すことができる。
1次方程式の解の意味を理解し，等式の性質を使って解くことができる。
身のまわりや数学の中から見つけた問題を，1次方程式を使って解決することができる。
さらに学んでみたいこと
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
数学へのいざない 文字を使った式
方程式などで，決まっている数やわからない数を文字を使って表すようになったのは，16世紀から17世紀にかけてのことです。これは，計算に記号が使われるようになって，しばらくしてからのことです。
フランスのフランソワ・ヴィエト（1540〜1603）は，1591年に著した『解析術序論』の中で，決まっている数を表すのに子音文字を，わからない数を表すのに母音文字を使い，体系的な文字記号を導入しました。
その後，フランスのルネ・デカルト（1596〜1650）が1637年に著した『方法序説』の付録『幾何学』の中で，方程式の記号を改良し，現代と同じような形にしました。わからない数を表すのにアルファベットの終わりの方（…，[mathjax] \(x，y，z\)）の文字を使い，決まっている数を表すのにアルファベットの始めの方（[mathjax] \(a，b，c，\)…）の文字を使いました。また，ある量（[mathjax] \(x\)）の係数を文字の左（[mathjax] \(2x\)）に，累乗の指数を右上（[mathjax] \(x²\)）に書く表記もデカルトが始めたことです。
数学は，文字や記号を使うことで，簡潔に表すことができます。
