<1年p.113>
２節 1次方程式の利用
1次方程式が使えるかな？
身のまわりの問題の解決のしかたを考えてみましょう。
【１】 次のような問題を解く手順を考えてみましょう。
1本130円のボールペン2本とノート3冊を買ったところ，代金の合計が710円になりました。ノート1冊の値段は何円でしょうか。
数量の関係を図や表などに表すと，わかりやすくなるかな。
数量の関係を方程式にできるかな。
上のような問題は，次のように方程式を利用して解くことができる。
❶ 図や表，ことばの式などを使って，数量の関係を見つける。
[mathjax]\(\mathsf{(ボールペン2本分の代金)}+\mathsf{(ノート3冊分の代金)}= 710\mathsf{円}\)
❷ 文字を使って方程式をつくる。
ノート1冊の値段をx円とすると，[mathjax]\(130 \times 2+3x = 710\)
❸ 方程式を解く。
上の方程式を解くと，[mathjax]\(x=150\)
❹ 方程式の解が問題に適しているかどうかを確かめ，適していれば問題の答えとする。
ノート1冊150円とすると，ノート3冊分の代金は450円で，合計は710円となり，問題に適している。したがって，ノート1冊の値段は150円である。
次の課題へ！
1次方程式を使って，身のまわりの問題を解決できるかな？
P.114
<1年p.114>
１ 1次方程式の利用
目標 ▷ 1次方程式を利用して，身のまわりの問題を解決しよう。
問 １ 1個240円のケーキ4個と1個90円のプリンを何個か買ったところ，代金の合計が1500円になりました。プリンを何個買ったかを求めるために，前ページの解き方と同じように考えます。次の問いに答えなさい。
⑴ 数量の関係を，図やことばの式で表しなさい。
⑵ ⑴の図やことばの式から，方程式をつくりなさい。
⑶ ⑵でつくった方程式を解きなさい。
⑷ ⑶で求めた方程式の解が問題に適しているかどうかを確かめ，問題の答えを求めなさい。
はじめに図で表すと，数量の関係がわかりやすいね。
例 １ へいを利用して，右の図のような長方形のウサギ小屋をつくります。長さ24m の金網を全部使って，横が縦より3 m 長い小屋をつくるには，縦の長さを何 m にすればよいですか。
考え方 金網の全体の長さと縦，横の長さの関係は，次の図のようになる。
これをことばの式で表すと，[mathjax]\(\mathsf{(縦の長さ)} \times 2 +\mathsf{(横の長さ)}=\mathsf{(全体の長さ)}\)
縦の長さをx m とすると，横の長さはそれより3 m長いから，[mathjax]\((x+3)\) mと表される。これより，数量の関係をもとに，方程式をつくって解けばよい。
解答
縦の長さを [mathjax] \(x\) m とすると，
縦の長さ7 mは， 問題に適している。
答 7 m
問 ２ 長さ150 cm のリボンを姉と妹で分けたところ，姉は妹より30 cm 長くなりました。妹のリボンは何 cm ですか。方程式をつくって求めなさい。
<1年p.115>
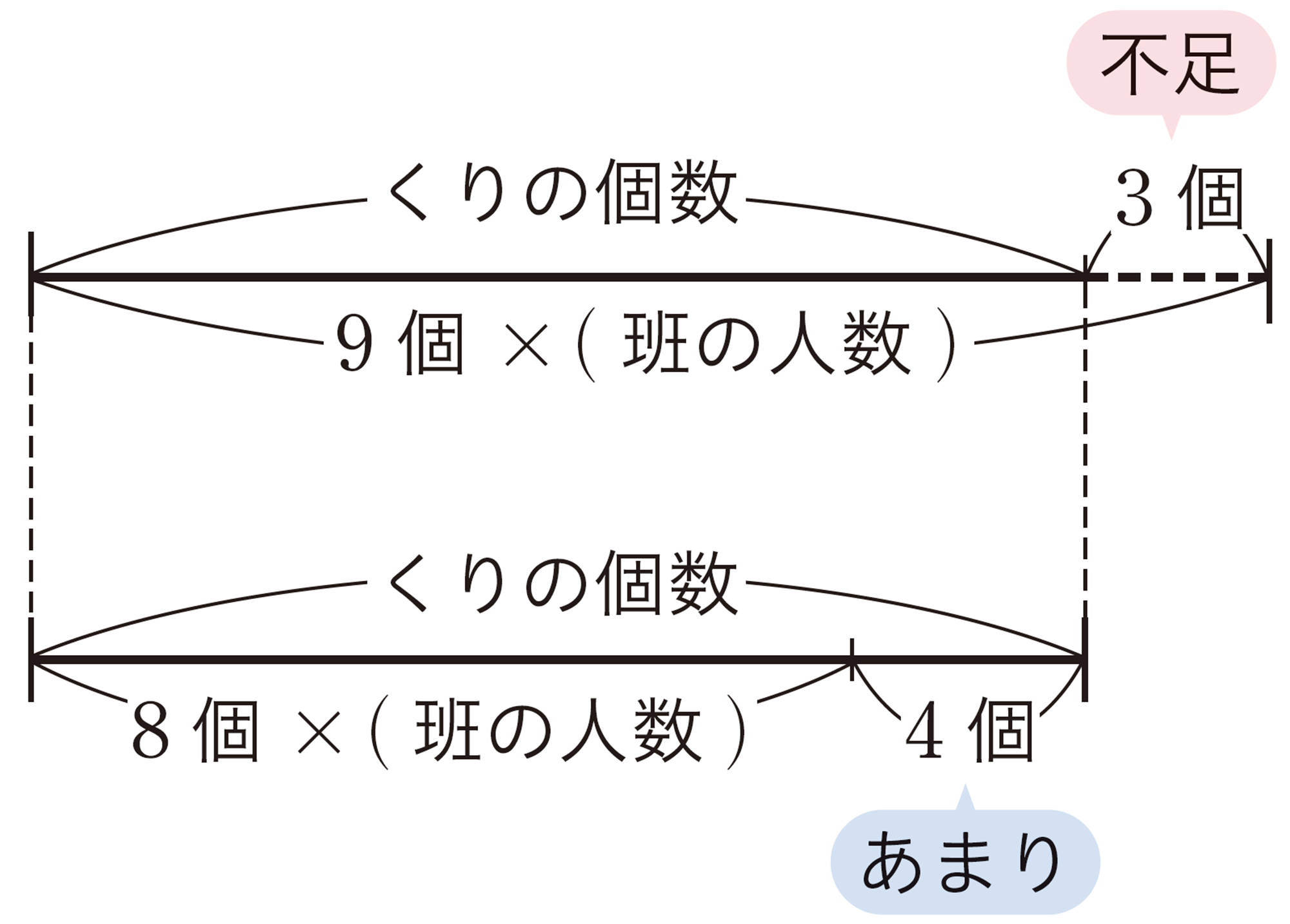
例 ２ 班でくり拾いに出かけ，集めたくりを全員で分けることにしました。1人9個ずつ分けると3個たりません。また，1人8個ずつ分けると4個あまります。班の人数とくりの個数を求めなさい。
考え方 全部のくりの個数が次の㋐，㋑のように2通りで表せることに着目する。
㋐ 1人9個ずつ分けると3個たりないから，くりの個数は，
[mathjax] \(\{9\times \text{(班の人数)}-3\}\)個
㋑ 1人8個ずつ分けると4個あまるから，くりの個数は，
[mathjax] \(\{8 \times\text{(班の人数)}+4\}\)個
この関係をもとに，班の人数をx人として，文字を使って方程式をつくる。
解答
班の人数を [mathjax] \(x\) 人とすると，
くりの個数は，[mathjax] \(9\times 7-3=60\)
班の人数7人，くりの個数60個は，問題に適している。
答 班の人数7 人， くりの個数60 個
問 ３ 例2で，[mathjax] \(x=7\)を[mathjax] \(8x+4\)に代入して，くりの個数が60個であることを確かめなさい。
問 ４ ハンバーガーを7個買おうとしたところ，持っていたお金では80円たりなかったので，6個買ったら130円あまりました。ハンバーガー1個の値段を求めなさい。また，持っていたお金は何円ですか。
▲トライ 例2で，求める2つの数量のうち，くりの個数をx個として方程式をつくり，答えを求めてみよう。
<1年p.116>
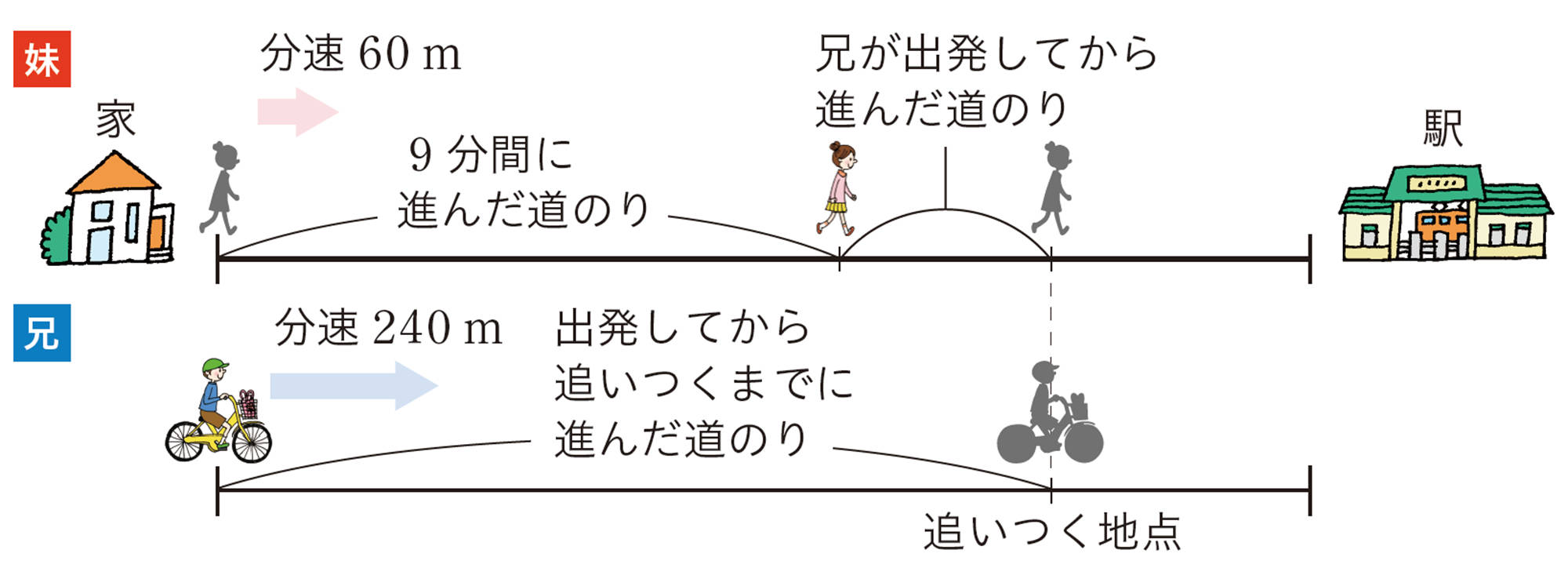
例 ３ 妹は，家から1km 離れた駅に向かって歩いています。妹の忘れ物に気づいた兄は，妹が家を出発してから9分後に，自転車で妹を追いかけました。
妹の速さを分速60m ，兄の速さを分速240mとするとき，兄は出発してから何分後に妹に追いつきますか。
考え方 数量の関係は，次の図のようになる。
上の図から，兄が妹に追いつくとき，次のような関係が成り立つ。
[mathjax]\(\mathsf{(妹が進んだ道のり)}=\mathsf{(兄が進んだ道のり)}\)
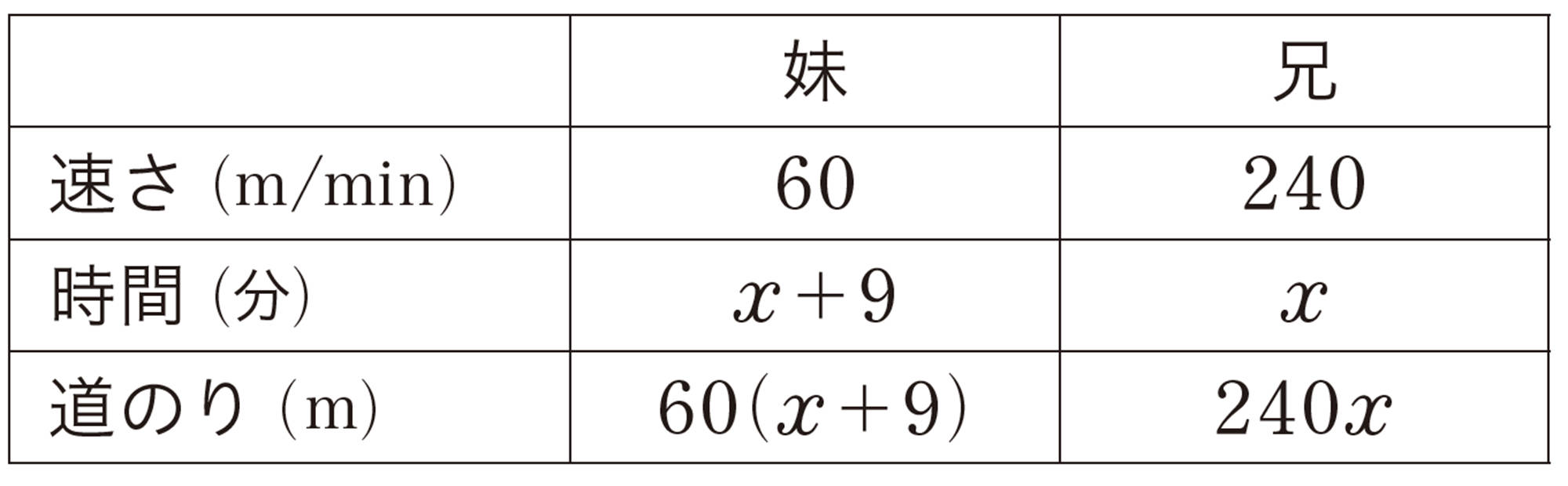
兄が出発してからx分後に妹に追いつくとして，速さ，時間，道のりの関係を次のような表にまとめ，方程式をつくる。
妹は兄が進んだ時間より9分間長く歩いているね。
解答
兄が出発してから [mathjax] \(x\) 分後に妹に追いつくとすると，
[mathjax] \(60( x+9) \) ，[mathjax] \(240x\) のそれぞれに[mathjax] \(x=3\)を代入すると， どちらも720 となる。
720m は1km 以内であるから， 兄が出発してから3 分後に追いつくことは，
問題に適している。
答 3分後
<1年p.117>
問 ５ 前ページの例3で，妹が出発してからの時間を15分後にした場合には，方程式の解をそのまま答えにしてよいですか。また，その理由を説明しなさい。
方程式を使って問題を解くとき，方程式の解がそのまま問題の答えにならない場合がある。したがって，方程式の解がその問題に適しているかどうかを確かめておく必要がある。
問 ６ トラックが高速道路の A 地点を出発し，その1時間後に乗用車が同じ A 地点を出発しました。トラックの速さを時速60km，乗用車の速さを時速100kmとするとき，乗用車が出発してから何時間後にトラックに追いつきますか。
方程式を利用して問題を解くときには，次の手順で考えるとよい。
方程式を利用して問題を解く手順
❶図や表，ことばの式などを使って，数量の関係を見つける。
❷文字を使って方程式をつくる。
❸方程式を解く。
❹方程式の解が問題に適しているかどうかを確かめ，適していれば問題の答えとする。
ふつうは，求める数量をxで表せばいいね。
どんなことがわかったかな
身のまわりの問題は，数量の関係から1次方程式をつくれば，1次方程式を利用して解決することができます。ただし，方程式の解が問題に適しているかどうかを確かめる必要があります。
