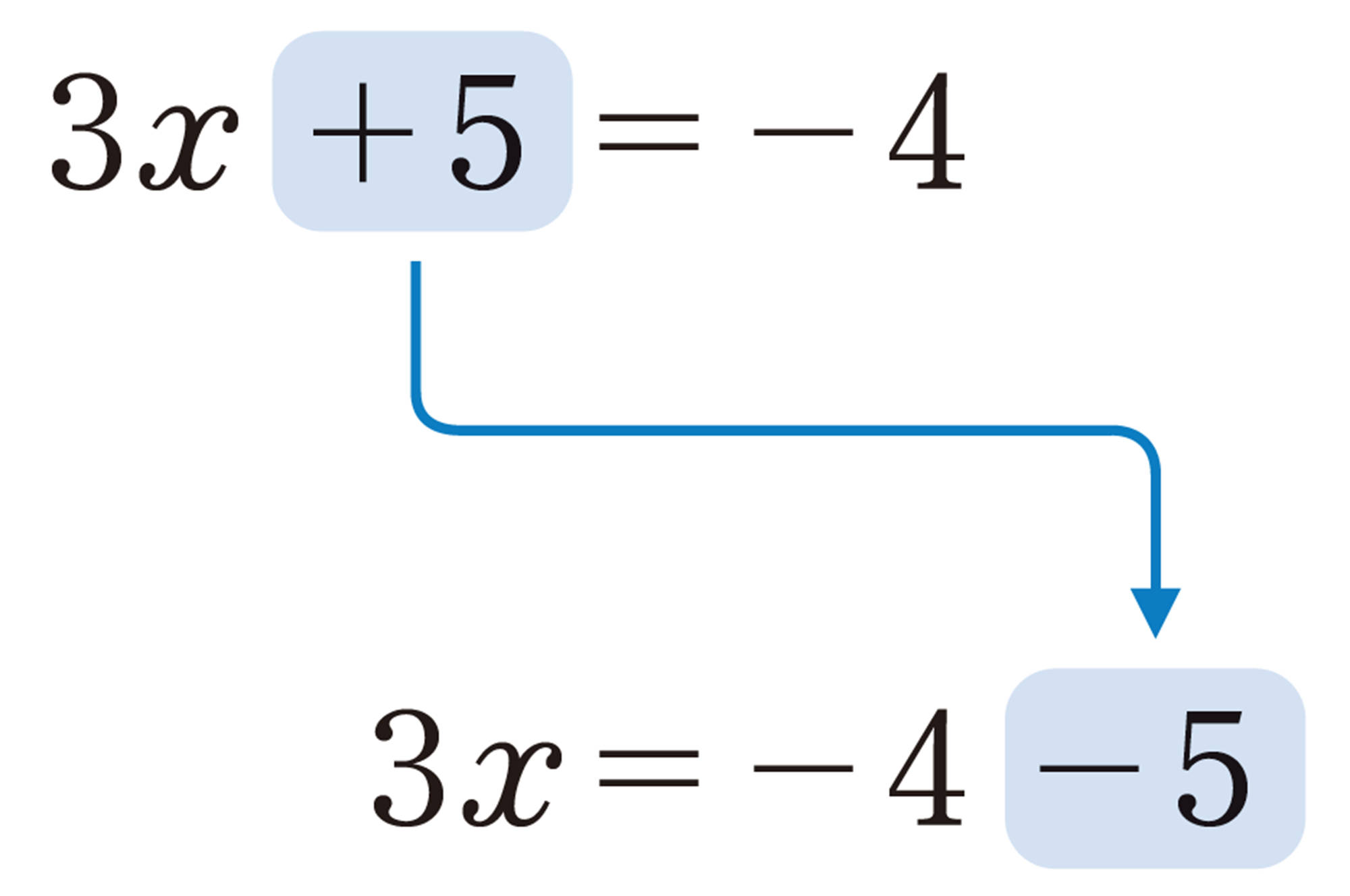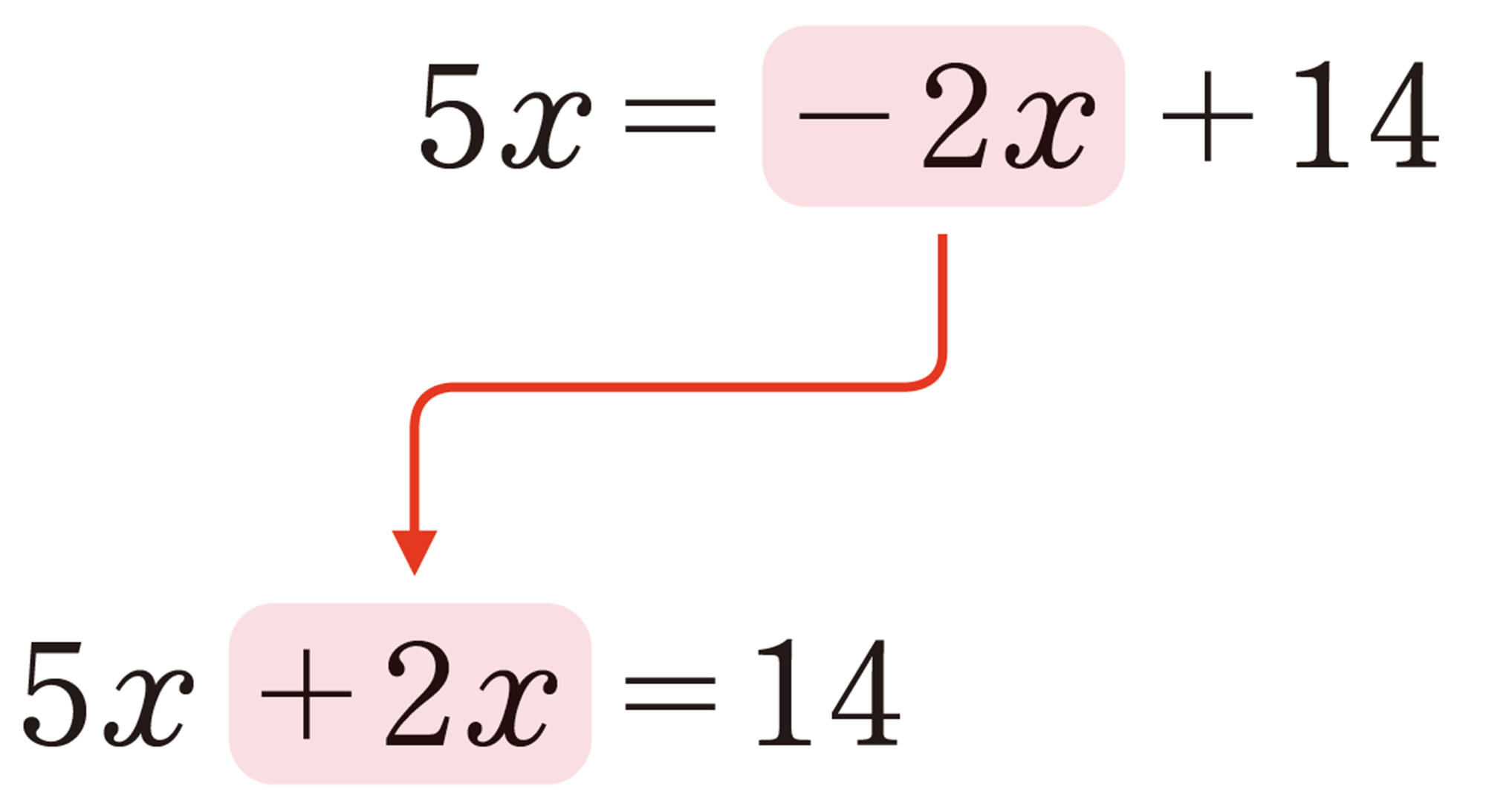<1年p.102>
２ 方程式
Q Question
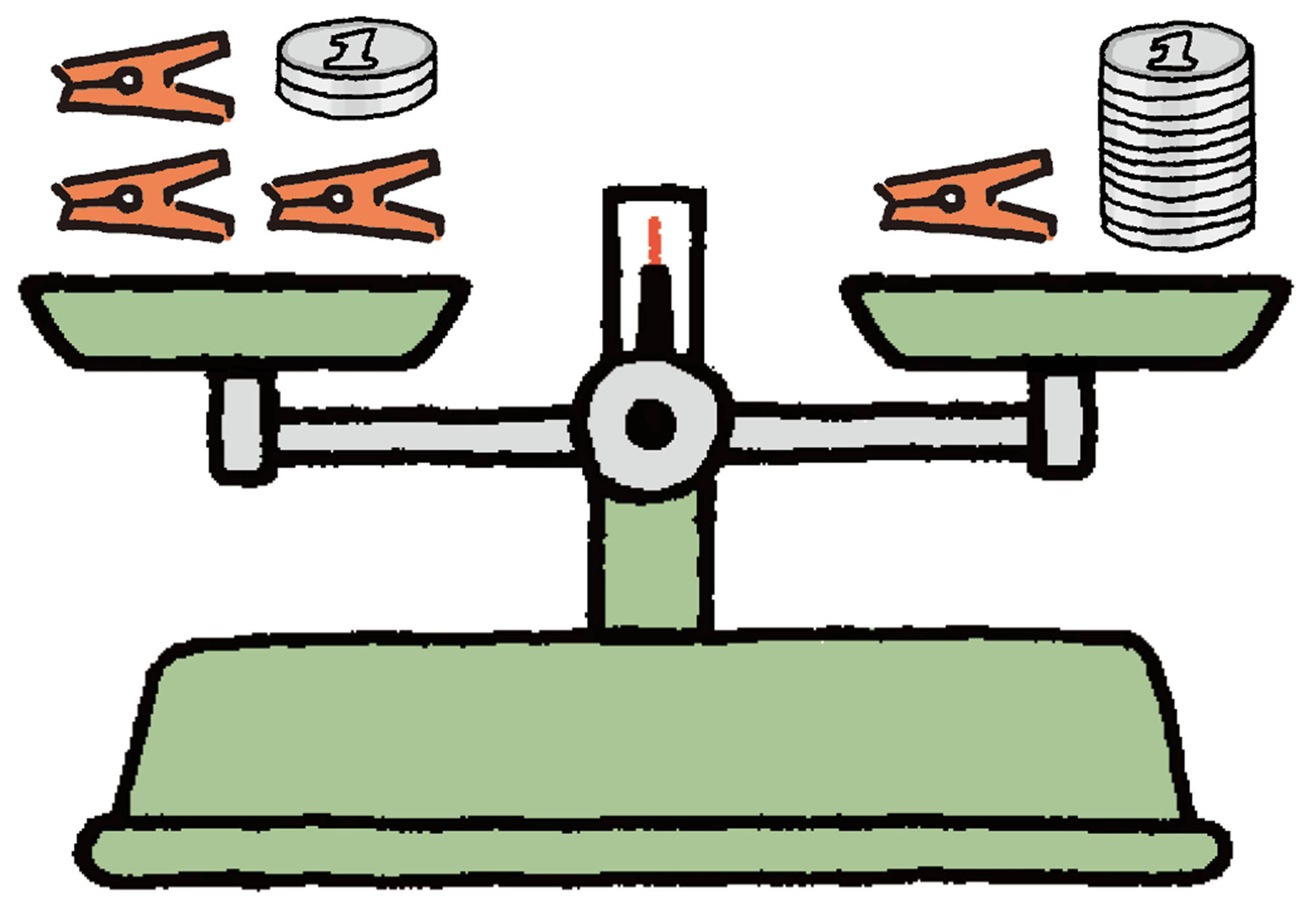
97ページの【１】 ❷の天びんについて，左右の重さの関係を等式で表すと，[mathjax]\(3x+2=x+10\)となります。この式のxの値を求めるには，どうすればよいか考えてみましょう。
わからない数が両辺にあるときは，どうすればいいのかな。
見方・考え方
小学校でわからない数を求めたときと同じように考えられるかな。
目標 ▷ 等式を成り立たせる，文字にあてはまる値の求め方を考えよう。
問 １ 【Q】の等式[mathjax]\(3x+2=x+10\)の両辺のxに1から5までの整数をそれぞれ代入して，等式が成り立つかどうかを調べなさい。また，このことから，クリップ1個の重さは，何gになりますか。
等式[mathjax]\(3x+2=x+10\)のxに，1から順に整数を代入すると，xの値が4のとき，左辺の値と右辺の値が等しくなり，等式が成り立つ。それ以外の値では成り立たない。
このように，xの値によって成り立ったり成り立たなかったりする等式を，xについての方程式 という。
また，方程式を成り立たせるxの値を，方程式の 解 といい，方程式の解を求めることを，方程式を 解く という。
方程式[mathjax]\(3x+2=x+10\)の解は4である。
クリップ1個の重さが4g ということだね。
おしえて！
P.122
不等式にも解はあるのかな？
<1年p.103>
例 １ 方程式[mathjax]\(2x+5=11\)の解は，[mathjax] \(1\)，[mathjax] \(2\)，[mathjax] \(3\)のうちどれですか。
解答
[mathjax] \(2x+5=11\) のxに，[mathjax] \( 1\)，[mathjax] \( 2\)，[mathjax] \( 3\) をそれぞれ代入すると， 左辺は，
[mathjax] \(x=1\) のとき， [mathjax] \(2 \times 1+5=7\)
[mathjax] \(x=2\) のとき， [mathjax] \(2 \times 2+5=9\)
[mathjax] \(x=3\) のとき， [mathjax] \(2 \times 3+5=11\)
以上より，[mathjax] \(x=3\) のとき， 等式が成り立つ。
答 解は3 である
問 ２ 次の方程式の解は，3，4，5のうちどれですか。
⑴ [mathjax] \(2x-3=7\)
⑵ [mathjax] \(x+2=10-x\)
問 ３ 次の㋐～㋓の方程式のうち，解が2であるものはどれですか。また，解が-2であるものはどれですか。
㋐ [mathjax] \(3x+2=8\)
㋑ [mathjax] \(x-5=3\)
㋒ [mathjax] \(-2x=4\)
㋓ [mathjax] \(2x-3=x-1\)
どんなことがわかったかな
方程式の解は，文字にいろいろな数を代入して，方程式が成り立つかどうかで求めることができます。
次の課題へ！
文字に数を代入しないで，方程式を解く方法はあるのかな？
P.104
用語の由来「方程式」 Tea Break
方程式の「方程」ということばは，中国で1世紀頃にまとめられた『九章算術』という数学書の第八巻の表題に出てきます。
『九章算術』では，「算木」と呼ばれる数を表す棒を，「算盤」と呼ばれる位取り表のます目の上に並べ，算木を操作することによって方程式を解いています。
「方程」の語源には，いろいろな説があります。その中の1つの説では，“方”は「左右」，“程”は「大小の比較」を表し，“方程”の意味は，「左右を比べまとめる」ことと考えられています。
<1年p.104>
３ 方程式の解き方
Q Question
97ページの1 ②の天びんでは，
左側の重さは，[mathjax]\((3x+2)\)g ，
右側の重さは，[mathjax]\((x+10)\)g
です。天びんがつり合ったままで，片方がクリップ1個になるようにするには，どんな操作をすればよいでしょうか。
左右から同じものを取っても，天びんはつり合ったままだね。
左右から同じものを取る以外には，どんなことができるかな。
見方・考え方
天びんの操作と式を関連づけて考えられるかな。
目標 ▷ 文字に数を代入せずに，方程式を解く方法を考えよう。
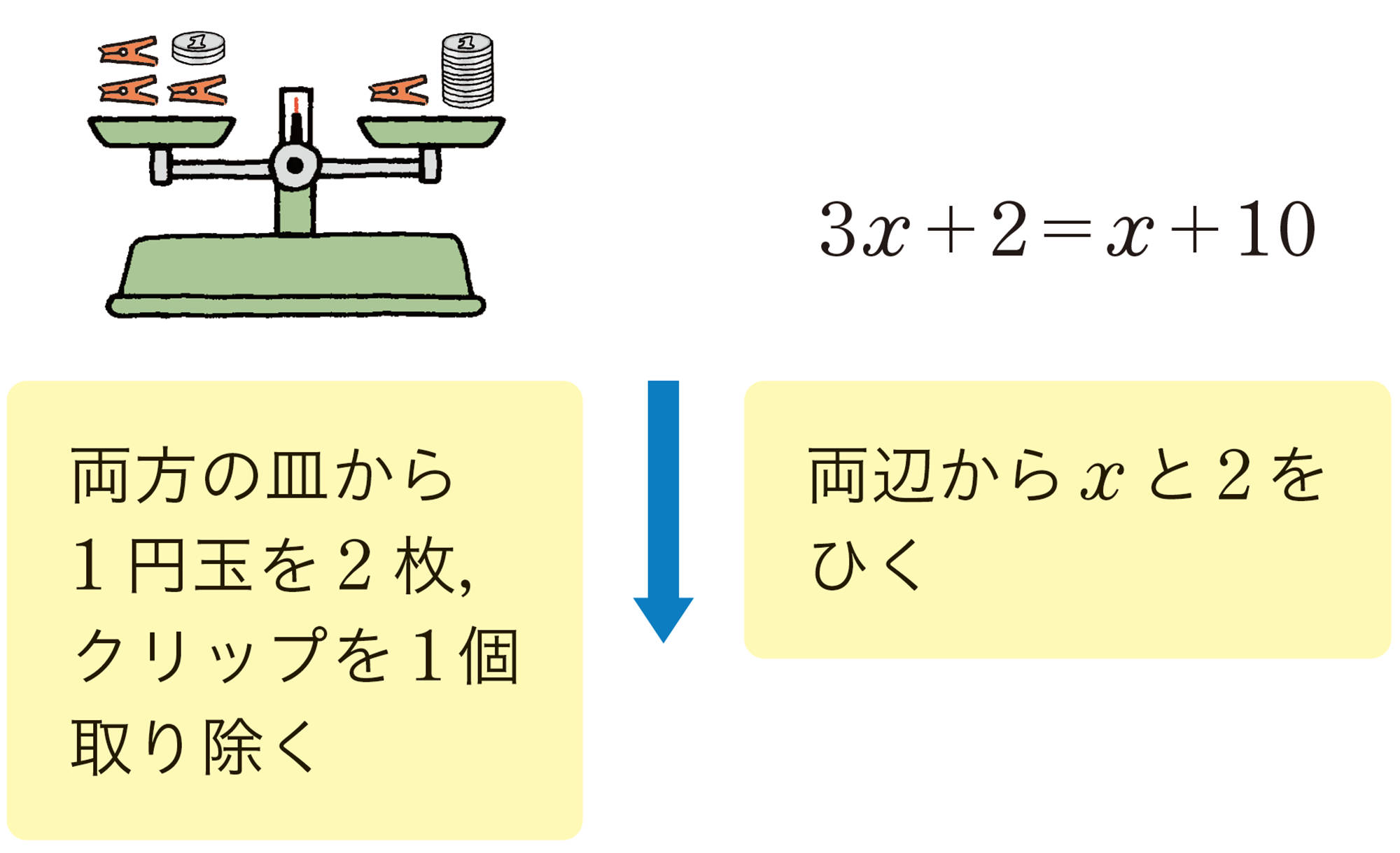
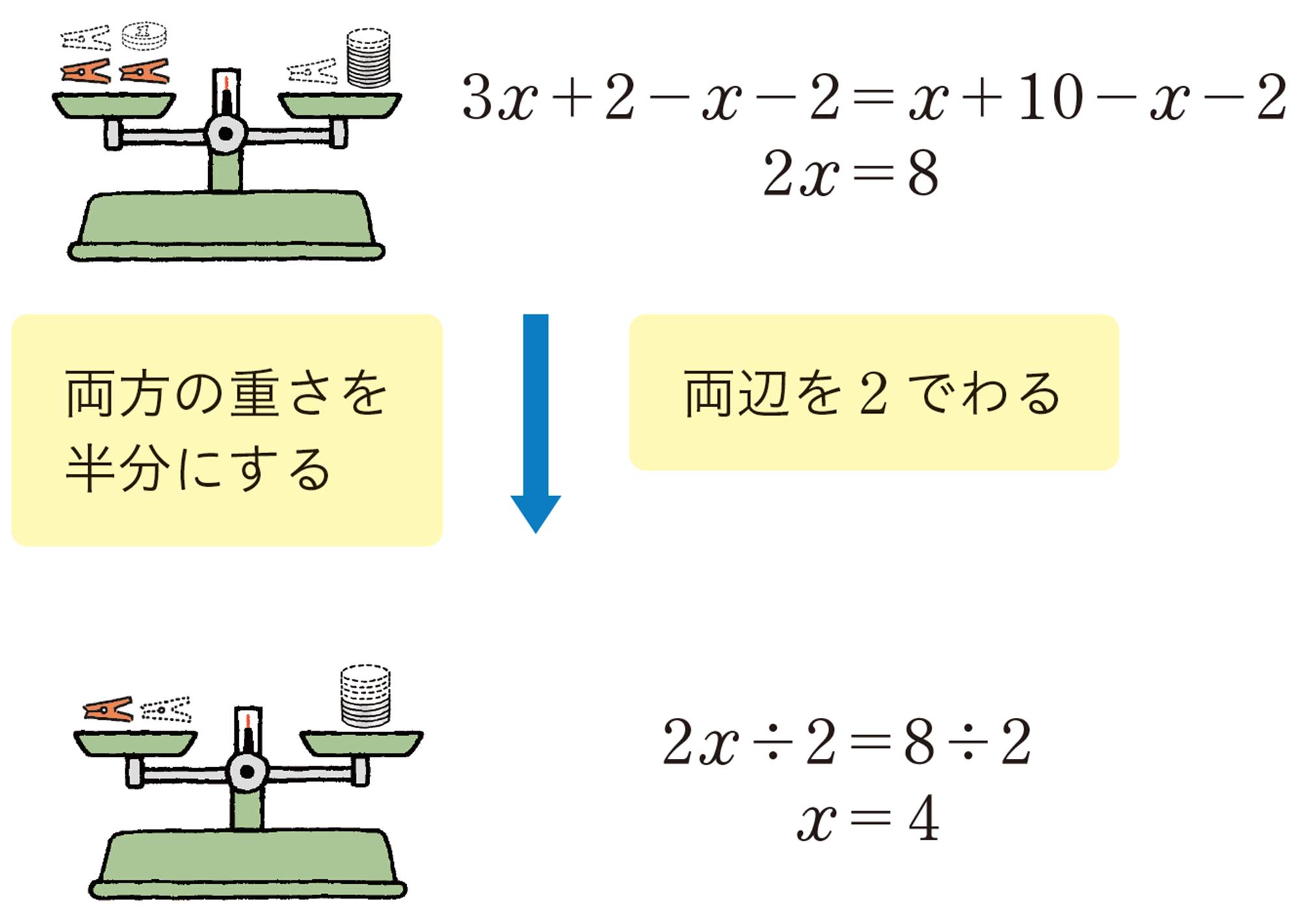
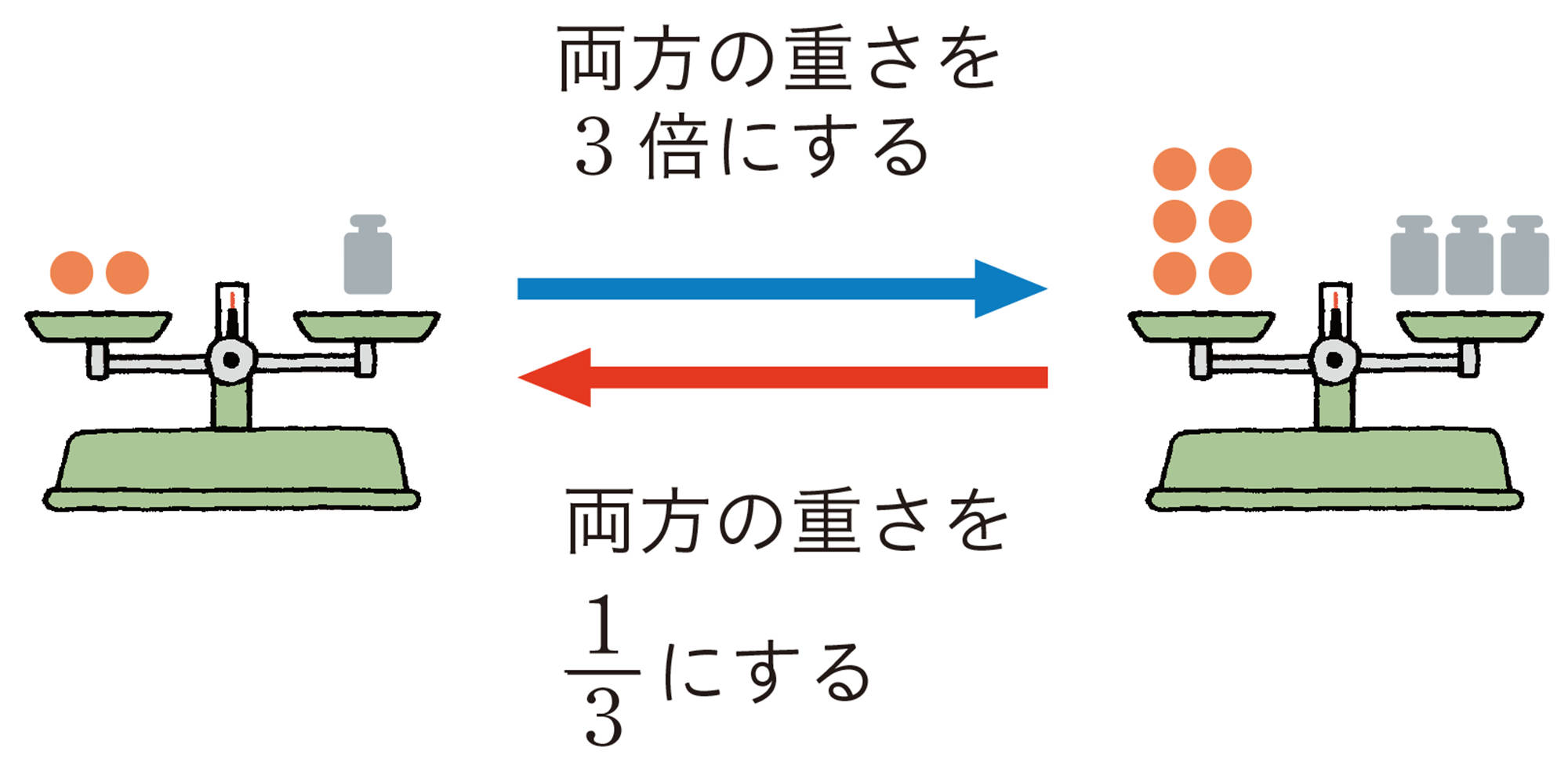
つり合っている天びんでは，両方の皿から同じ重さのものを取り除いたり，両方の重さを半分にしたりしても，天びんはつり合ったままになる。
このことを等式で考えると，右のようになる。
右の図から，クリップ1個の重さが4g であることがわかる。
また，このことから，方程式を「[mathjax]\(x=\textsf{(数)}\)」の形に変形することができれば，解を求めることができることがわかる。
[mathjax]\(3x+2=x+10\)
<1年p.105>
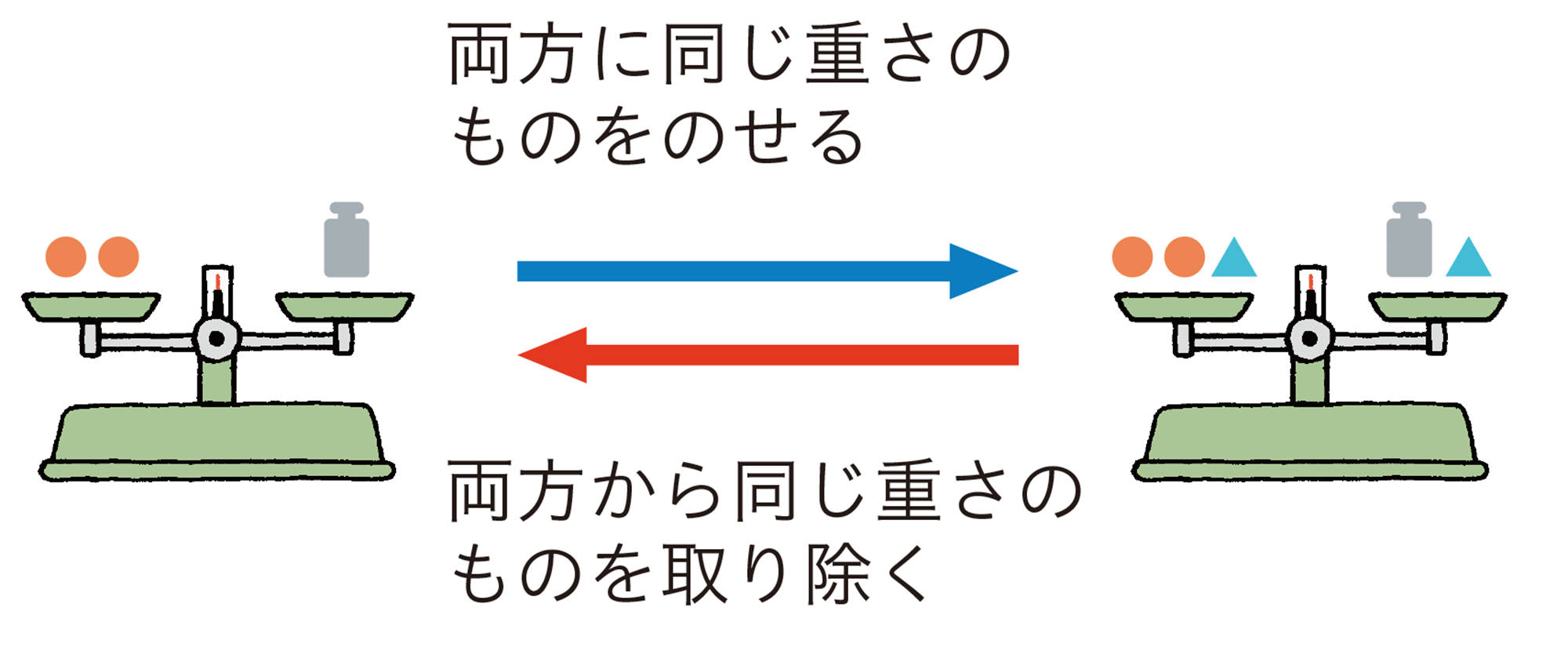
つり合っている天びんに，次のような操作をしても天びんはつり合う。
両方に同じ重さのものをのせる
両方から同じ重さのものを取り除く
両方の重さを 3倍にする
両方の重さを[mathjax]\(\dfrac{1}{3}\)にする
つり合っている天びんと同じように，等式には次のような性質がある。
等式の性質
①等式の両辺に同じ数や式mを加えても，等式は成り立つ。
[mathjax]\(A=B\)ならば，[mathjax]\(A+m=B+m\)
②等式の両辺から同じ数や式mをひいても，等式は成り立つ。
[mathjax]\(A=B\)ならば，[mathjax]\(A-m=B-m\)
③等式の両辺に同じ数mをかけても，等式は成り立つ。
[mathjax]\(A=B\)ならば，[mathjax]\(Am=Bm\)
④等式の両辺を同じ数[mathjax]\(m(m \neq 0)\)でわっても，等式は成り立つ。
[mathjax]\(A=B\)ならば，[mathjax]\(\dfrac{A}{m}=\dfrac{B}{m}\)
注意 [mathjax]\(m \neq 0\)は，mは0でないことを表している。
また，等式の両辺を入れかえても，その等式は成り立つ。
[mathjax]\(A=B \ \text{ならば}，B=A\)
等式の性質を使った方程式の解き方
例 １
⑴ [mathjax]\(x+6=-2\)
両辺から6をひくと，
⑵ [mathjax]\(x-3=4\)
両辺に3を加えると，
例1⑴で導いた等式[mathjax]\(x=-8\)は，方程式[mathjax]\(x+6=-2\)の解が[mathjax] \(-8\)であることを示している。
<1年p.106>
問 １ 前ページの例1⑴で，[mathjax]\(x=-8\)をもとの方程式に代入して，[mathjax] \(-8\)が解であることを確かめなさい。また⑵ で，[mathjax]\(x=7\)をもとの方程式に代入して，7が解であることを確かめなさい。
問 ２ 次の方程式を，等式の性質を使って解きなさい。
⑴ [mathjax]\(x+4=10\)
⑵ [mathjax]\(x+7=-2\)
⑶ [mathjax]\(x-6=3\)
⑷ [mathjax]\(x-2=-8\)
例 ２
⑴ [mathjax]\(6x=24\)
両辺を6でわると，
⑵[mathjax]\(\dfrac{1}{2}x=-3\)
両辺に2をかけると，
問 ３ 次の方程式を，等式の性質を使って解きなさい。
⑴ [mathjax]\(4x=32\)
⑵ [mathjax]\(-3x=18\)
⑶ [mathjax]\(-x=-10\)
⑷ [mathjax]\(8x=4\)
⑸ [mathjax]\(\dfrac{1}{3}x=5\)
⑹ [mathjax]\(\dfrac{1}{5}x=-6\)
⑺ [mathjax]\(-\dfrac{1}{2}x=-8\)
⑻ [mathjax]\(\dfrac{x}{7}=-1\)
やってみよう
計算力を高めよう4-1
P.112
問 ４ これまでの学習をもとに，解が8になる方程式をつくりなさい。
等式の性質の見方 Tea Break
等式の性質②で，等式[mathjax]\(A=B\)の両辺から【mをひくこと】は，次のように，等式の両辺に【-mを加えること】とみることができます。
[mathjax]\(A-m=B-m\) → [mathjax]\(A+(-m)=B+(-m)\)
同じように，等式の性質❹で，等式[mathjax]\(A=B\)の両辺を【[mathjax]\(m(m \neq 0)\)でわること】は，次のように，等式の両辺に【[mathjax]\(\dfrac{1}{m}\)をかけること】とみることができます。
[mathjax]\(\dfrac{A}{m}=\dfrac{B}{m}\) → [mathjax]\(A \times \dfrac{1}{m}=B \times \dfrac{1}{m}\)
このような見方をすれば，等式の性質❶と❷，❸と❹は，それぞれ1つにまとめることができます。
<1年p.107>
Q Question
次の㋐ ，㋑は，等式の性質を使って方程式を解いたものです。それぞれ，式がどのように変わっていくか調べてみましょう。
見方・考え方
式変形の根拠を説明できるかな。
㋐
㋑
㋐と㋑ では，どこが似ているのかな。
等式の性質を使うと，文字に数を代入するより，簡単に解を求められたね。
もっと，効率よく解を求める方法はあるかな。
①では左辺に数の項[mathjax] \(-9\)があったが，両辺に9を加えたために，②では左辺から[mathjax] \(-9\)が消えている。
その代わりに， ②では右辺に数の項[mathjax] \(+9\)が現れている。
２ 【Q】㋐ ，㋑で， ①の式からすぐに②の式を導くにはどうすればよいでしょうか。 【1】で調べたことをもとに，説明しましょう。
㋐
㋑
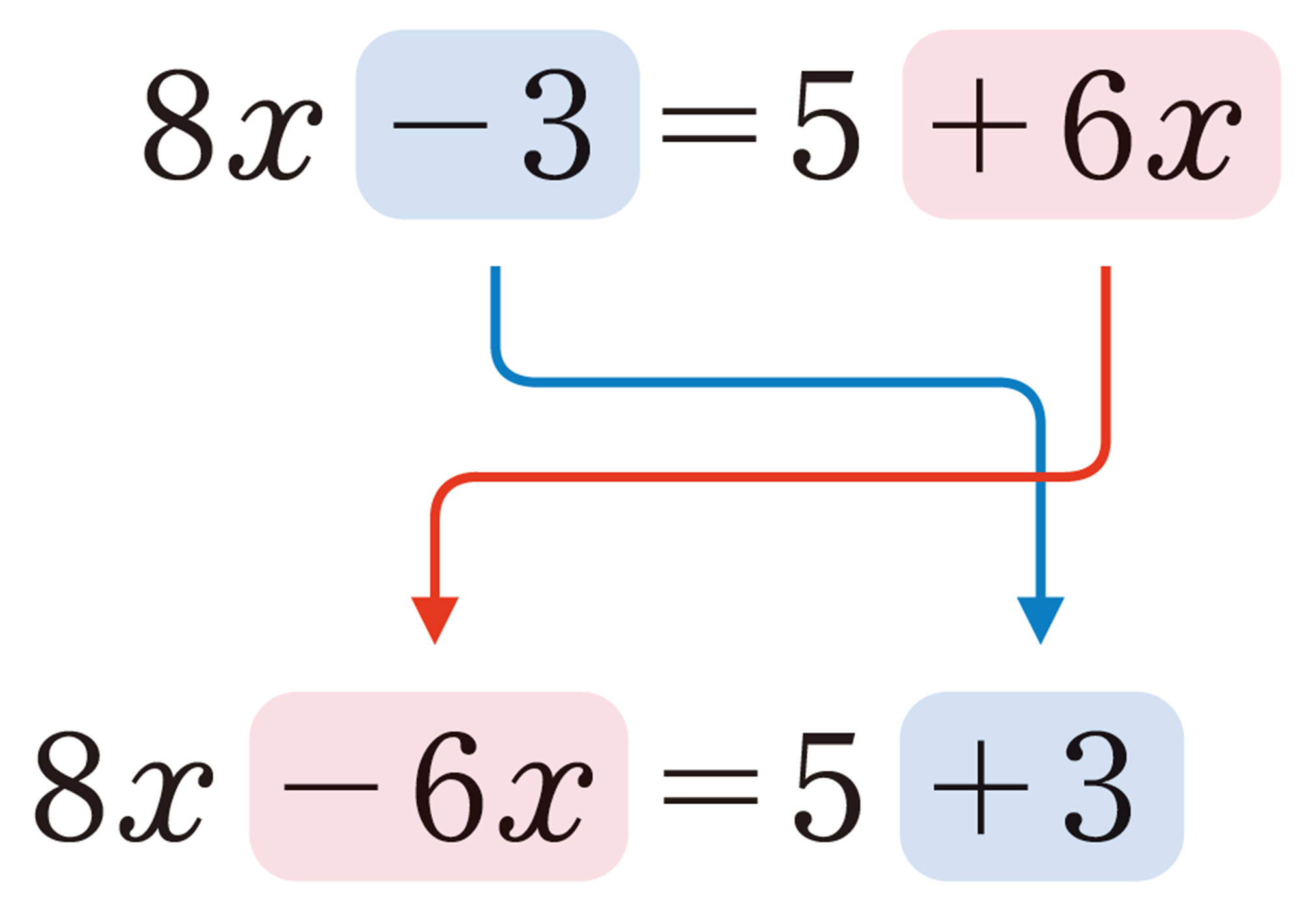
等式では，一方の辺にある項を，符号を変えて他方の辺に移すことができる。このことを移項という。
㋐
移項
㋑
移項
<1年p.108>
移項を使った方程式の解き方
例 ３
⑴ [mathjax]\(3x+5 =-4\)
5を移項すると，
⑵ [mathjax]\(5x =-2x+14\)
[mathjax] \(-2x\)を移項すると，
問 ５ 例3で，解が正しいことを，解をもとの方程式に代入して確かめなさい。
方程式を解くには，文字の項を左辺に，数の項を右辺に移項して，[mathjax]\(ax=b\)の形に変形する。次に，両辺をxの係数aでわる。
問 ６ 次の方程式を解きなさい。
⑴ [mathjax]\(2x+1=9\)
⑵ [mathjax]\(4x-5=-13\)
⑶ [mathjax]\(3x=-2x-15\)
⑷ [mathjax]\(2x=3x-8\)
例 ４ 方程式[mathjax]\(8x-3=5+6x\)を解きなさい。
解答
[mathjax] \(8x-3=5+6x\)
[mathjax] \(-3\)，[mathjax] \( 6x\) を移項すると
答 [mathjax] \(x=4\)
見直したときわかりやすいように，「[mathjax]\(=\)」をそろえて書いておこう。
問 ７ 次の方程式を解きなさい。
⑴ [mathjax]\(6x-12=3x\)
⑵ [mathjax]\(7x-3=5x+7\)
⑶ [mathjax]\(5x+15=-2x+1\)
⑷ [mathjax]\(3+7x=4x-6\)
⑸ [mathjax]\(8+2x=3x-1\)
⑹ [mathjax]\(-3x+2=x+4\)
やってみよう
計算力を高めよう4-2
P.112
<1年p.109>
かっこをふくむ方程式
例 ５ 方程式[mathjax] \(5x-2(x-3)=3\)を解きなさい。
考え方 分配法則を使って，かっこをはずしてから解く。
解答
6 を移項すると，
答 [mathjax] \(x=-1\)
分配法則で負の数をかけるときは，符号に注意しよう。
問 ８ 次の方程式を解きなさい。
⑴ [mathjax] \(2(x-5)+1=7\)
⑵ [mathjax] \(4x-7(x+2)=-5\)
⑶ [mathjax] \(-2(x+3)=5x+8\)
⑷ [mathjax] \(3(x-8)=-6(x+4)\)
やってみよう
計算力を高めよう4-3
P.112
小数や分数をふくむ方程式
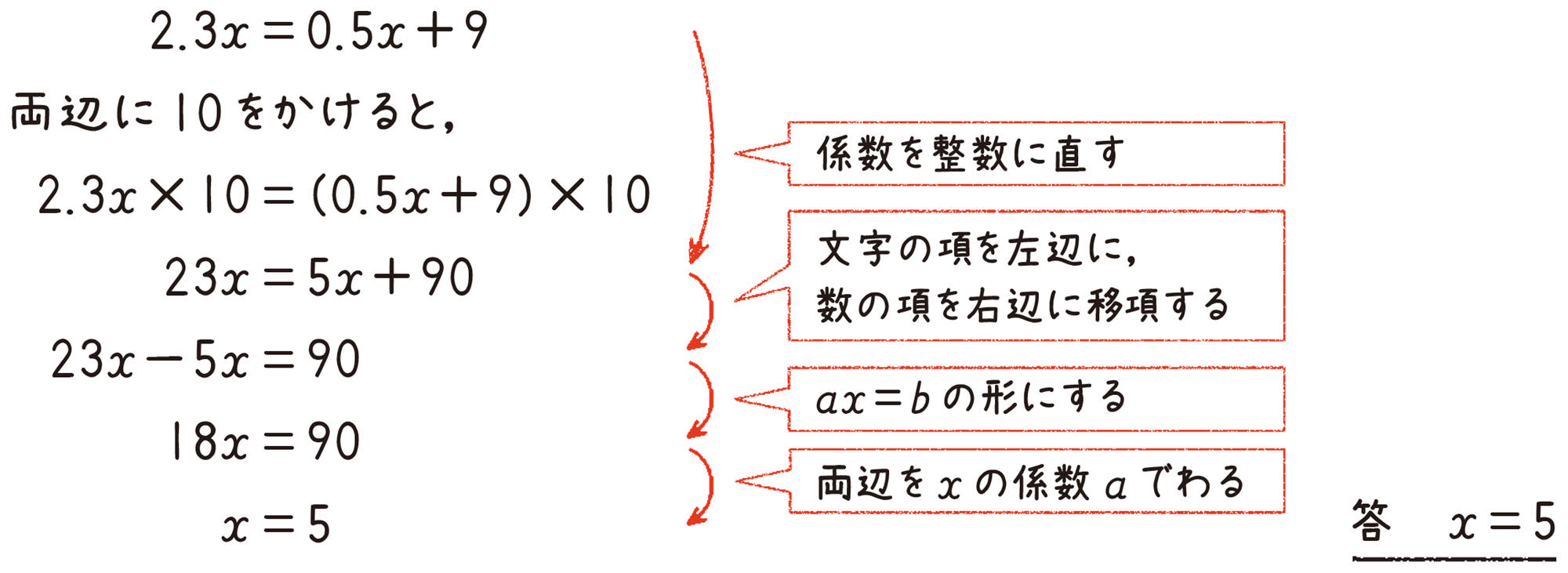
例 ６ 方程式[mathjax] \(2.3x=0.5x+9\)を解きなさい。
考え方 計算しやすくするために，両辺に10をかけて，係数を整数に直す。
解答
[mathjax] \(2.3x=0.5x+9\)
両辺に10 をかけると，
答 [mathjax] \(x=5\)
係数を整数に直す
文字の項を左辺に，数の項を右辺に移項する
[mathjax]\(ax=b\)の形にする
両辺をxの係数aでわる
係数に小数をふくむ方程式では，両辺に[mathjax] \(10\)，[mathjax] \(100\)などをかけて，係数を整数に直してから解くとよい。
問 ９ 次の方程式を解きなさい。
⑴ [mathjax] \(0.4x+2=0.3x\)
⑵ [mathjax] \(0.25x=0.2x-0.1\)
やってみよう
計算力を高めよう4-4
P.112
<1年p.110>
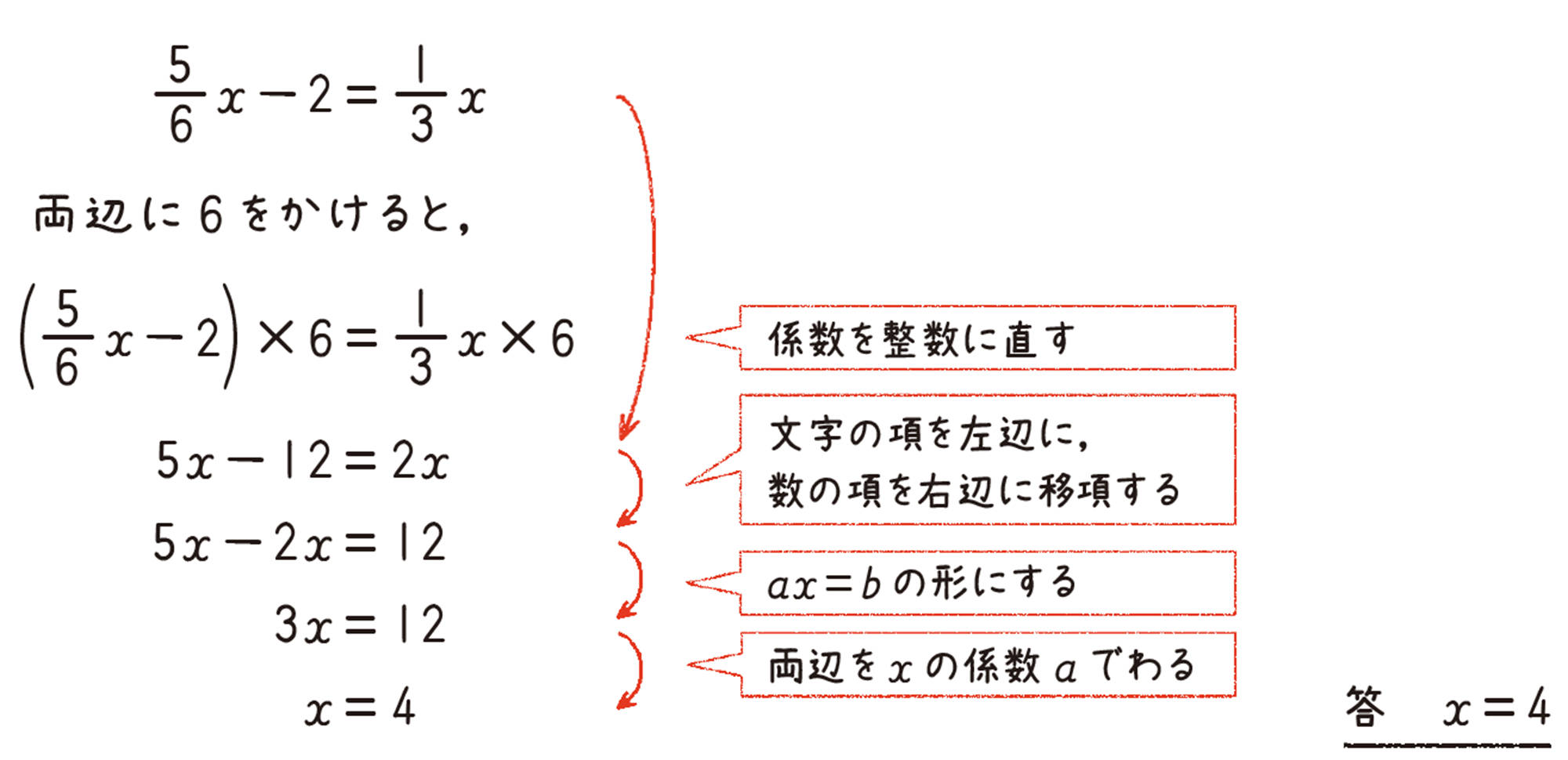
例 ７ 方程式[mathjax] \(\dfrac{5}{6}x-2=\dfrac{1}{3}x\)を解きなさい。
考え方 計算しやすくするために，両辺に6と3の公倍数をかけて，係数を整数に直す。
解答
[mathjax] \(\dfrac{5}{6}x-2=\dfrac{1}{3}x\)
両辺に6 をかけると，
答 [mathjax] \(x=4\)
係数を整数に直す
文字の項を左辺に，数の項を右辺に移項する
[mathjax]\(ax=b\)の形にする
両辺をxの係数aでわる
係数に分数をふくむ方程式では，両辺に分母の公倍数をかけて，係数を整数に直してから解くとよい。
このようにすることを， 分母をはらう という。
最小公倍数をかけると，簡単な数になるね。
問 10 次の方程式を解きなさい。
⑴ [mathjax]\(\dfrac{1}{2}x=\dfrac{2}{5}x-1\)
⑵ [mathjax]\(\dfrac{2}{3}x-\dfrac{1}{2}=\dfrac{1}{6}x+2\)
⑶ [mathjax]\(\dfrac{x-3}{2}=-4\)
⑷ [mathjax]\(\dfrac{x+2}{6} = \dfrac{x-3}{4}\)
やってみよう
計算力を高めよう4-5
P.112
方程式を解く手順
❶係数に小数や分数があるときは，整数に直すとよい。かっこがあれば，かっこをはずす。
❷文字の項を左辺に，数の項を右辺に移項する。
❸両辺をそれぞれ計算し，[mathjax]\(ax=b \ (a \neq 0)\)の形にする。
❹両辺をxの係数aでわる。
<1年p.111>
これまで解いてきたxについての方程式は，すべての項を左辺に移項して整理すると，
[mathjax]\(ax+b=0 \quad (a \neq 0)\)
のように， 左辺がxについての1次式になる。このような方程式を， 1次方程式 という。
どんなことがわかったかな
等式の性質や移項を使えば，1次方程式を解くことができます。
次の課題へ！
1次方程式は，どんなところで使えるのかな？
P.113，118
確かめよう 1節 方程式
１ 次の数量の関係を，等式や不等式で表しなさい。
⑴ 1個a kg の荷物7個の重さは，40kg より重くなる。
⑵ 120円のカレーパンx個と200円の牛乳を買ったときの代金は，160円のコロッケパンy個を買ったときの代金と等しい。
⑶ 時速4 km でx時間歩いたときの道のりは，20 km 以下である。
２ 次の㋐〜㋒の方程式のうち，解が3であるものはどれですか。
㋐ [mathjax]\(x-7=10\)
㋑ [mathjax]\(4x=12\)
㋒ [mathjax]\(3x+1=9\)
３ 次の方程式を，等式の性質を使って解きなさい。
⑴ [mathjax]\(x-4=-1\)
⑵ [mathjax]\(x+5=-2\)
⑶ [mathjax]\(7x=-42\)
⑷ [mathjax]\(\dfrac{1}{3}x=9\)
４ 次の方程式を解きなさい。
⑴ [mathjax]\(2x-3=5\)
⑵ [mathjax]\(3x=5x-12\)
⑶ [mathjax]\(6x-17=-3x+10\)
⑷ [mathjax]\(4x+12=7-x\)
⑸ [mathjax]\(5-4x=2x-1\)
⑹ [mathjax]\(3(x-5)=-6\)
<1年p.112>
計算力を高めよう ４
家庭学習や計算練習で利用しましょう。
方程式 解答P.303〜304
次の方程式を解きなさい。
１ 等式の性質
⑴ [mathjax]\(x+5=9\)
⑵ [mathjax]\(x-8=3\)
⑶ [mathjax]\(x+1=-7\)
⑷ [mathjax]\(x-6=-5\)
⑸ [mathjax]\(8x=48\)
⑹ [mathjax]\(-2x=18\)
⑺ [mathjax]\(-9x=-63\)
⑻ [mathjax]\(12x=-20\)
⑼ [mathjax]\(\dfrac{1}{4}x=5\)
⑽ [mathjax]\(\dfrac{x}{3}=-2\)
２ 係数が整数の方程式
⑴ [mathjax]\(4x-5=7\)
⑵ [mathjax]\(3x+7=4\)
⑶ [mathjax]\(-x+8=2\)
⑷ [mathjax]\(5-7x=-16\)
⑸ [mathjax]\(4x=0\)
⑹ [mathjax]\(10x=8x-6\)
⑺ [mathjax]\(-2x=10+3x\)
⑻ [mathjax]\(5x+21=2x\)
⑼ [mathjax]\(6x-4=x\)
⑽ [mathjax]\(3x-5=x+7\)
⑾ [mathjax]\(8x-2=5x+1\)
⑿ [mathjax]\(7x-2=4x-16\)
⒀ [mathjax]\(x+5=4x+7\)
⒁ [mathjax]\(5-4x=1-2x\)
⒂ [mathjax]\(2-5x=3x-10\)
３ かっこをふくむ方程式
⑴ [mathjax]\(3(x+6)=x+2\)
⑵ [mathjax]\(6x-(2x-9)=11\)
⑶ [mathjax]\(9x-2(3x+5)=2\)
⑷ [mathjax]\(7(x-2)=4(x-5)\)
４ 係数に小数をふくむ方程式
⑴ [mathjax]\(0.4x+0.2=-1.8\)
⑵ [mathjax]\(0.7x-1=0.3x+2\)
⑶ [mathjax]\(0.13x=0.07x-0.3\)
⑷ [mathjax]\(0.75x-2=0.5x\)
５ 係数に分数をふくむ方程式
⑴ [mathjax]\(3x-1=\dfrac{x}{2}\)
⑵ [mathjax]\(\dfrac{1}{2}x-\dfrac{1}{3} = -\dfrac{1}{3}x+3\)
⑶ [mathjax]\(\dfrac{x-8}{3}=-5\)
⑷ [mathjax]\(\dfrac{x+5}{6}=\dfrac{3x+1}{4}\)
