<1年p.89>
計算力を高めよう 3
家庭学習や計算練習で利用しましょう。
式の計算 解答P.303
１ 1次式
⑴ [mathjax]\(4a+3a\)
⑵ [mathjax]\(8a-6a\)
⑶ [mathjax]\(-2x-4x\)
⑷ [mathjax]\(9a-10a\)
⑸ [mathjax]\(-2x+7x\)
⑹ [mathjax]\(4a+6+a+3\)
⑺ [mathjax]\(-5x+10+3x-9\)
⑻ [mathjax]\(7-8a-a+6\)
⑼ [mathjax]\(2.7x-1.4x\)
⑽ [mathjax]\(\dfrac{2}{3}y+\dfrac{5}{6}y\)
２ 1次式の加法・減法
⑴ [mathjax]\((6x+2)+(2x-9)\)
⑵ [mathjax]\((5-6x)+(9x-7)\)
⑶ [mathjax]\(\require{physics} \left(\dfrac{4}{9}x-\dfrac{5}{3}\right)+\require{physics} \left(\dfrac{5}{9}x+\dfrac{4}{3}\right)\)
⑷ [mathjax]\((7x+4)-(5x-1)\)
⑸ [mathjax]\((-2y+8)-(3y+6)\)
⑹ [mathjax]\((14-a)-(-9-a)\)
⑺ [mathjax]\(\require{physics}\left(\dfrac{1}{4}y+6\right)-\require{physics}\left(-\dfrac{1}{2}y-3\right)\)
３ 1次式と数の乗法・除法
⑴ [mathjax]\(9a \times 3\)
⑵ [mathjax]\((-5) \times 8x\)
⑶ [mathjax]\(-0.6y \times 4\)
⑷ [mathjax]\(12 \times \dfrac{4}{3}a\)
⑸ [mathjax]\(15y \div 5\)
⑹ [mathjax]\(21a \div (-3)\)
⑺ [mathjax]\((-8x) \div 24\)
⑻ [mathjax]\(30a \div \dfrac{5}{6}\)
⑼ [mathjax]\(-3(a+7)\)
⑽ [mathjax]\((6x-5)\times 4\)
⑾ [mathjax]\(\dfrac{1}{2}(8a-6)\)
⑿ [mathjax]\(\dfrac{12x-5}{4} \times 8\)
⒀ [mathjax]\((10x-35)\div 5\)
⒁ [mathjax]\((-6a+9)\div (-3)\)
⒂ [mathjax]\((4x-5)\div 2\)
⒃ [mathjax]\((12x+4)\div \dfrac{2}{3}\)
４ いろいろな計算
⑴ [mathjax]\(4x+5(2x-7)\)
⑵ [mathjax]\(7(2a-1)+6(-3a+2)\)
⑶ [mathjax]\(-(4a+7)+3(a+5)\)
⑷ [mathjax]\(9x-2(x-8)\)
⑸ [mathjax]\(8(y-1)-(7y+2)\)
⑹ [mathjax]\(-5(x-1)-4(2x+1)\)
⑺ [mathjax]\(6(2a+4)-8(3-a)\)
⑻ [mathjax]\(\dfrac{1}{4}(x-8)+\dfrac{1}{2}(x-4)\)
⑼ [mathjax]\(\dfrac{1}{9}(3x+7)-\dfrac{1}{3}(x+2)\)
<1年p.90>
2章 「文字式」を学んで
できるようになったこと 身のまわりの課題へ ▷P.[mathjax] \(93\),[mathjax] \(94\),[mathjax] \(286\)
文字を使って数量の関係や求めた結果を表したり，文字を使って表された数量の関係を読み取ったりすることができる。
1次式の計算ができる。
身のまわりや数学の中から見つけた問題を考えるとき，文字式を解決に利用することができる。
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
数学へのいざない 和算における文字を使った式
江戸時代， 日本には 「和算」 という日本独自の数学がありました。鎖国中の日本は，ヨーロッパ諸国と切り離された状況の中，独自の発展をし，世界でも最高レベルの数学を行っていました。その和算を発展させた和算家に， 関孝和（1640頃〜1708）がいます。ニュートンやライプニッツとほぼ同時期に活躍した人です。
関孝和は，和算が独自の発展をするにあたって，重要な役割を果たしました。1674年に『発微算法』を著し，傍書法と呼ばれる記号法を発明して，和算が高等数学として発展するための基礎をつくりました。
傍書法とは，文字を使って式を表す方法のことです。現在では，数字はアラビア数字，文字は英文字を使って表していますが，傍書法では，数字は算木，文字は甲，乙，丙などの文字を使って表していました。このことにより，式を簡単に表すことができるようになり，筆算で計算できるようになりました。
彼は，ほかにもさまざまな業績を残しています。関孝和について，いろいろ調べてみましょう。
関連 P.292
<1年p.91>
２章のまとめの問題 解答 P.303 基本
⑴ [mathjax]\(x \times x \times 8\)
⑵ [mathjax]\(7 \div x\)
⑶ [mathjax]\(5 \times a+1 \times b\)
⑷ [mathjax]\((x-1) \div 2\)
２ 次の数量を，文字式で表しなさい。
⑴ 1個a円の品物7個と1個b円の品物3個を買ったときの代金の合計
⑵ x Lの水があるとき，その20 ％の水の量
⑶ 10 kmの道のりを，時速3 kmでx時間歩いたときの残りの道のり
⑷ 長さa mのテープを，b本に等しく分けたときの1本分の長さ
３ [mathjax]\(x=-9\)，[mathjax]\(y=2\)のとき，次の式の値を求めなさい。
⑴ [mathjax]\(2x+8\)
⑵ [mathjax]\(4x²\)
⑶ [mathjax]\(3x+5y\)
⑷ [mathjax]\(6y-x\)
４ 次の計算をしなさい。
⑴ [mathjax]\(-5x+7x\)
⑵ [mathjax]\(x+9-4x-1\)
⑶ [mathjax]\(a- \dfrac{2}{5}a\)
⑷ [mathjax]\((-3a+7)+(2a-4)\)
⑸ [mathjax]\((x-1)-(3x-4)\)
⑹ [mathjax]\(7a \times (-8)\)
⑺ [mathjax]\(3 \times 0.2x\)
⑻ [mathjax]\((-8x) \div \dfrac{4}{3}\)
⑼ [mathjax]\((-2x+8)\times \dfrac{1}{2}\)
⑽ [mathjax]\((-8x+20)\div (-4)\)
⑾ [mathjax]\(3a-2(a+1)\)
⑿ [mathjax]\(4(4x-3)+2(5-6x)\)
５ 右のような図形について，次の式はどんな数量を表していますか。
⑴ [mathjax]\(ab-cd\)
⑵ [mathjax]\(2(a+b)\)
<1年p.92>
２章のまとめの問題 応用
１ 次の計算をしなさい。
⑴ [mathjax]\(0.5x-1.8-1.3x+2.4\)
⑵ [mathjax]\(\require{physics}\left(\dfrac{2}{3}x-3\right) + \require{physics}\left(\dfrac{x}{2}+\dfrac{3}{4}\right)\)
⑶ [mathjax]\(-\dfrac{4}{3} \require{physics}\left(6x-\dfrac{3}{8}\right)\)
⑷ [mathjax]\(\dfrac{1}{4}(8+x)-\dfrac{5}{8}(2x-16)\)
２ [mathjax]\(x=-6\)，[mathjax]\(y=9\)のとき，次の式の値を求めなさい。
⑴ [mathjax]\(xy+y²\)
⑵ [mathjax]\(\dfrac{x²}{9}-\require{physics}\left(-\dfrac{2}{3}y\right)\)
３ 次のように， 5 を最初の数として，数が規則正しく並んでいます。
[mathjax] \(5\)，[mathjax] \(8\)，[mathjax] \(11\)，[mathjax] \(14\)，[mathjax] \(17\)，[mathjax] \(20\)，[mathjax] \(23\)，…
陸さんは，a番目の数を，[mathjax] \(3a+2\)という式で表しました。次の問いに答えなさい。
⑴ この式は正しいですか。
⑵ 30番目の数を求めなさい。
４ 右の図のように，碁石を並べて正方形をつくります。1辺に並べる碁石の個数をx個として碁石の総数を求めるとき，次の問いに答えなさい。
⑴ 真央さんは，右の図のように正方形を 4つの部分に分けて碁石の総数を求めました。真央さんの考え方を表す式を書きなさい。
⑵ 真央さんとは別の考え方で碁石の総数を求め，それを右の図に示しなさい。また，その考え方を表す式を書きなさい。
<1年p.93>
活用
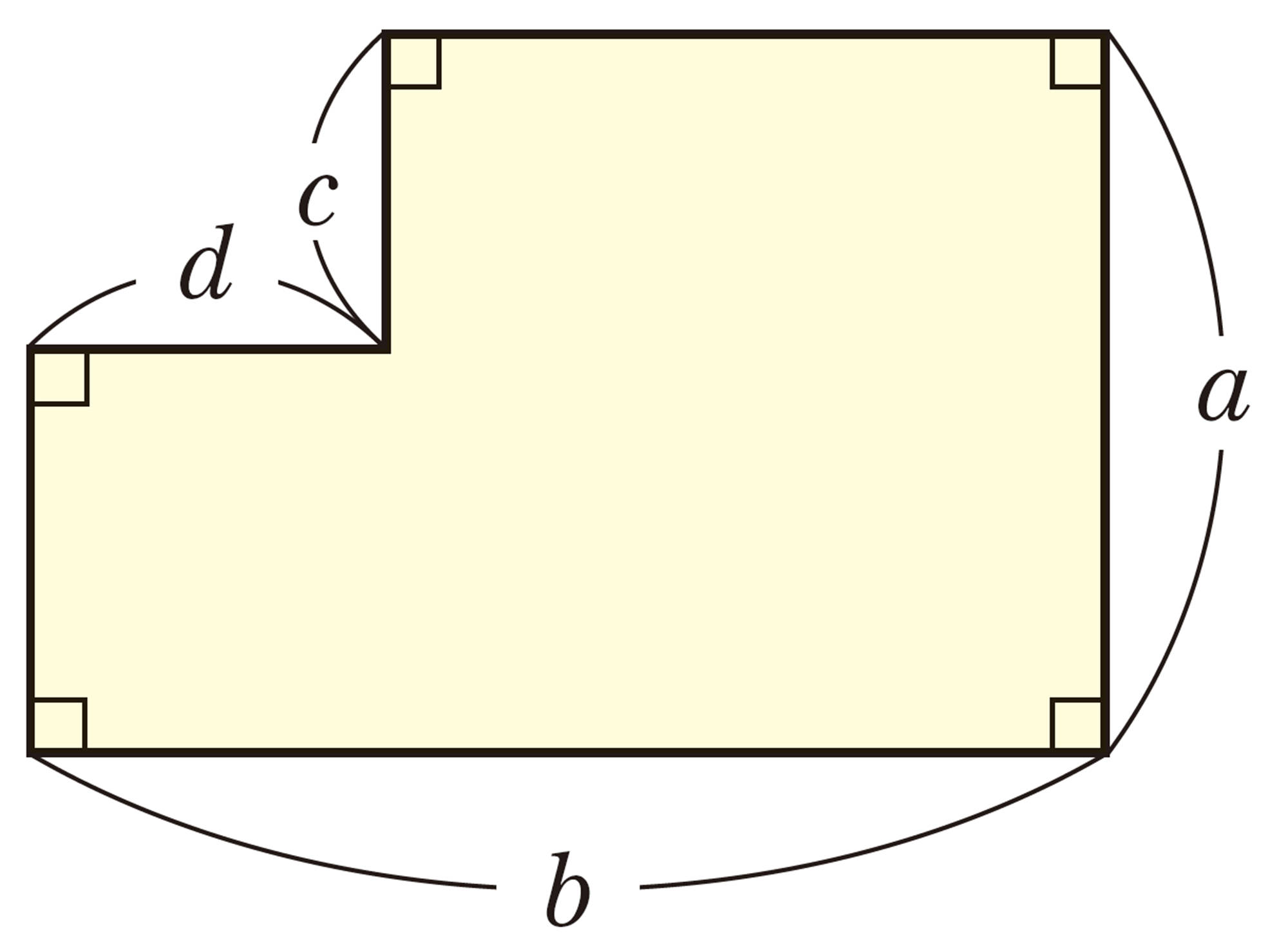
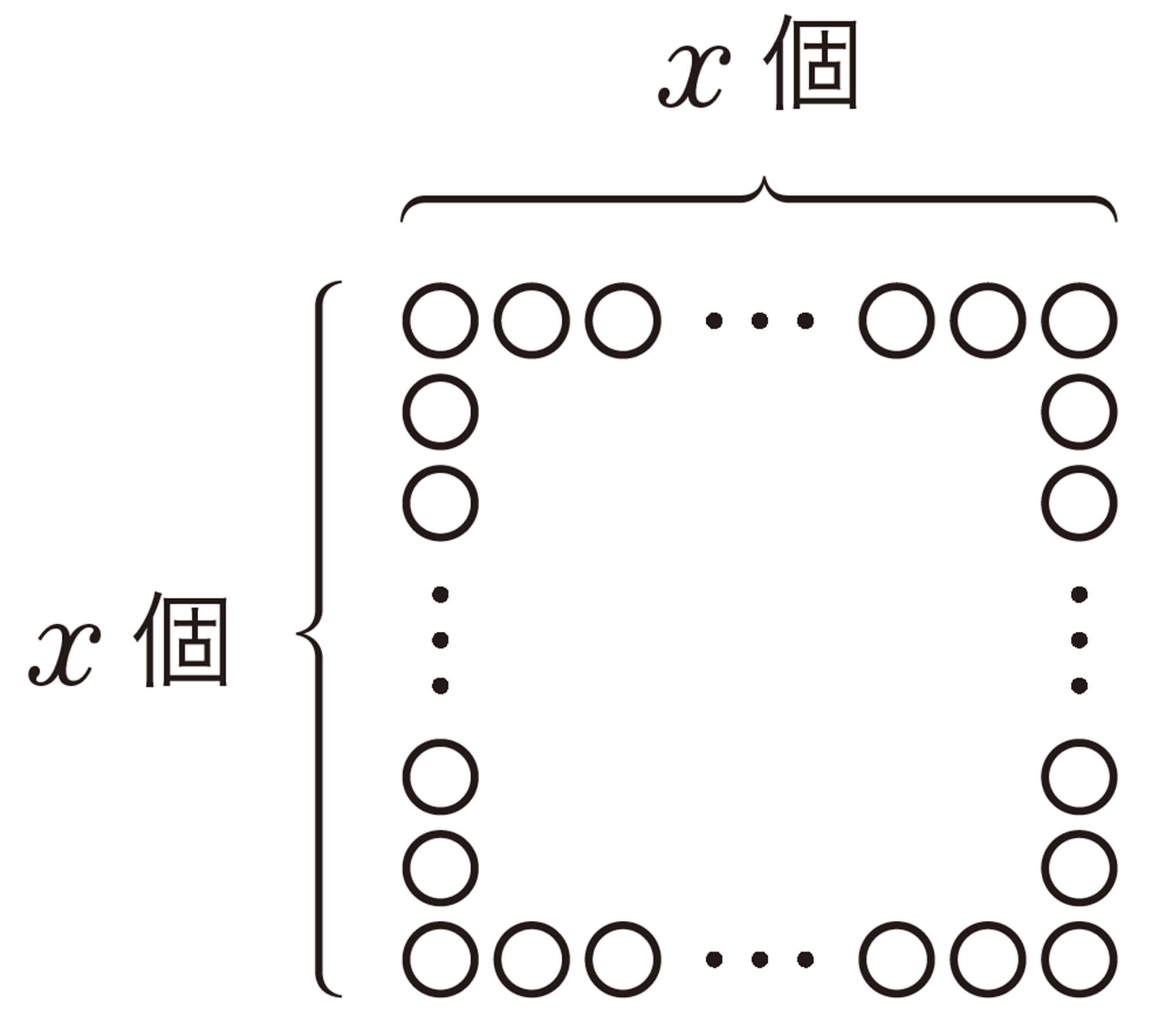
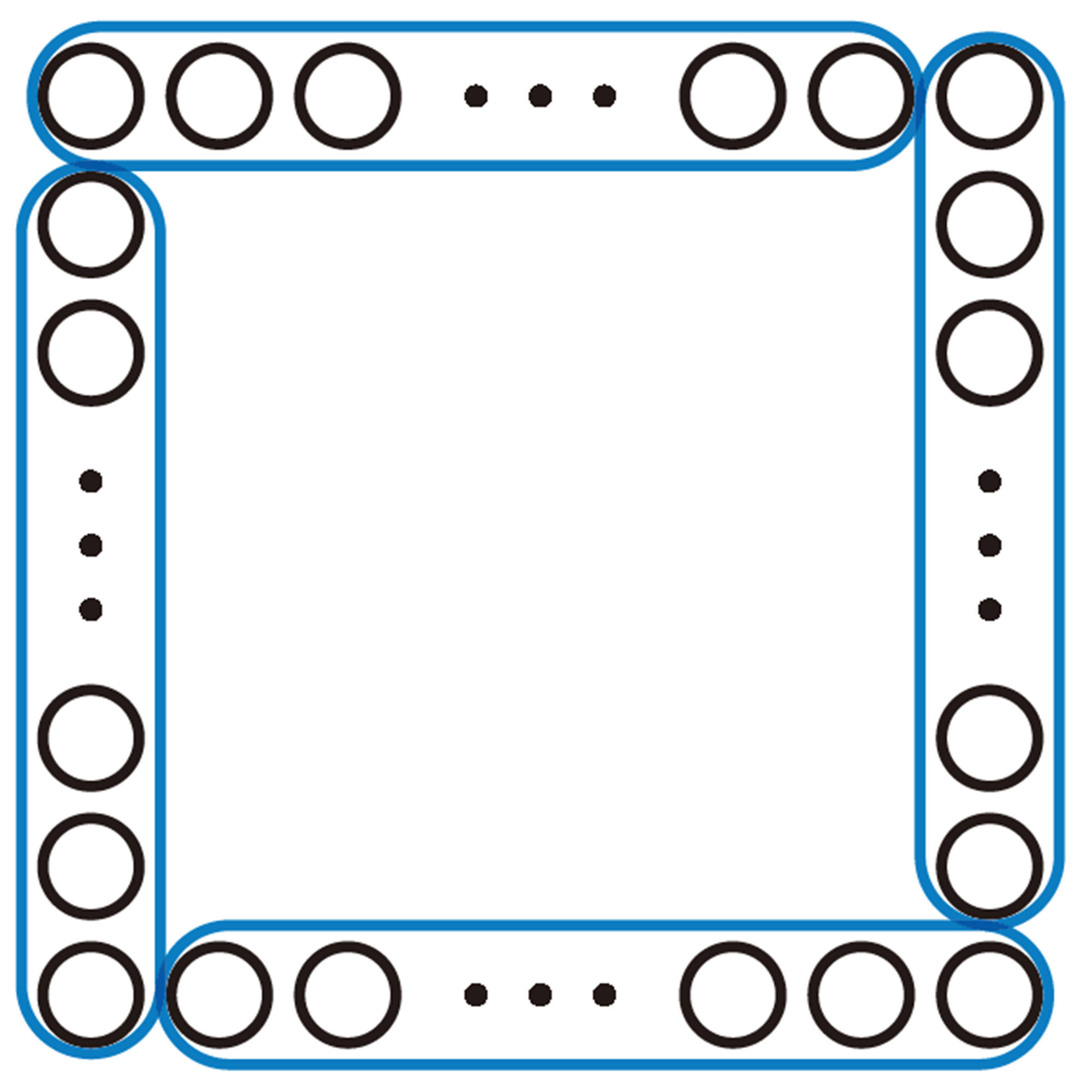
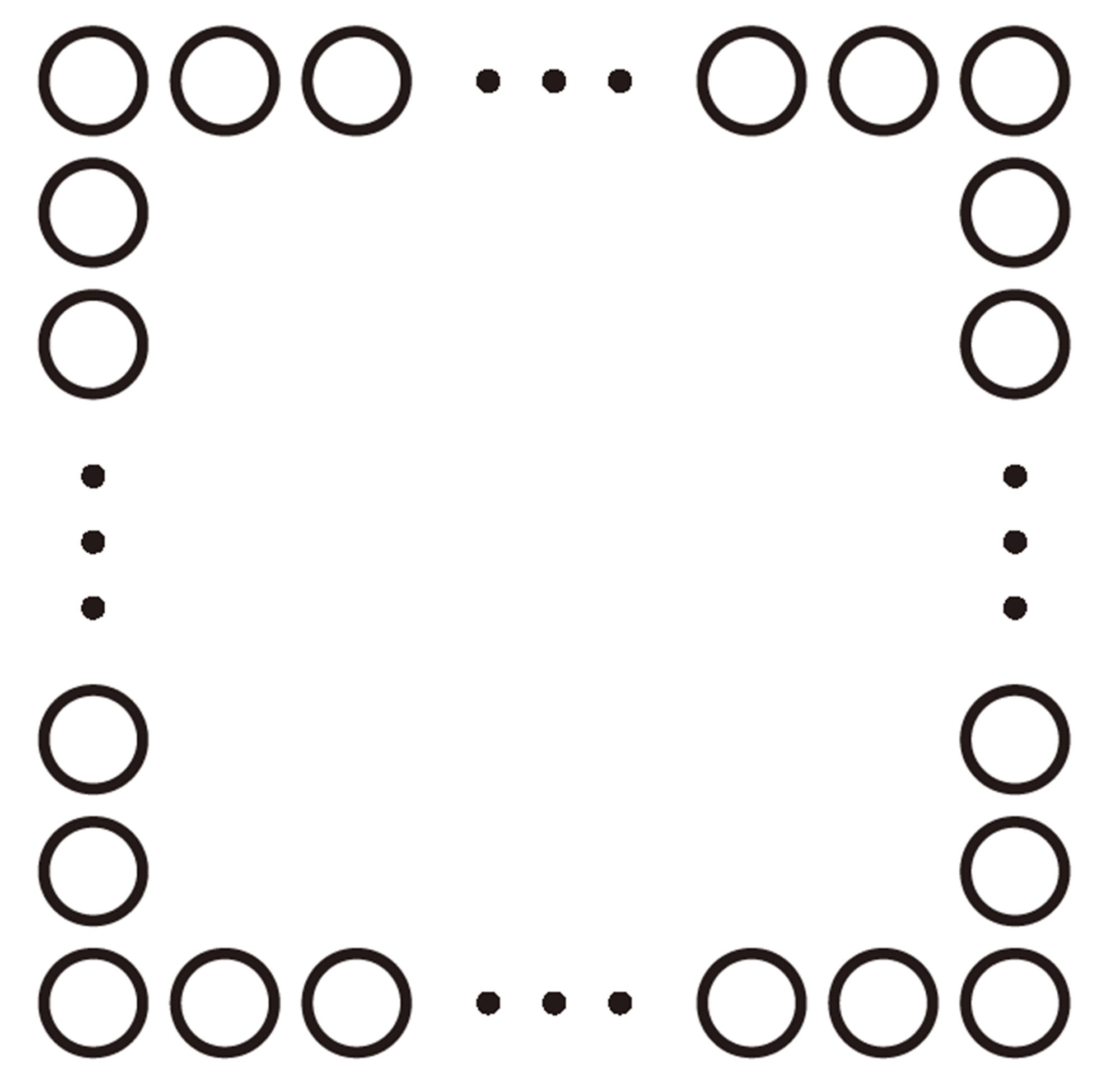
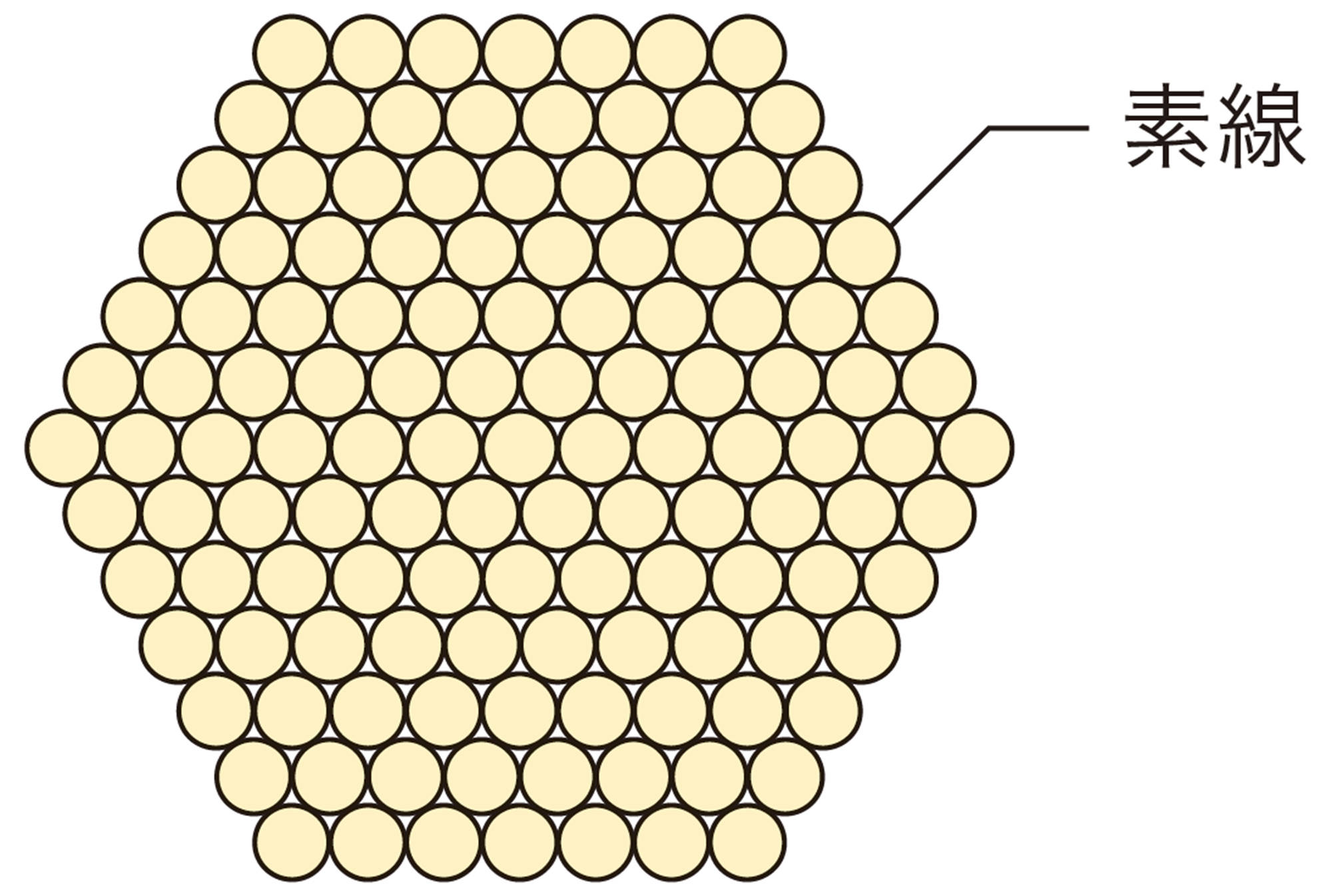
１ 広島県と愛媛県を結ぶ瀬戸内しまなみ海道には， いくつもの橋があります。この橋の中の1つである因島大橋はつり橋と呼ばれ，ケーブルを使って支えられています。ケーブルは，次のような，素線と呼ばれる針金の一種を集めたストランドから構成されています。
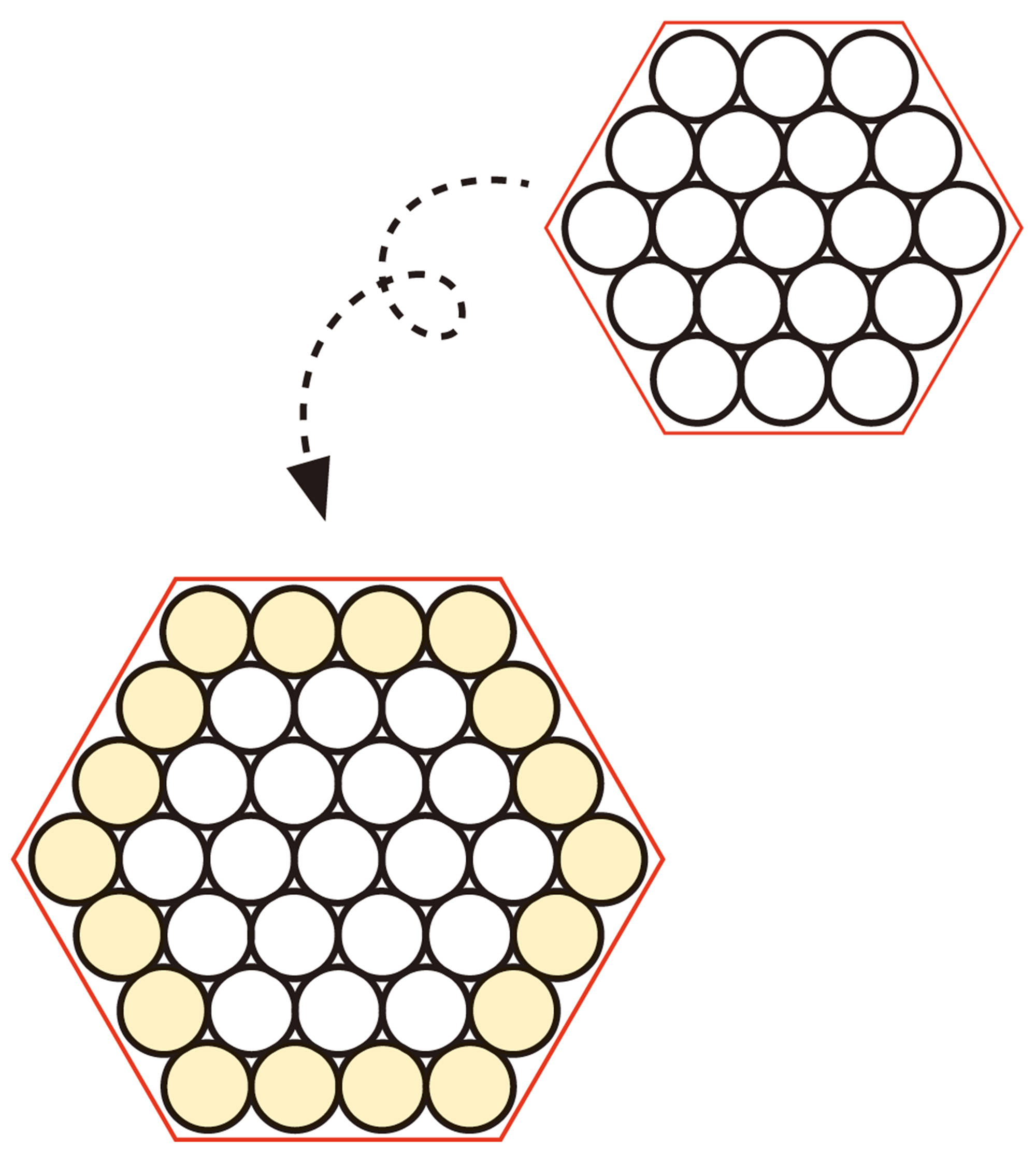
⑴ ストランドの断面は正六角形の形をしています。1辺に並ぶ素線が1本増えると，素線の総数がいくつ増えるかを，健太さんは次のように考えました。
ストランドの断面の1辺に並ぶ素線が1本増えると，素線の総数は，いちばん外側の素線の数だけ増える。たとえば，1辺に並ぶ素線が3本から4本に増えると，
[mathjax]\(4 \times 6-6=18\)
より，素線の総数は18本増える。
健太さんの考えを使って，1辺に並ぶ素線が1本増えてn本になると，素線の総数は何本増えるかを，文字式で表しなさい。
⑵ ストランドの1辺に並ぶ素線を5本にしたとき， 必要な素線の総数は何本ですか。
＞＞ 関連する職業・仕事 ［土木技術者］
<1年p.94>
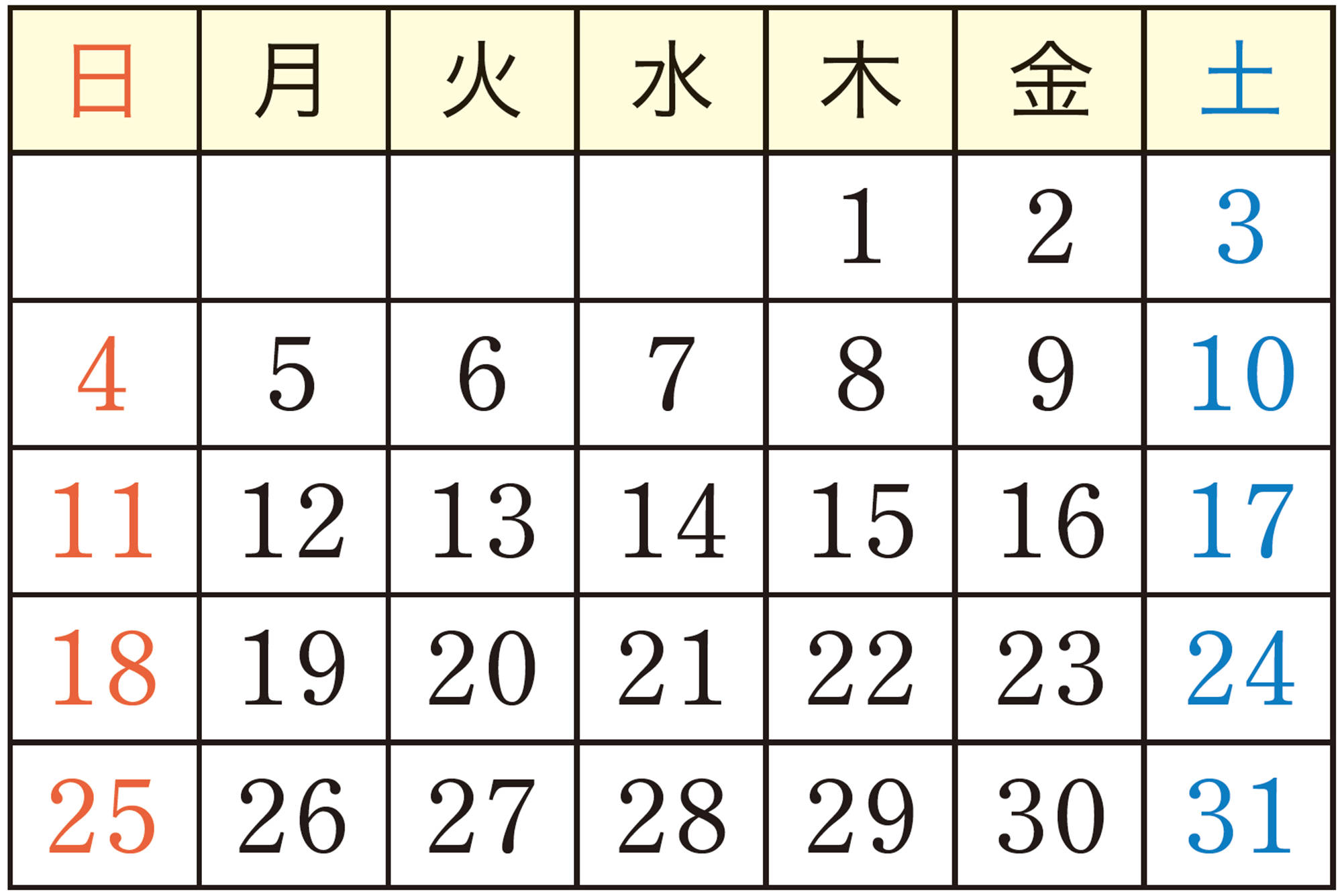
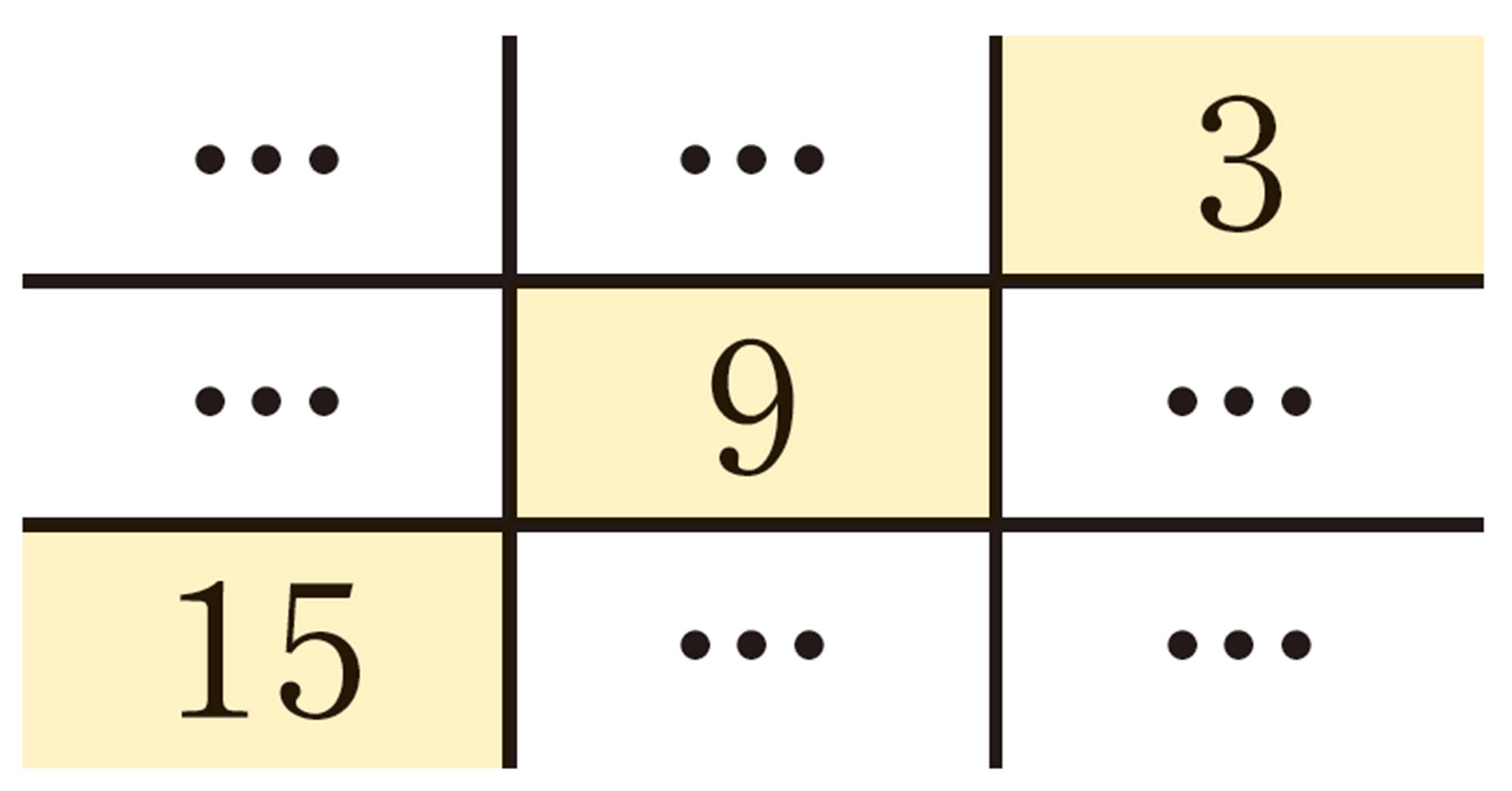
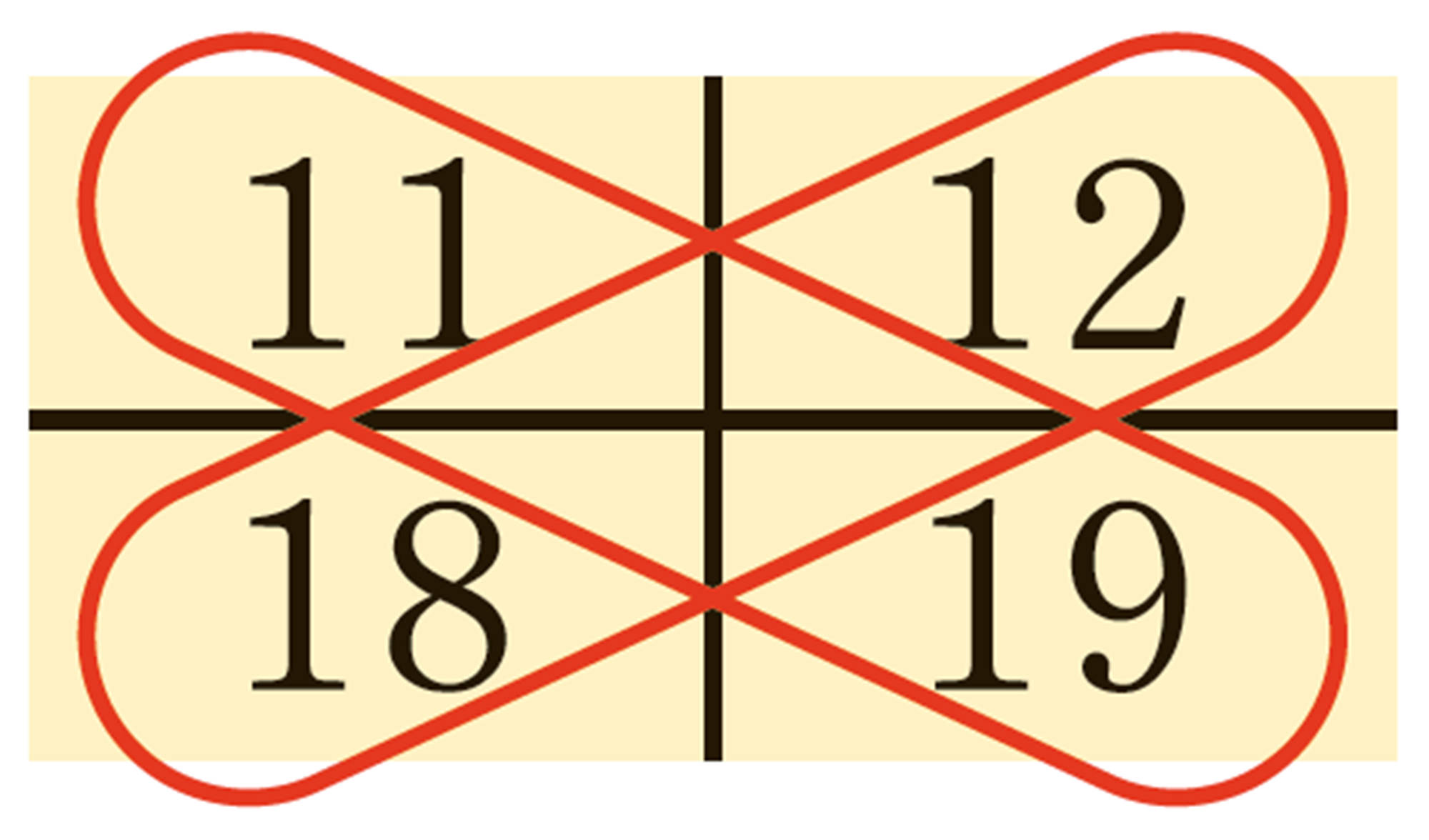
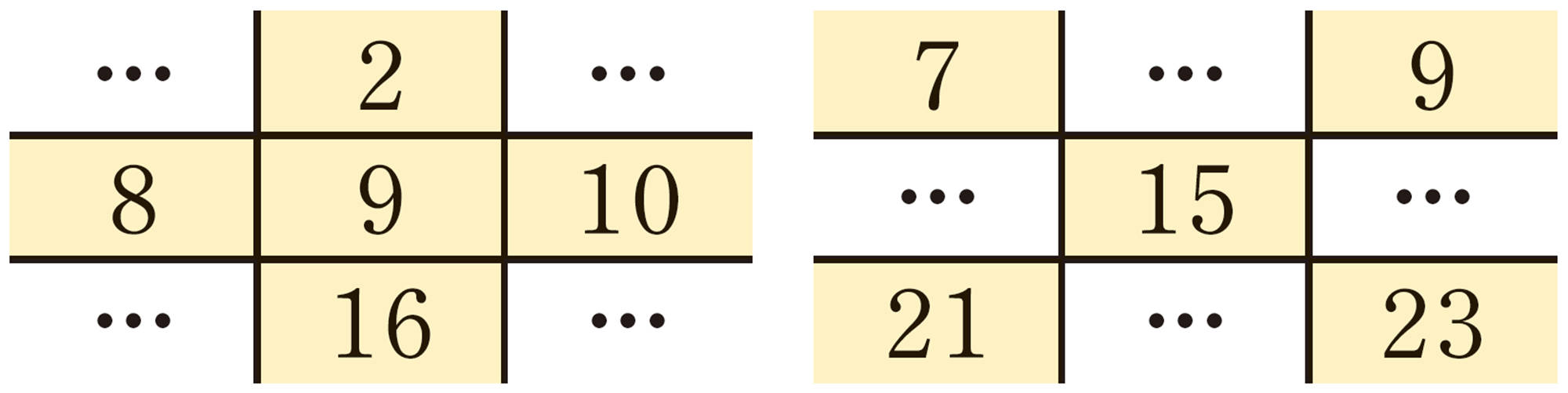
深めよう 発展 2年 カレンダーの数の秘密を考えよう
カレンダーの数に隠かくれている秘密を考えてみよう。
① 右のカレンダーの数の並びから，いろいろなきまりを見つけてみましょう。
② 拓真さんは，右のように，「縦に並んだ3 つの数の和は，中央の数の3 倍に等しい」ことに気づきました。どの場所でもそのことがいえるかどうかを，確かめてみましょう。
[mathjax]\(2+9+16=27=9 \times 3\)
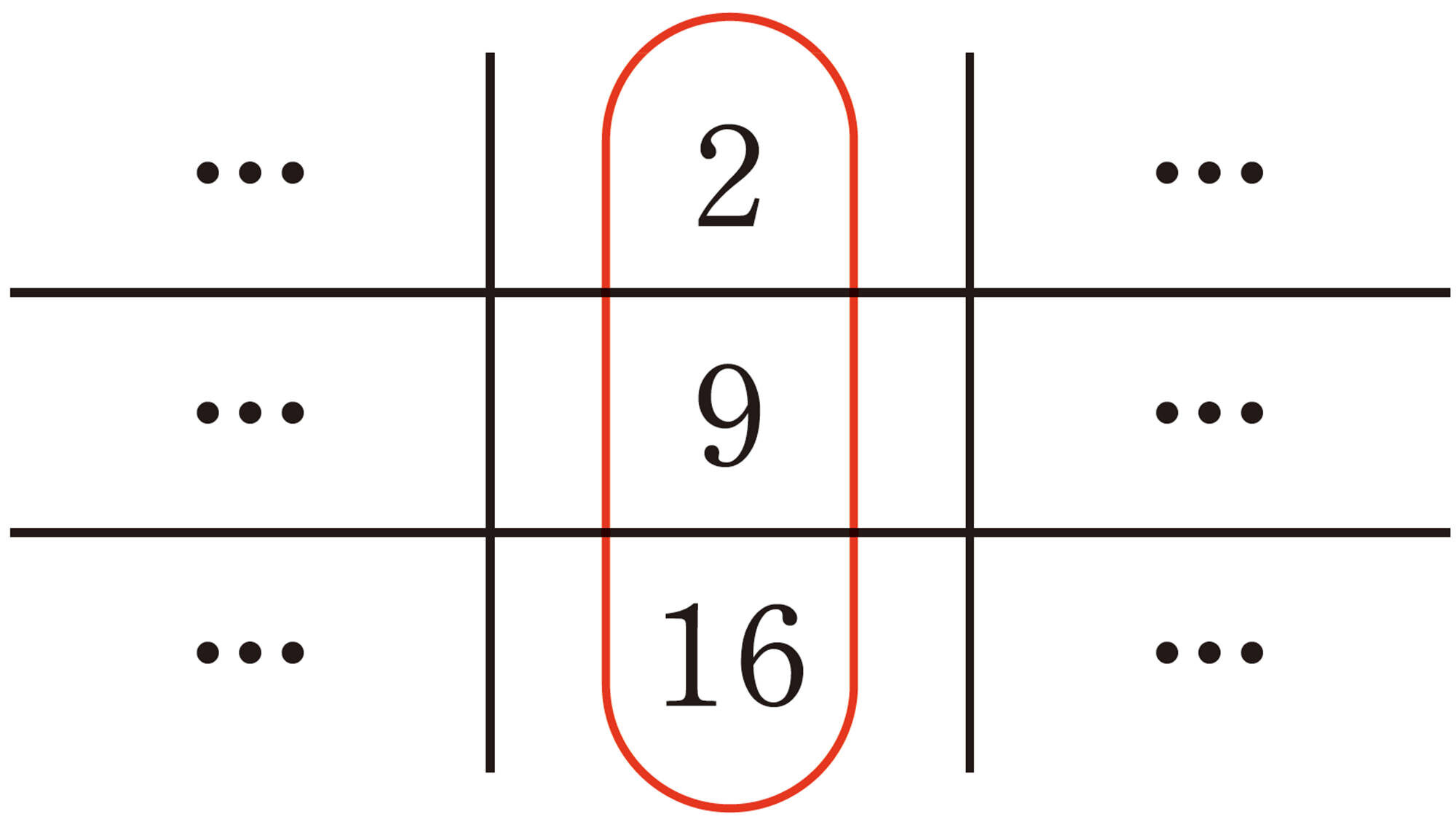
③ なぜ，②のようなことがいえるのでしょうか。拓真さんは，このことを次のように説明しました。[mathjax]\(\boxed{\phantom{00}}\)にあてはまる数を書き入れてみましょう。
縦に並ぶ3 つの数を，中央の数を基準に考えると，上の数はそれより[mathjax]\(\boxed{\phantom{00}}\)だけ小さく，下の数はそれより[mathjax]\(\boxed{\phantom{00}}\)だけ大きい。したがって，この3 つの数を加えると，[mathjax]\( -\boxed{\phantom{00}}\)と[mathjax]\( + \boxed{\phantom{00}}\)が打ち消しあって0 になり，和は中央の数の3 倍になる。
④ 縦に並ぶ3 つの数で，中央の数をa とすると，上の数と下の数はどのように表せますか。また，それらの3 つの数の和はどんな数といえるでしょうか。
⑤ ①で見つけたほかのきまりについて，説明したり，文字を使って表したりして考えてみましょう。
斜めに並ぶ3つの数の和は？
斜めの2数の和を比べると？
上のような5つの数の和は？
