<1年p.85>
２ 文字式の利用
[mathjax] \(66\)，[mathjax] \(67\)ページの問題は，いろいろな考え方で式がつくれるね。
もっとほかの考え方はないかな。
Q Question
[mathjax] \(66\)，[mathjax] \(67\)ページの問題で，正方形が5個のときのストローの本数を，大和さん，真央さんはそれぞれ次のように考えて求めました。2人の考え方を説明してみましょう。
見方・考え方
2人の考えを式に表して考えられるかな。
大和さんの考え
真央さんの考え
同じものを求めているから，同じ式ができるはずだよ。
目標 ▷ 文字式を利用して，わかりやすく説明しよう。
【１】 大和さんは，正方形がa個のときのストローの本数を求める式を，どのようにつくったかを，次のように説明しました。大和さんの説明について，気づいたことを話し合ってみましょう。
これでいいのかな？
縦向きに並べたストローの本数は，正方形の個数と同じになるからa本になる。正方形の上側にある横向きのストローの本数も，正方形の個数と同じだから，a本になる。
同じように，下側にもa本あるから，横向きのストローは全部でa本の2倍で2a本となる。したがって，全部のストローの本数を求める式は，a本と2a本を合わせるから，次のようになる。
式 3a
<1年p.86>
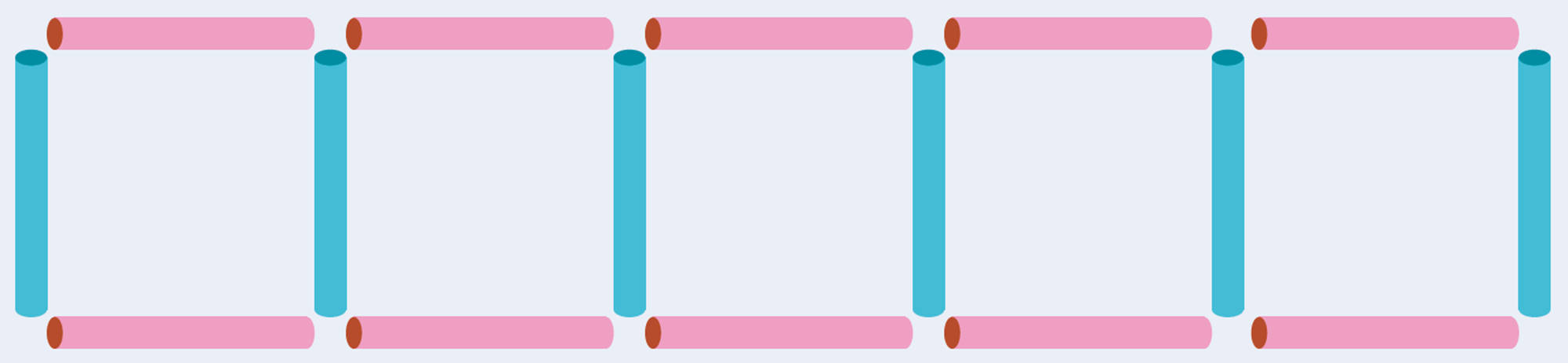
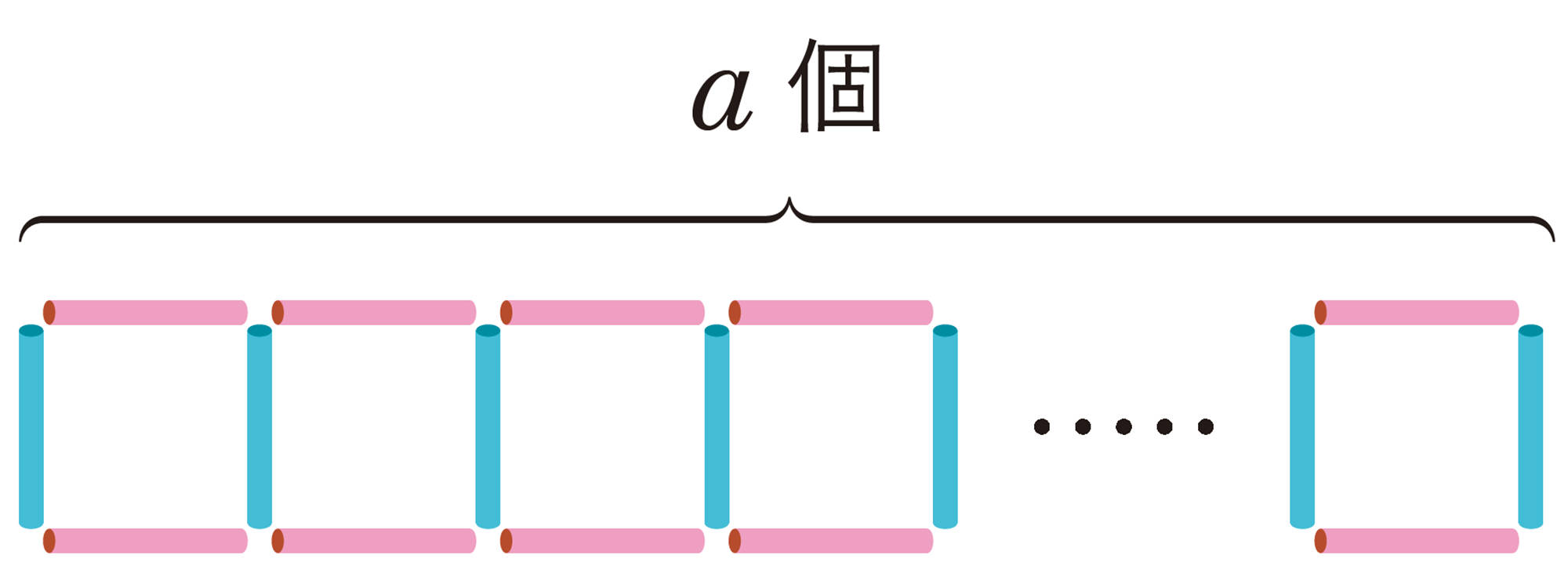
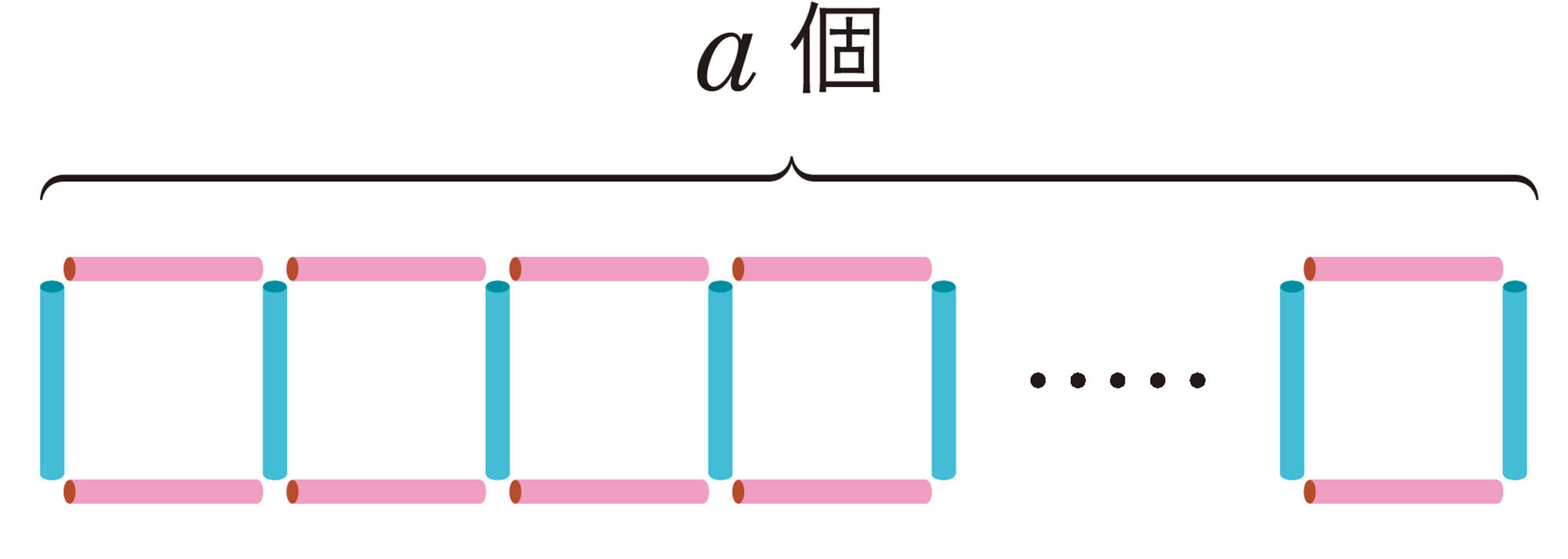
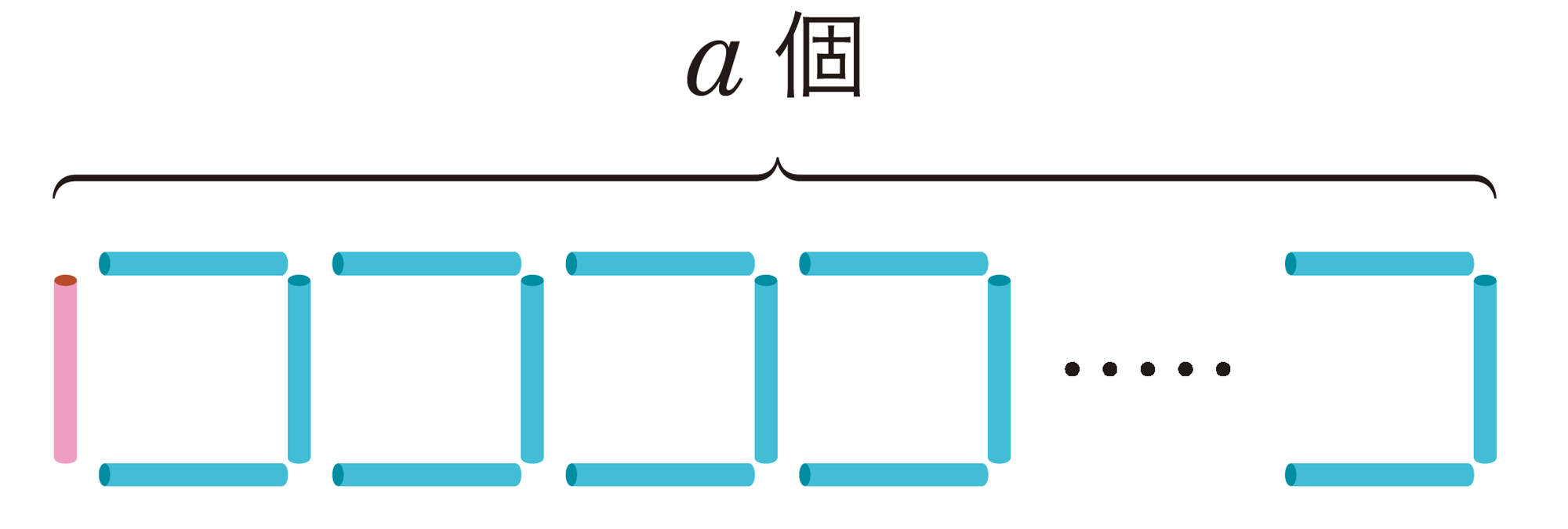
横向きのストローは，図を見ると，正方形の個数と同じになるから，上側も下側もそれぞれa本と表せるんだね。
なるほど。では，縦向きのストローの本数も，正方形の個数と関係があるのかな。
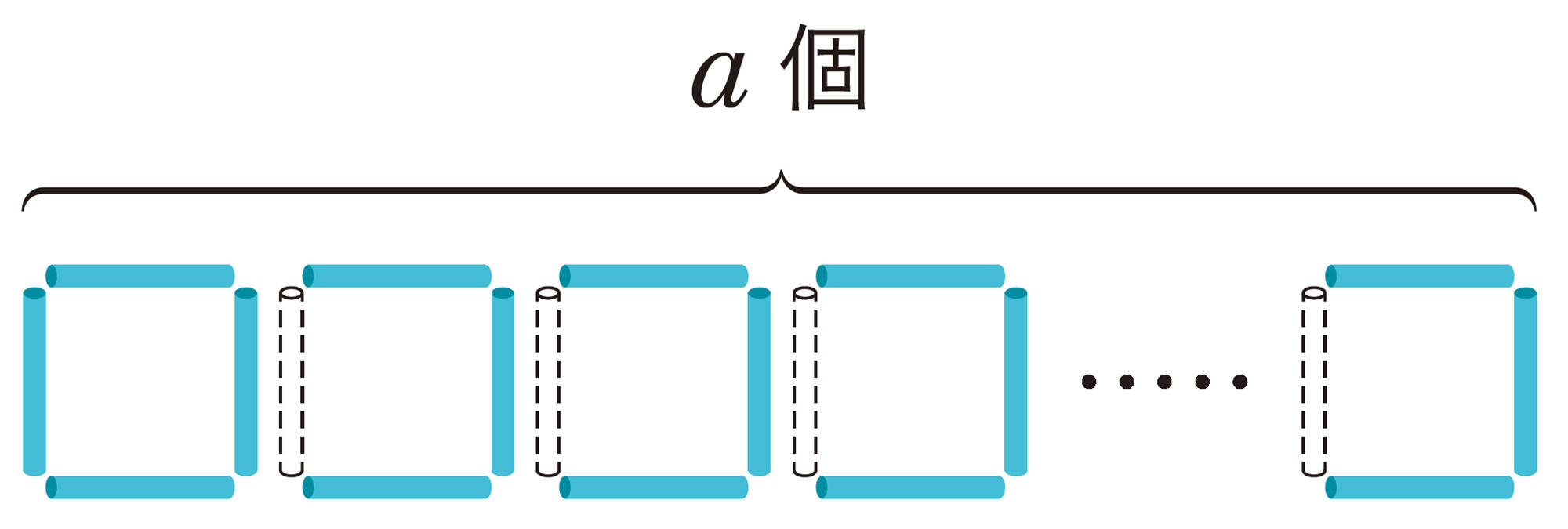
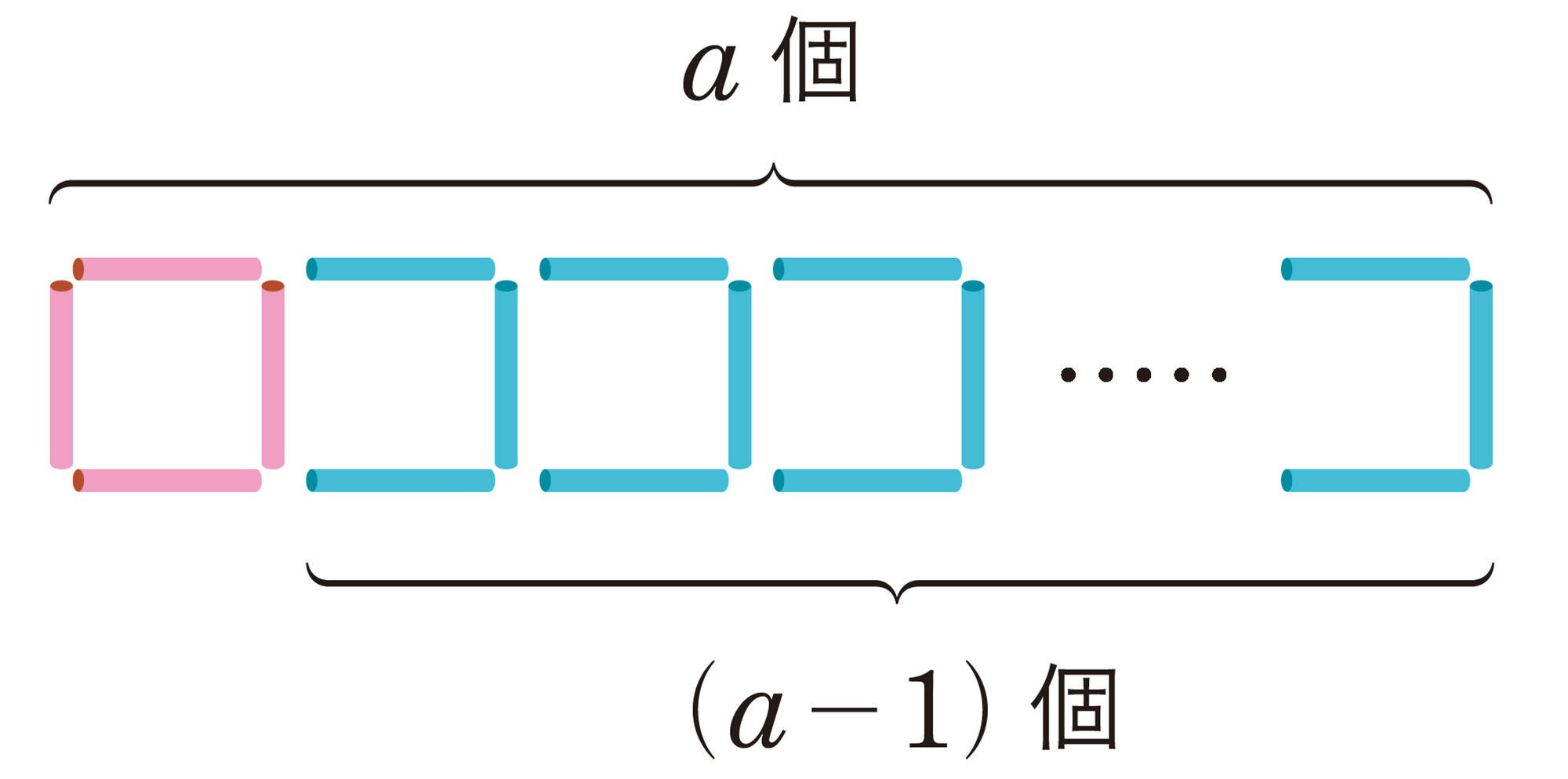
縦向きのストローが正方形の左側に1本ずつあると考えると，a本あるよ。でもそれだと，最後の正方形の右側のストローを数えていないから，それを合わせると，a本より1本多くなるね。a本より1本多いことをどうやって表せばいいのかな。
a本に1本たせばいいのだから，[mathjax]\((a+1)\)本と表せばいいよ。 文字式は本数を求める式と，求めた結果の本数の両方を表しているよ。
縦向きのストローは[mathjax]\((a+1)\)本で，横向きのストローは上下合わせて2a本だから，ストロー全部の本数を求める式は，[mathjax]\((a+1)+2a=3a+1\)になるね。美月さんの式と同じになったね。
[mathjax]\((a+1)+2a\) と表した方が，縦のストローと横のストローの数を合わせたことが，ほかの人に伝わりやすいと思う。
大和さんは，話し合った結果を次のようにまとめました。
縦向きに並べたストローは，正方形の個数に1を加えた本数だから，[mathjax]\((a+1)\)本になる。上側にある横向きに並べたストローは，正方形の個数と同じなのでa本，それが上下に2列あるので，2a本になる。したがって，ストローの本数を求める式は，次のようになる。
式 [mathjax]\((a+1)+2a\)
【２】 真央さんの考え方で，正方形がa個のときのストローの本数を求める式をつくってみましょう。また，式のつくりかたを説明してみましょう。
<1年p.87>
【３】 68ページの【Q】の美月さんや69ページの問2の拓真さんの考え方では，正方形がa個のときのストローの本数を求める式は，それぞれ次のようになりました。
美月さん
式 [mathjax]\(1+3a\)
拓真さん
式 [mathjax]\(4+3(a-1)\)
拓真さんの式，【2】の真央さんの式をそれぞれ計算し，その結果を美月さんの式と比べてみましょう。
文字を使って表すと，いろいろな考え方をしても，1つの式にまとめられるね。
正方形を正三角形に変えたら，式のどこが変わりそうかな。
【４】 次のように，同じ長さのストローを使って，正三角形を横につないだ形をつくります。正三角形をa個つくるとき，ストローは何本必要でしょうか。いろいろな考え方で式をつくってみましょう。
つくった式を計算してみよう。
【５】 ストローの本数を文字式を利用して考えると，どんなよさがあると考えられるでしょうか。これまでに学んだことをふりかえって，まとめてみましょう。
どんなことがわかったかな
文字式を利用することで，いろいろな考え方を文字式で表したり，簡単な式にまとめたりすることができます。
<1年p.88>
１ 次の式の項をいいなさい。また，文字をふくむ項の係数をいいなさい。
⑴ [mathjax]\(-5x+9\)
⑵ [mathjax]\(\dfrac{a}{3}-5\)
２ 次の計算をしなさい。
⑴ [mathjax]\(2a-9a\)
⑵ [mathjax]\(4x+x\)
⑶ [mathjax]\(3a-7+6a-1\)
⑷ [mathjax]\(-x+9+5x-2\)
３ 次の計算をしなさい。
⑴ [mathjax]\((3a+1)+(5a-8)\)
⑵ [mathjax]\((2x-4)+(-x+6)\)
⑶ [mathjax]\((x-7)-(-8x+3)\)
⑷ [mathjax]\((-3a-5)-(-9a-7)\)
４ 次の計算をしなさい。
⑴ [mathjax]\(4a \times (-2)\)
⑵ [mathjax]\(2(3x-7)\)
⑶ [mathjax]\((x-8) \times (-3)\)
⑷ [mathjax]\(\dfrac{2x-1}{3} \times 6\)
⑸ [mathjax]\((-18a) \div 6\)
⑹ [mathjax]\((20a-12) \div 4\)
５ 次の計算をしなさい。
⑴ [mathjax]\(2(3a-4)+3(a+2)\)
⑵ [mathjax]\(6(5x+3)+4(-7x-4)\)
⑶ [mathjax]\(7(x+2)-4(2x-5)\)
⑷ [mathjax]\(-2(-3a+1)-5(a-8)\)
[mathjax]\(2x²\)や[mathjax]\(-5ab\)のように，2つの文字と数との積で表される項を2次の項といいます。また，次のように2次の項と1次の項，数の項の和の式や，2次の項だけの式を2次式といいます。
例 ［ 2次式 ］ [mathjax]\(3x²+2x+1\)，[mathjax]\(-4xy+3\)，[mathjax]\(ab+c\)，[mathjax]\(5a²\)
