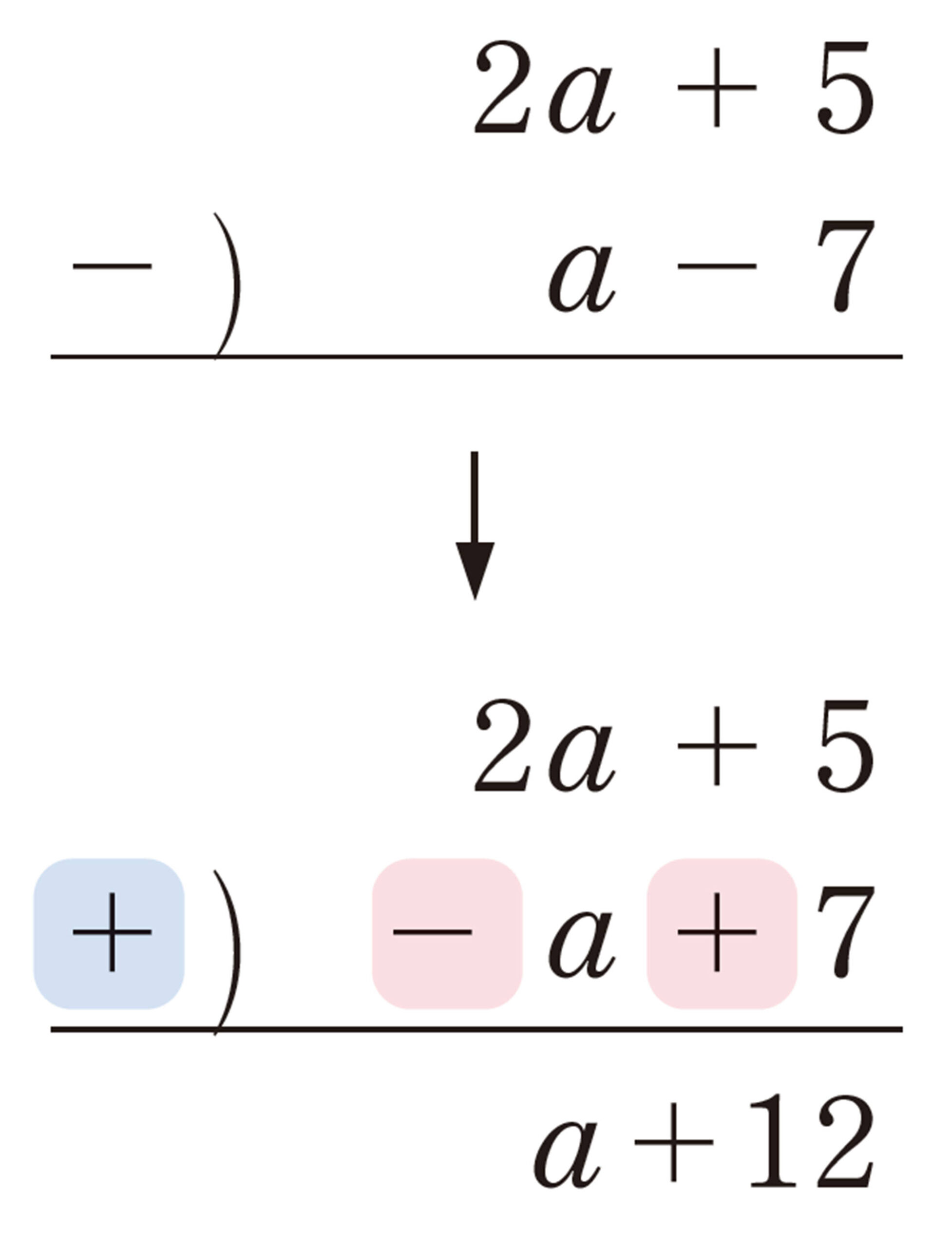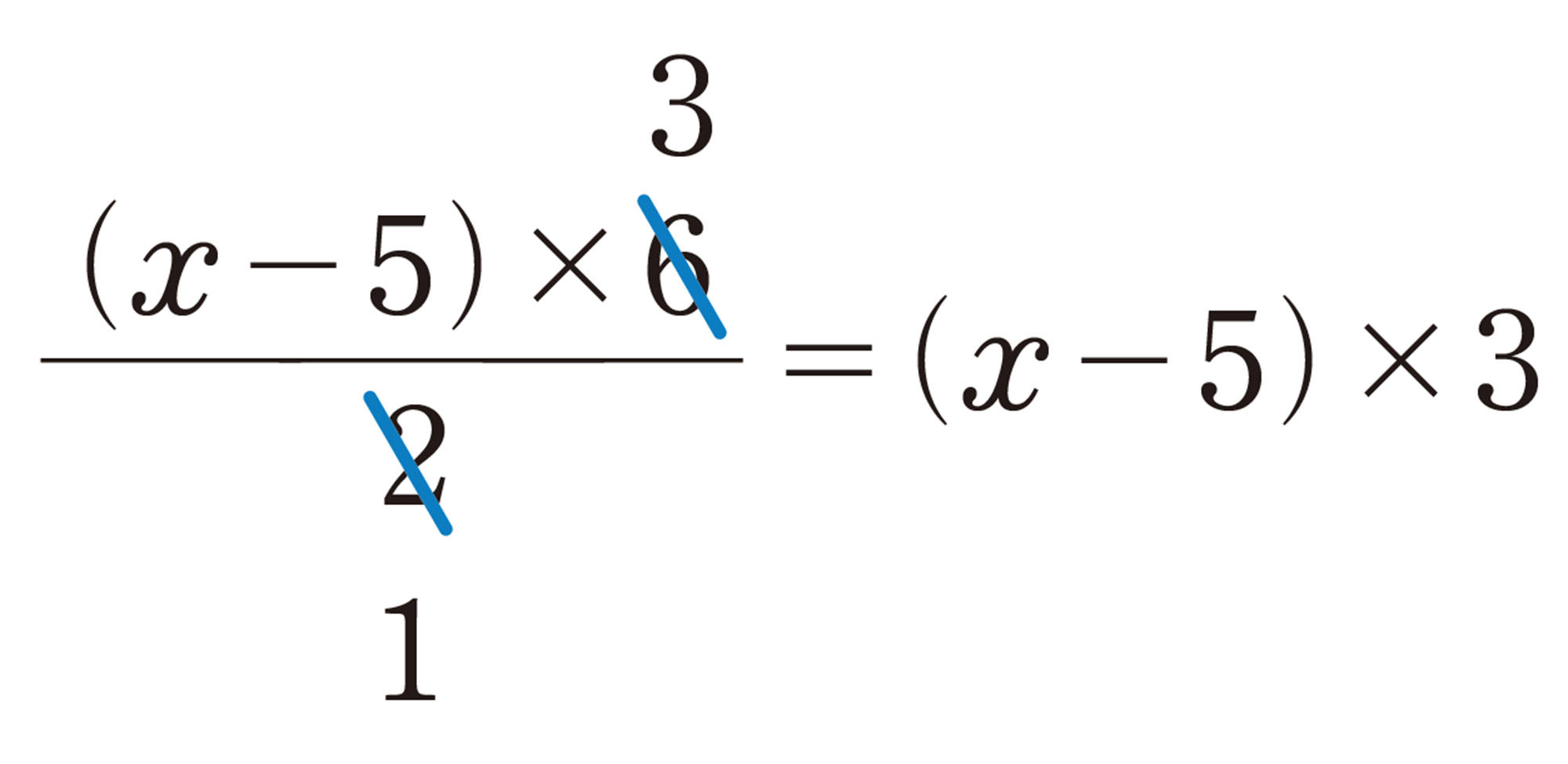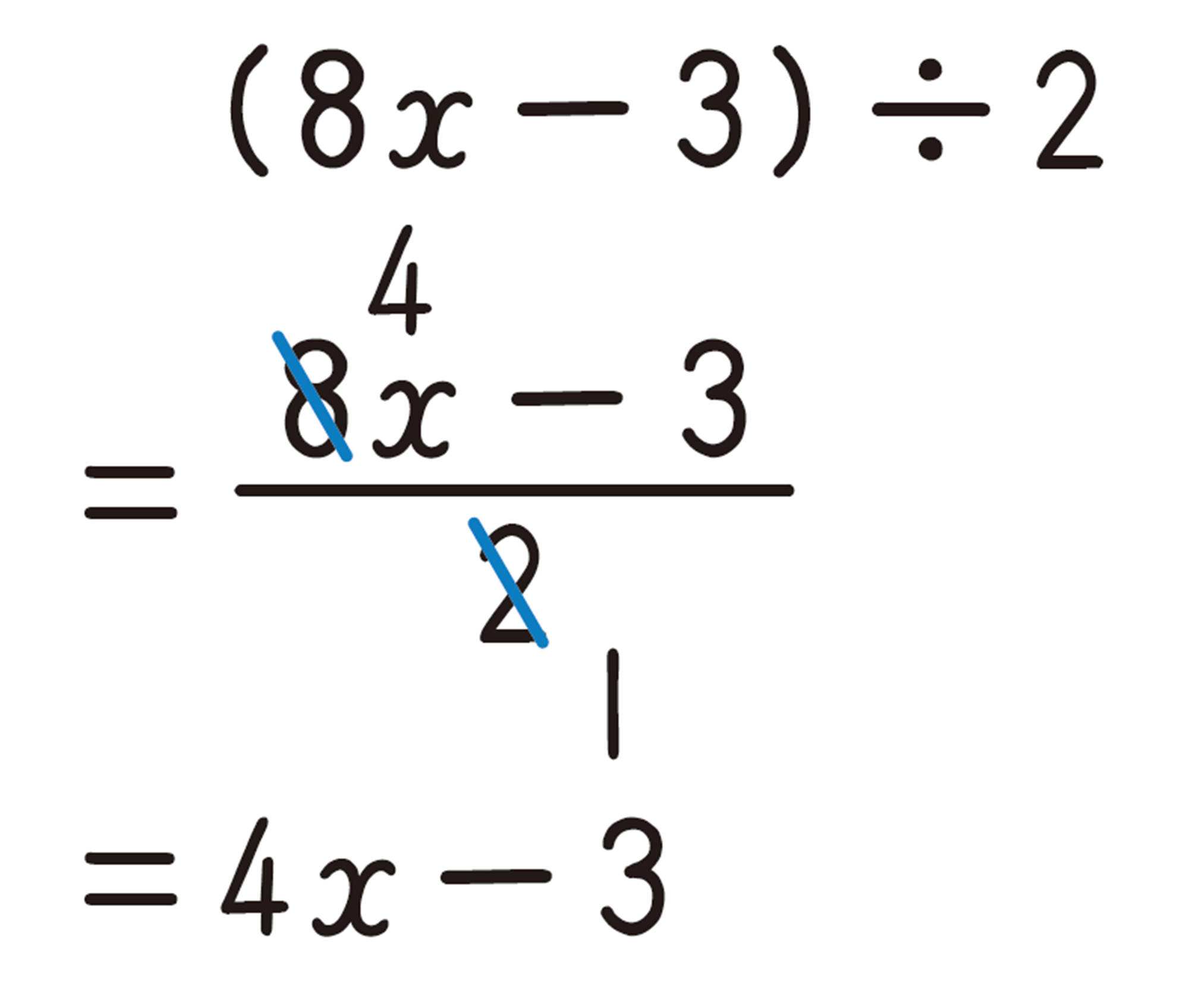<1年p.79 >
2節 式の計算
なぜ式がちがうのかな？
[mathjax] \(66\)，[mathjax] \(67\)ページの問題で，正方形5個のときのストローの本数を求めるのに，いくつかのちがう式ができました。
【１】 次の2つの式は，右の長方形のまわりの長さを表しています。このことから，どんなことがわかるか考えてみましょう。
㋐ [mathjax]\(2a+6\)
㋑ [mathjax]\(a+a+3+3\)
㋐と㋑は同じ式と考えていいのかな。
次の課題へ！
文字をふくんだ式も，計算できるのかな？
P. 79
１ 1次式の計算
項と係数
目標 ▷ 文字式のまとめ方について考えよう。
[mathjax]\(2a+6\)という式で，加法の記号[mathjax]\(+\)で結ばれた[mathjax] \(2a\)，[mathjax] \(6\)を，この式の 項 という。また，文字をふくむ項[mathjax]\(2a\)で，数の部分[mathjax]\(2\)を[mathjax]\(a\)の 係数 という。
例 １ [mathjax]\(-3x-5=-3x+(-5)\)であるから，
式 [mathjax]\(-3x-5\)の項は，[mathjax] \(-3x\)，[mathjax] \(-5\)
項 [mathjax] \(-3x\)で，xの係数は，[mathjax] \(-3\)
正の数，負の数で考えたように，和の形に直すと項がわかりやすくなるね。
問 １ 次の式の項をいいなさい。また，文字をふくむ項の係数をいいなさい。
⑴ [mathjax]\(5a-20\)
⑵ [mathjax]\(-9a+8\)
⑶ [mathjax]\(4-x\)
⑷ [mathjax]\(\dfrac{x}{2}+7\)
<1年p.80 >
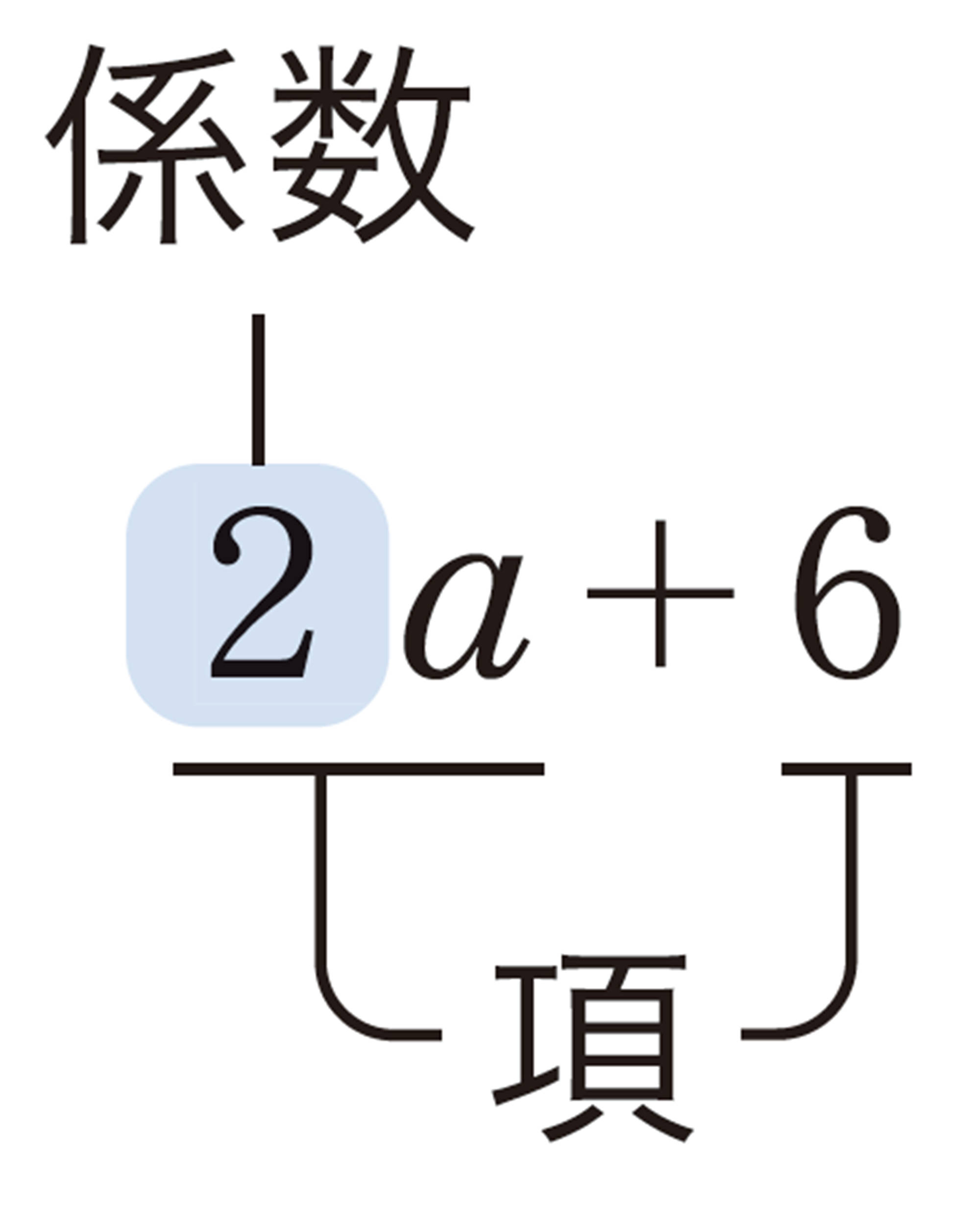
2aや[mathjax] \(-3x\)のように，1つの文字と正の数や負の数との積で表される項を 1次の項 という。
[mathjax]\(2a+6\)のように，1次の項と数の項との和の式や，2aのように，1次の項だけの式を 1次式 という。
おしえて！
P.88
2次の項や2次式もあるのかな？
問 ２ 次の式のうち，1次式はどれですか。
㋐ [mathjax] \(-8x\)
㋑ [mathjax]\(x²+1\)
㋒ [mathjax]\(2a+8\)
㋓ [mathjax]\(\dfrac{2}{5}a-7\)
例 ２ [mathjax]\(3a+2a\)，[mathjax]\(3a-2a\)は，分配法則により，次のようにまとめることができる。
⑴
⑵
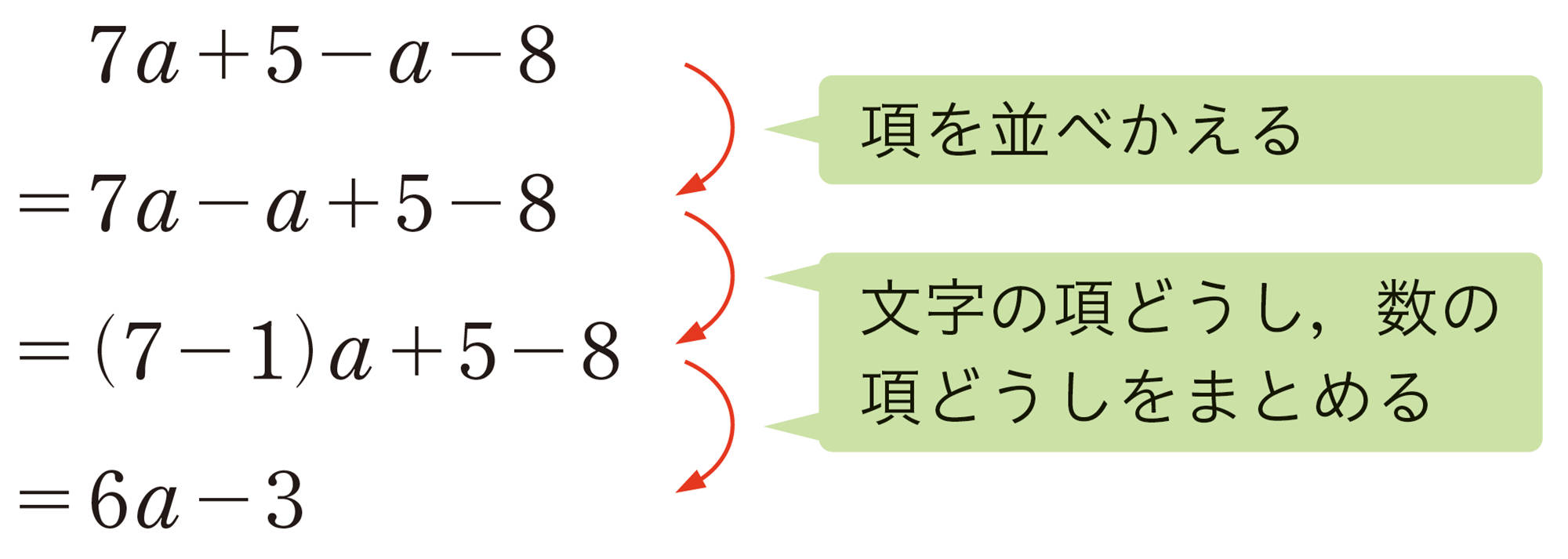
前ページの1 で考えたように，1つの式の中の同じ文字は同じ数を表している。 したがって， 文字の部分が同じ項があるとき，分配法則を使って，1つの項にまとめることができる。
問 ３ 次の計算をしなさい。
⑴ [mathjax]\(5x+2x\)
⑵ [mathjax]\(9a-6a\)
⑶ [mathjax]\(-7b+b\)
⑷ [mathjax]\(-y-4y\)
⑸ [mathjax]\(0.4x+0.6x\)
⑹ [mathjax]\(\dfrac{4}{5}a- \dfrac{1}{5}a\)
例 ３
項を並べかえる
文字の項どうし，数の項どうしをまとめる
問 ４ 次の計算をしなさい。
⑴ [mathjax]\(4x+7+5x+8\)
⑵ [mathjax]\(-3a+5+9a-2\)
⑶ [mathjax]\(2x-12-6x+15\)
⑷ [mathjax]\(-a+2-3-8a\)
やってみよう
計算力を高めよう3-1
P.89
どんなことがわかったかな
分配法則を使うと，文字の部分が同じ 1次の項をまとめることができます。
次の課題へ！
同じ文字をふくむ項がまとめられるなら，いろいろな計算ができるのかな？
P.81
<1年p.81>
1次式どうしの加法・減法
Q Question
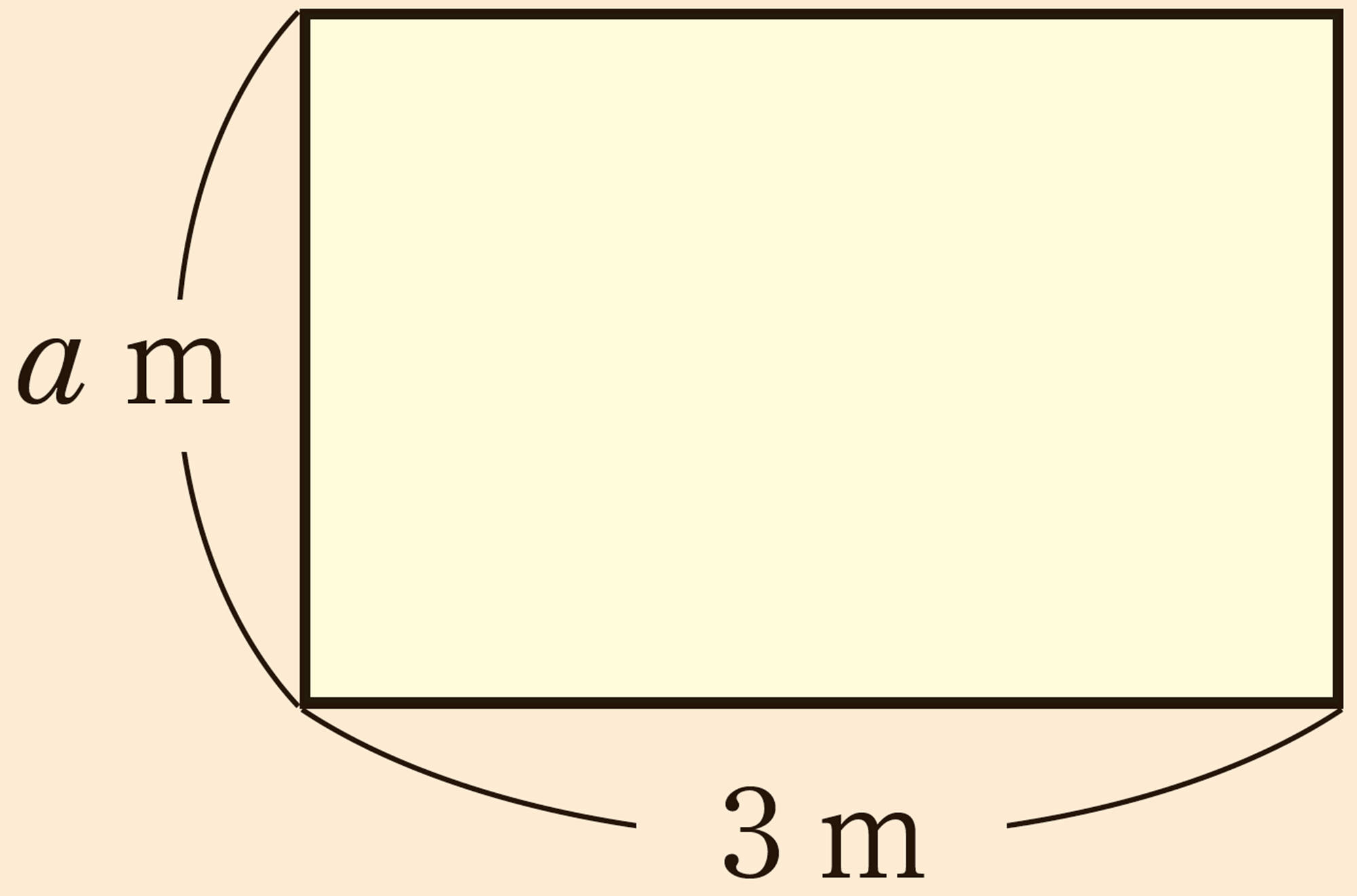
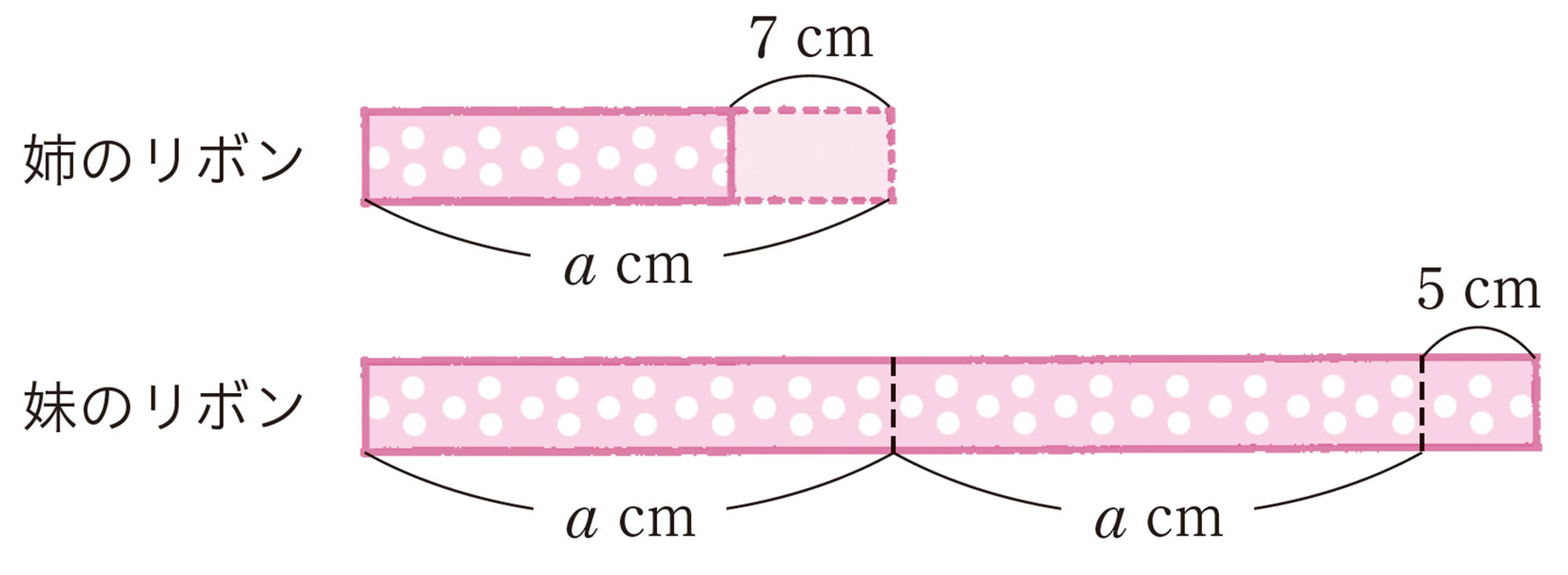
姉のリボンからacm の長さをとろうとすると7cmたらず，妹のリボンからacm の長さを2回とると5cm あまります。このとき，次のことを考えてみましょう。
⑴ 2人のリボンを合わせると何 cm になるでしょうか。
⑵ 妹のリボンは姉のリボンより何 cm 長いでしょうか。
同じ文字の項はまとめられたね。
1次式どうしの計算も，まとめていいのかな。
見方・考え方
1 次式どうしの加法や減法も，数の計算と同じようにできるかな。
目標 ▷ 1次式の計算を考えよう。
例 ４
縦書きの計算では，文字の項，数の項を，それぞれ縦にそろえて書こう。
1次式の加法では，2つの式の同じ文字の項どうし，数の項どうしをそれぞれまとめて，1つの1次式をつくる。
問 ５ 次の計算をしなさい。
⑴ [mathjax]\((5x-4)+(3x-6)\)
⑵ [mathjax]\((2x+9)+(4x-3)\)
⑶ [mathjax]\((3a+5)+(-2a+8)\)
⑷ [mathjax]\((-7a-1)+(a+4)\)
⑸ [mathjax]\((-7+5x)+(2-5x)\)
⑹ [mathjax]\(\require{physics} \left(\dfrac{3}{5}x-\dfrac{2}{3}\right)+\require{physics} \left(\dfrac{2}{5}x+\dfrac{1}{3}\right)\)
<1年p.82>
例 ５
1次式の減法では，ひく式の各項の符号を変えて，加法に直して計算すればよい。
問 ６ 次の計算をしなさい。
⑴ [mathjax]\((7x+2)-(3x-1)\)
⑵ [mathjax]\((x-8)-(2x-5)\)
⑶ [mathjax]\((-4a+9)-(a+3)\)
⑷ [mathjax]\((5a+6)-(-2a+6)\)
⑸ [mathjax]\((7-x)-(2x+8)\)
⑹ [mathjax]\(\require{physics} \left(\dfrac{1}{3}x-2\right)-\require{physics} \left(\dfrac{1}{2}x-5\right)\)
やってみよう
計算力を高めよう3-2
P.89
項が1つの1次式と数の乗法・除法
例 ６
⑴
⑵
問 ７ 次の計算をしなさい。
⑴ [mathjax]\(6x \times 2\)
⑵ [mathjax]\((-7) \times 2y\)
⑶ [mathjax]\(-3a \times 4\)
⑷ [mathjax]\(-b\times (-9)\)
⑸ [mathjax]\(10\times 0.8x\)
⑹ [mathjax]\(\dfrac{3}{2}a \times 6\)
例 ７ [mathjax]\(6x \div 4\)の計算をしなさい。
解答
方法①
方法②
注意 例7の答えは，[mathjax]\(\dfrac{3}{2}x\)と[mathjax]\(\dfrac{3x}{2}\)のどちらの表し方でもよい。また，項[mathjax]\(\dfrac{3}{2}x\)としたときの係数[mathjax]\(\dfrac{3}{2}\) は，仮分数のままにしておく。
問 ８ 次の計算をしなさい。
⑴ [mathjax]\(8x \div 2\)
⑵ [mathjax]\(12x \div (-4)\)
⑶ [mathjax]\(-10x \div (-5)\)
⑷ [mathjax]\(-a \div 5\)
⑸ [mathjax]\(9x \div 12\)
⑹ [mathjax]\(15x \div \require{physics} \left(-\dfrac{3}{2}\right)\)
<1年p.83>
項が2つの1次式と数の乗法・除法
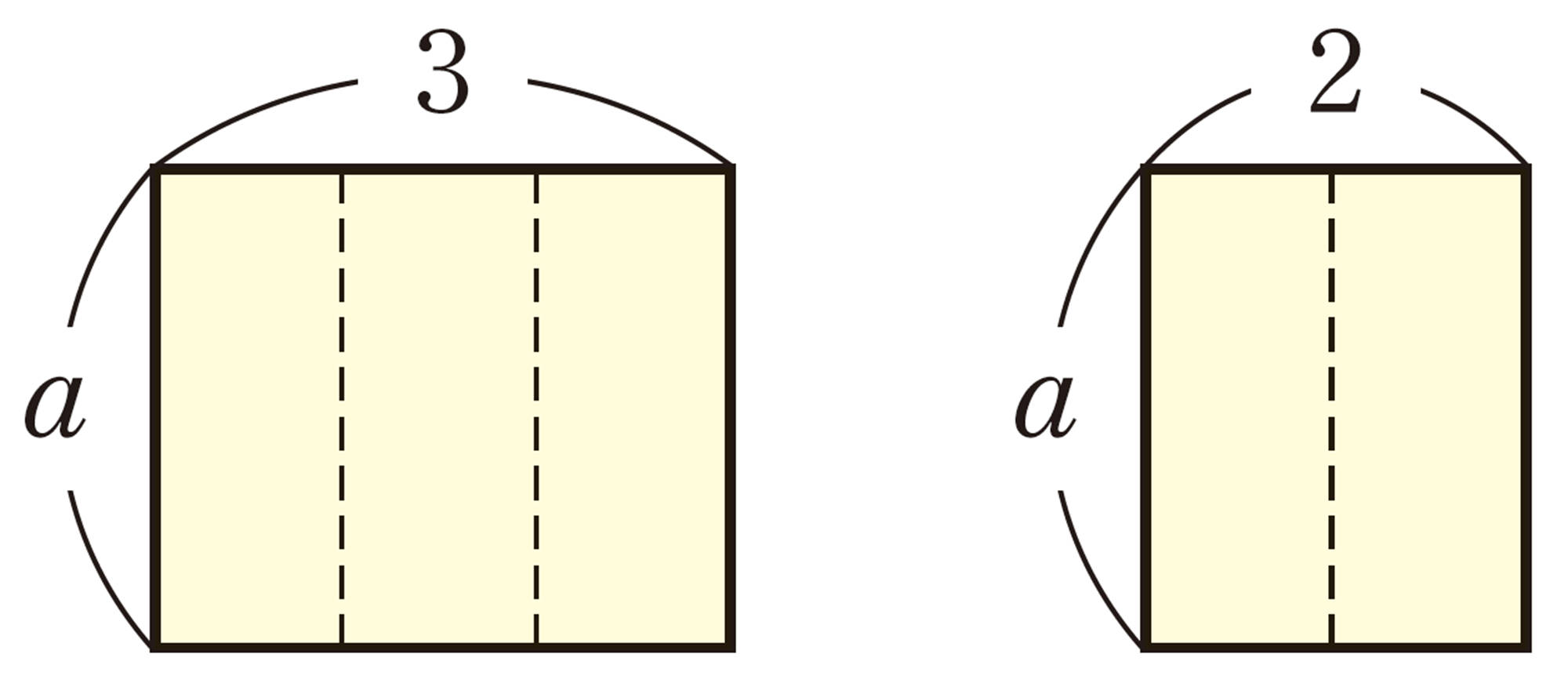
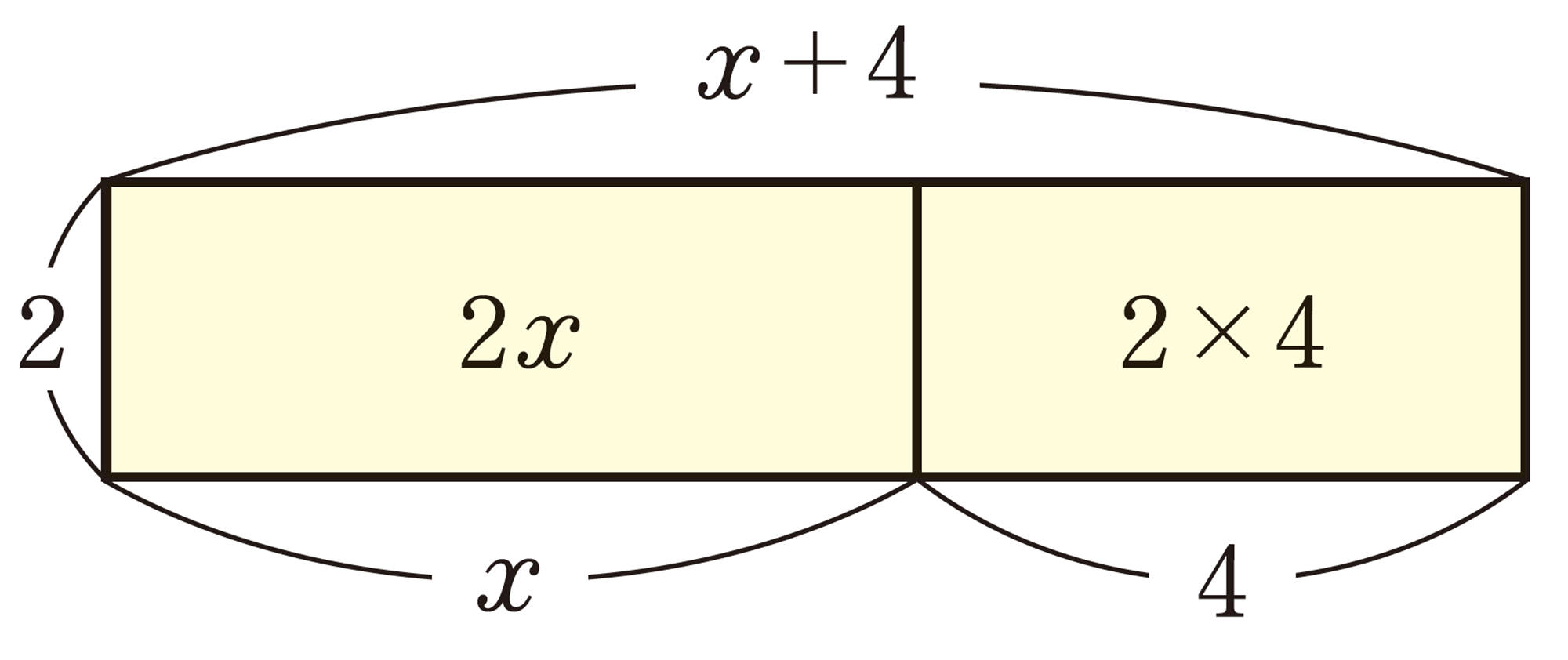
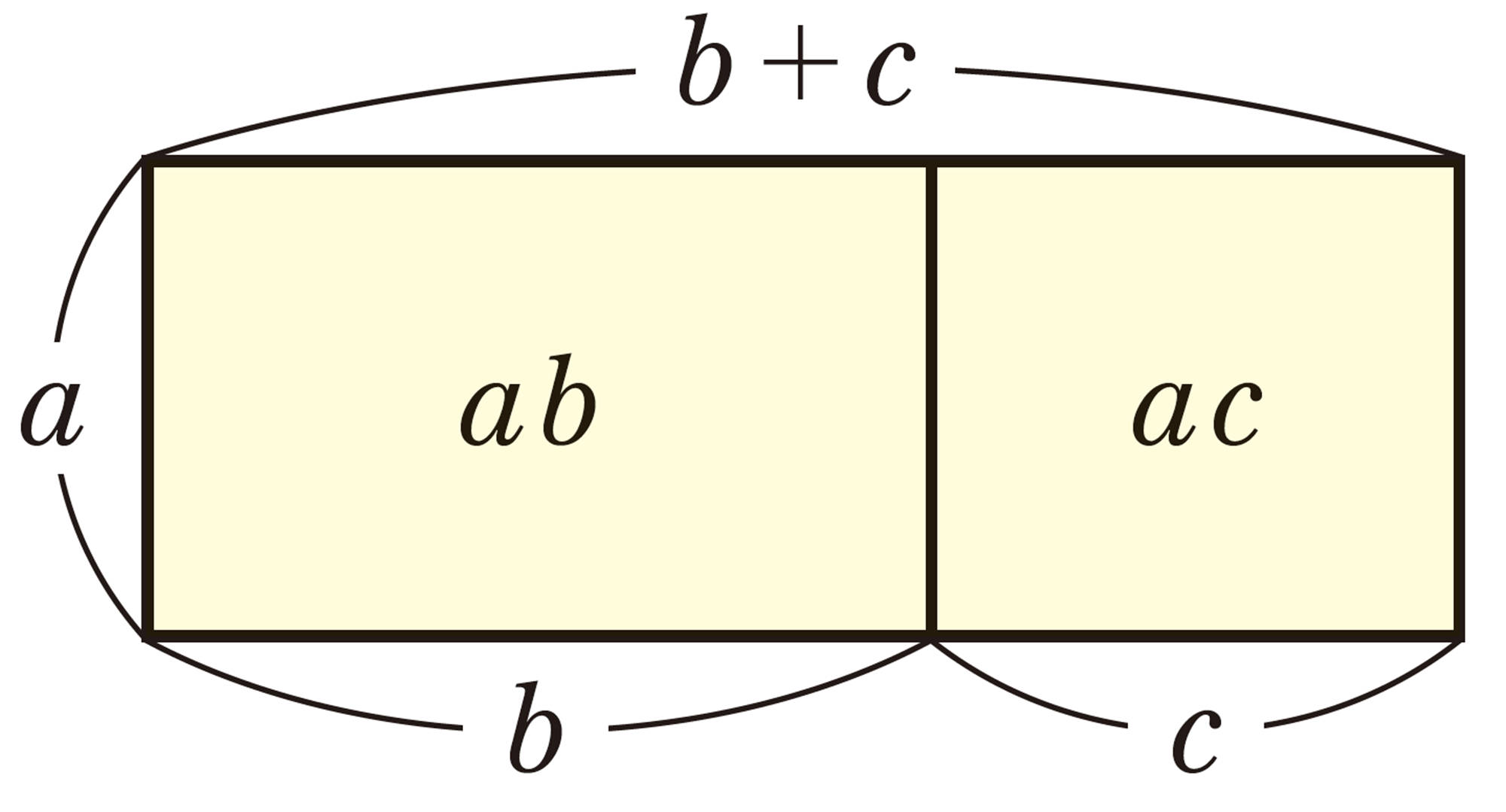
Q Question
縦2cm，横xcm のタイルと縦2cm，横 4cm のタイルを並べたときの面積は，どのように求めたらよいでしょうか。
図を見れば，2つの式で表せることがわかるね。
1次式でも，分配法則は成り立つのかな。
見方・考え方
1次式と数の乗法も，数の計算と同じようにできるかな。
項が2つの1次式と数の乗法は，数の乗法と同じように，分配法則を使って計算することができる。【Q】の面積は，次のように求めることができる。
ふりかえり
P.48
[mathjax]\( a(b+c)=ab+ac \)
例 ８
⑴
⑵
問 ９ 次の計算をしなさい。
⑴ [mathjax]\(5(x+2)\)
⑵ [mathjax]\(-2(4x+5)\)
⑶ [mathjax]\((1-6x) \times 3\)
⑷ [mathjax]\((a-4) \times (-6)\)
⑸ [mathjax]\(-(-9x+8)\)
⑹ [mathjax]\(\dfrac{2}{3}(9y+6)\)
例 ９
[mathjax]\(\dfrac{(x-5) \times \bcancel{6}^{3}}{_{1}\bcancel{2}} = (x-5) \times 3\)
問 10 次の計算をしなさい。
⑴ [mathjax]\(\dfrac{3x+1}{2} \times 4\)
⑵ [mathjax]\(12 \times \dfrac{x-3}{4}\)
<1年p.84>
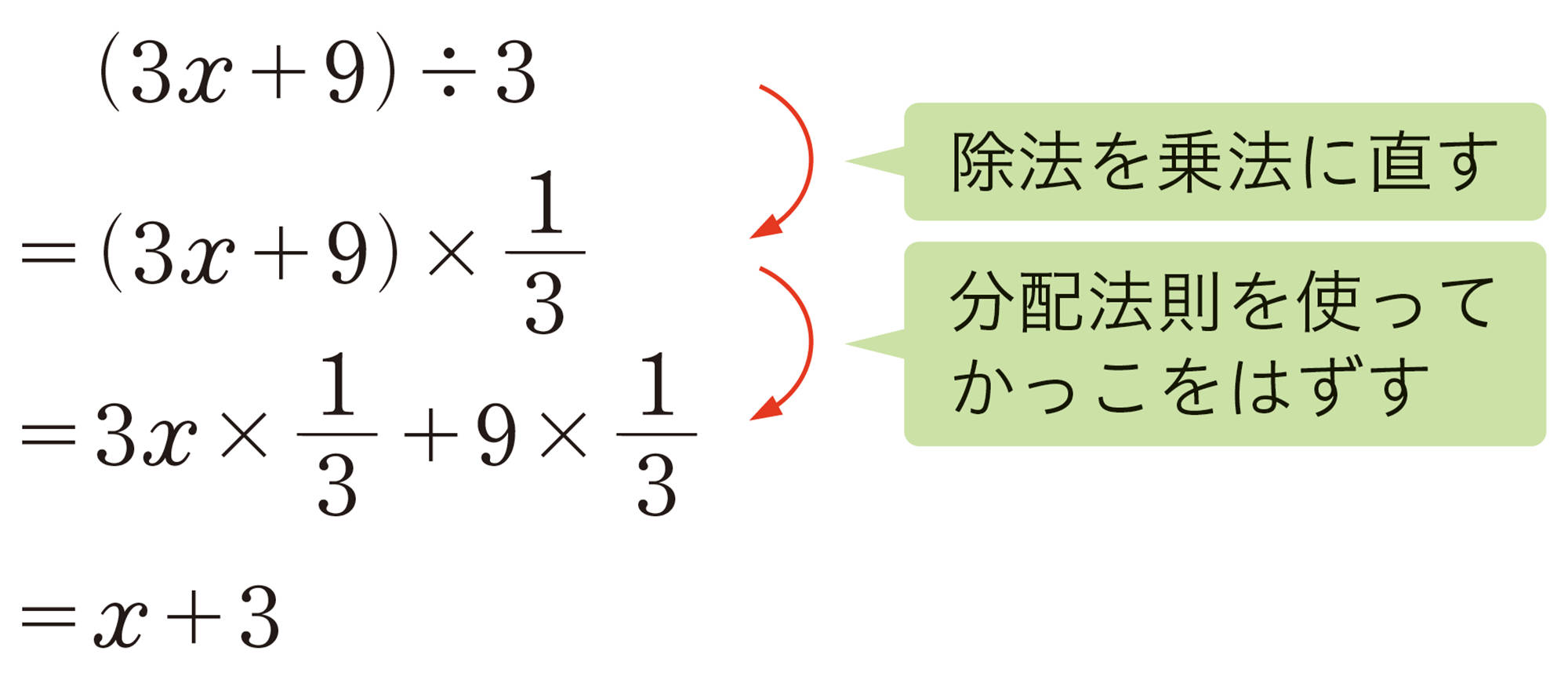
例 10
除法を乗法に直す
分配法則を使ってかっこをはずす
問 11 次の計算をしなさい。
⑴ [mathjax]\((2x+6) \div 2\)
⑵ [mathjax]\((12a-8) \div (-4)\)
⑶ [mathjax]\((10x-5) \div \dfrac{5}{2}\)
問 12 真央さんは，[mathjax]\((8x-3) \div 2\)の計算を，右のように，分数の形に直して行いました。この計算は正しいですか。誤りがあれば，正しく直しなさい。
やってみよう
計算力を高めよう3-3
P.89
いろいろな計算
例 11
⑴
⑵
問 13 次の計算をしなさい。
⑴ [mathjax]\((6x+1)+3(x+2)\)
⑵ [mathjax]\(2(-a+6)+4(a-3)\)
⑶ [mathjax]\(-3(3x-5)+7(2x-1)\)
⑷ [mathjax]\(2(a+5)-8(a+1)\)
⑸ [mathjax]\(6(x-2)-2(3x-7)\)
⑹ [mathjax]\(-(a-8)-5(-2a+4)\)
問 14 次の計算をしなさい。
⑴ [mathjax]\(\dfrac{1}{2}(6x+4) + \dfrac{1}{3}(6x-3)\)
⑵ [mathjax]\(\dfrac{2}{3}(9a-6)- \dfrac{1}{2}(2a-10)\)
やってみよう
計算力を高めよう3-4
P.89
どんなことがわかったかな
1 次式の計算は，これまでの数の計算と同じように分配法則を使って計算することができます。
次の課題へ！
これまでに学んだことを使って，[mathjax] \(66\)，[mathjax] \(67\)ページのストローの問題が解決できるかな？
P.85
