<1年p.71>
2 文字式の表し方
目標 ▷ 文字式の積や商の表し方にしたがって表そう。
積の表し方
[mathjax] \(3 \times a\)や[mathjax] \(a\times 3\)のような文字式の乗法では,[mathjax] \(\times\)の記号を省いて[mathjax] \(3a\)と表す。したがって,68ページの[mathjax] \(1+3\times a\)は,[mathjax] \(1+3a\)と表すことができる。
文字式の積は,次のように表すことができる。
積の表し方
❶ 文字式では,乗法の記号×を省く。
❷ 数と文字の積では,数を文字の前に書く。
例 1
⑴ [mathjax] \(5\times a=5a\)
⑵ [mathjax] \(x\times (-4)=-4x\)
⑶ [mathjax] \(b\times a=ab\)
⑷ [mathjax] \(x\times 6\times y=6xy\)
⑸ [mathjax] \((x+y)\times 2=2(x+y)\)
⑹ [mathjax] \(10-a\times 2=10-2a\)
注意 [mathjax] \(b\times a\)のような文字どうしの積では,ふつう,アルファベット順にして,[mathjax] \(ab\)と表す。
問 1 次の式を,文字式の表し方にしたがって表しなさい。
⑴ [mathjax] \(12 \times x\)
⑵ [mathjax] \(a\times 7\)
⑶ [mathjax] \((-5) \times a\)
⑷ [mathjax] \(y \times \dfrac{2}{3}\)
⑸ [mathjax] \(x \times 0.4\)
⑹ [mathjax] \(y \times 10\times x\)
⑺ [mathjax] \((a-b)\times (-8)\)
⑻ [mathjax] \(x \times 6-3\)
⑼ [mathjax] \(x \times 2+3 \times y\)
[mathjax] \(1 \times a\)は,[mathjax] \(1a\)とはしないで,1を省いて[mathjax] \(a\)と表す。[mathjax] \((-1) \times a\)は,[mathjax] \(-1a\)とはしないで,[mathjax] \(-a\)と表す。ただし,[mathjax] \(0.1 \times a\)は,[mathjax] \(0.a\)とはしないで,[mathjax] \(0.1a\)と表す。
問 2 次の式を,文字式の表し方にしたがって表しなさい。
⑴ [mathjax] \(x \times 1\)
⑵ [mathjax] \(a \times (-1) \times b\)
⑶ [mathjax] \(y \times (-0.1)\)
<1年p.72>
問 3 次の数量を,文字式の表し方にしたがって表しなさい。
⑴ 長さ2m の紙テープx本の長さの合計
⑵ 1個akgの荷物1個と1個bkgの荷物5個の重さの合計
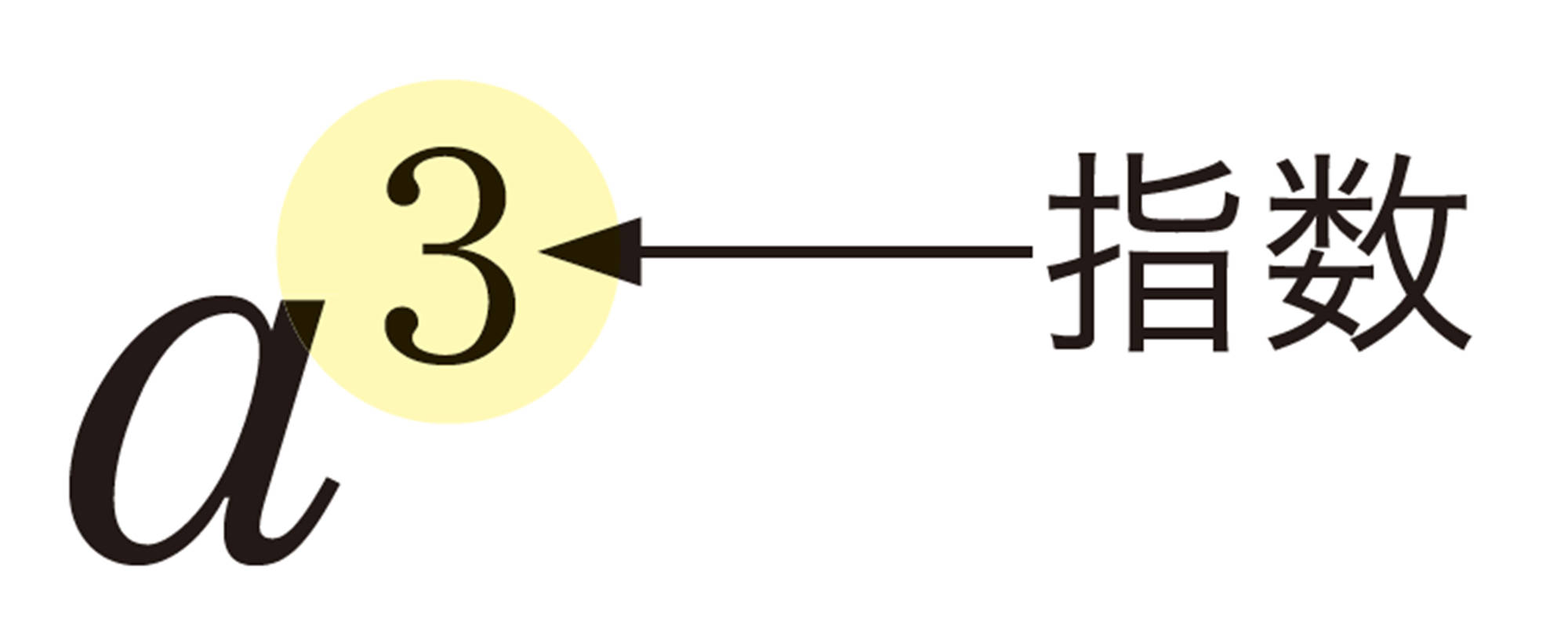
累乗の表し方
Q Question

数では,累乗を指数を使って表したね。
文字も指数を使って表していいのかな。

見方・考え方
数と同じように考えられるかな。
累乗の表し方
同じ文字の積は,累乗の指数を使って表す。
おしえて!
P.77
累乗で,[mathjax] \(a¹\)や[mathjax] \(a⁰\)と表すことはあるのかな?
例 2
⑴ [mathjax]\(x \times x \times 3=3x²\)
⑵ [mathjax]\(a \times (-1) \times a \times a=-a³\)
⑶ [mathjax]\(a \times a \times a \times b \times b=a³b²\)
問 4 次の式を,累乗の指数を使って表しなさい。
⑴ [mathjax]\(a \times 7 \times a\)
⑵ [mathjax]\(x\times x \times (-2)\times x\)
⑶ [mathjax]\(x \times y \times y \times x \times y\)
問 5 次の式を,乗法の記号[mathjax]\(\times\)を使って表しなさい。また,[mathjax]\(a=\dfrac{1}{3}\) のときの式の値を求めなさい。
⑴ [mathjax] \(-12a\)
⑵ [mathjax]\(9a²-2\)
問 6 次の式を,乗法の記号[mathjax]\(\times \)を使って表しなさい。また,[mathjax]\(a=-4\),[mathjax]\(b=2\)のときの式の値を求めなさい。
⑴ [mathjax] \(-a\)
⑵ [mathjax] \(a²\)
⑶ [mathjax]\(3a+5b\)
⑷ [mathjax]\(2a-4b²\)
<1年p.73>
商の表し方
[mathjax]\(a \div 3\)や[mathjax]\(5 \div a\)のような文字式の除法では,[mathjax]\(\div\)の記号を使わずに[mathjax]\(\dfrac{a}{3}\)や[mathjax]\(\dfrac{5}{a}\)と表す。
文字式の商は,次のように表すことができる。
[mathjax]\(a\div 3=\dfrac{a}{3}\)
[mathjax]\(5 \div a = \dfrac{5}{a}\)
商の表し方
文字式では,除法の記号[mathjax]\(\div\)を使わずに,分数の形で表す。
注意 文字でわる場合,その文字は0でないものとする。
例 3
⑴ [mathjax]\(x \div 8=\dfrac{x}{8}\)
⑵ [mathjax]\(6 \div a=\dfrac{6}{a}\)
⑶ [mathjax]\((a+b) \div 2=\dfrac{a+b}{2}\)
⑷ [mathjax]\(x \div (-4)=\dfrac{x}{-4}=-\dfrac{x}{4}\)
注意 [mathjax]\(x \div 8\) は[mathjax]\(x \times \dfrac{1}{8}\)と同じことなので, [mathjax]\(\dfrac{x}{8}\)は[mathjax]\(\dfrac{1}{8}x\)と表すこともある。
同じように,[mathjax]\(\dfrac{a+b}{2}\)は[mathjax]\(\dfrac{1}{2}(a+b)\)と表すこともある。
問 7 次の式を,文字式の表し方にしたがって表しなさい。
⑴ [mathjax]\(x \div 6\)
⑵ [mathjax]\(a \div b\)
⑶ [mathjax]\((x-y) \div 5\)
⑷ [mathjax]\(a \div (-7)\)
問 8 次の式を,除法の記号 [mathjax]\(\div\)を使って表しなさい。また, [mathjax]\(x=-3\), [mathjax]\(y=2\)のときの式の値を求めなさい。
⑴ [mathjax]\(\dfrac{x}{7}\)
⑵ [mathjax]\(\dfrac{x+y}{3}\)
⑶ [mathjax]\(\dfrac{x}{9} – \dfrac{y}{5}\)
問 9 次の数量を,文字式の表し方にしたがって表しなさい。
⑴ 長さam のテープを5等分したときの1本分の長さ
⑵ 面積20 cm²の長方形で,縦がx cmのときの横の長さ
⑶ 3つの荷物の重さが,それぞれa kg,b kg,c kg のとき,これらの荷物の重さの平均
<1年p.74>
いろいろな数量の表し方
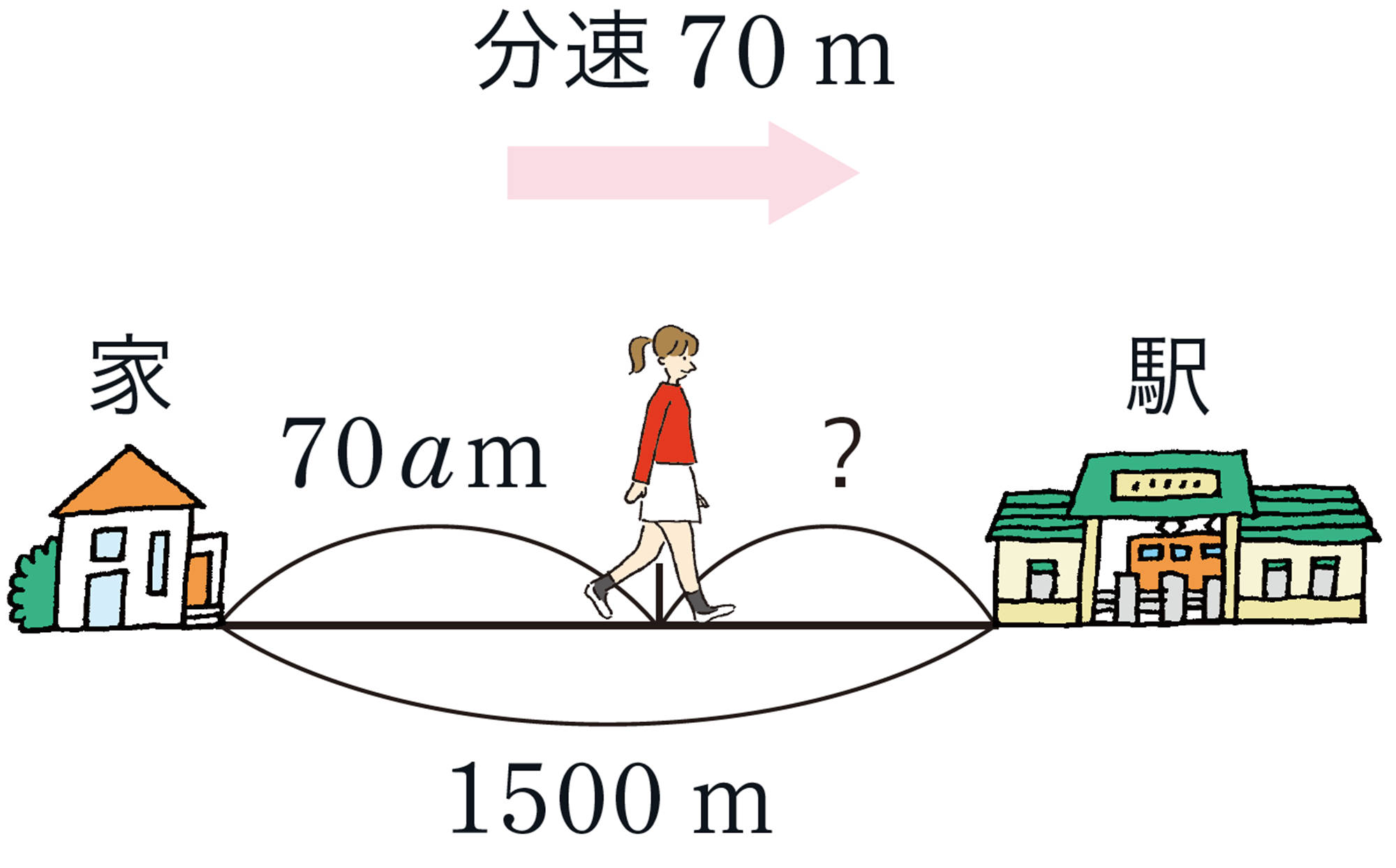
例 4 結菜さんは,家から駅までの1500m の道のりを,分速70m で歩いています。結菜さんが家を出発してからa分間歩いたとき,駅までの残りの道のりは何 mですか。
ふりかえり
小学校5年
[mathjax]\(\text{(速さ)}=\text{(道のり)} \div \text{(時間 )}\)
[mathjax]\(\text{(道のり)}=\text{(速さ )}\times\text{(時間 )}\)
[mathjax]\(\text{(時間 )}=\text{(道のり)}\div \text{(速さ)}\)
考え方 全体の道のりから, 歩いた道のりをひいたものが,残りの道のりになる。
速さ,道のり,時間の関係は,小学校で学んだね。

解答
問 10 例4で,12分間歩いたとき,駅までの残りの道のりを求めなさい。
問 11 次の数量を,文字式で表しなさい。
⑴ 分速60 mでa分間歩いたときの道のり
⑵ x km の道のりを時速4 km で歩いたときにかかる時間
⑶ 1200 m の道のりをa分間で歩いたときの速さ
⑷ 自動車に乗って140 km の道のりを走るとき,時速x kmで2時間走ったときの残りの道のり
例 5 音が空気中を伝わる速さは,気温によって変化する。気温がt℃のときの音の速さは,[mathjax] \((331.5+0.6t)\)m/sという式で表すことができる。
気温が[mathjax] \(-5\)℃のときの音の速さは,上の式に [mathjax] \(t=-5\) を代入して,
[mathjax] \(331.5+0.6 \times (-5)=328.5\)
より,[mathjax]\(328.5\)m/sとなる。
気温が上がると,音の速さは速くなるんだね。

<1年p.75>
解答
分数は2行使って書こう。
31%を分数で表すと,[mathjax] \(\dfrac{31}{100}\) である。
したがって, x 人の31 %は,
[mathjax] \( x\times \dfrac{31}{100}=\dfrac{31}{100} x\)
答 [mathjax] \(\dfrac{31}{100} x\) 人
割合を小数で表すと,人数はどう表せるかな。

問 13 例6で,総入場者数が1400人のとき,水族館を訪れた子どもは何人ですか。
問 14 次の数量を文字式で表しなさい。
⑴ xg の12%
⑵ y円の8%
⑶ a人の3割
問 15 次の問いに答えなさい。
⑴ 令和4年の国内での米の収穫量第1位は新潟県で,全収穫量の約[mathjax]\(8.7\) %でした。全収穫量をxt としたとき,新潟県の米の収穫量は約何t ですか。
⑵ ある店で,定価の2割引きセールを行っています。このとき,定価a円の品物はいくらで買うことができますか。
⑶ ある中学校の昨年度の生徒数はx人で,今年度は昨年度に比べ生徒数が3%増えました。今年度の生徒数は何人ですか。
<1年p.76>
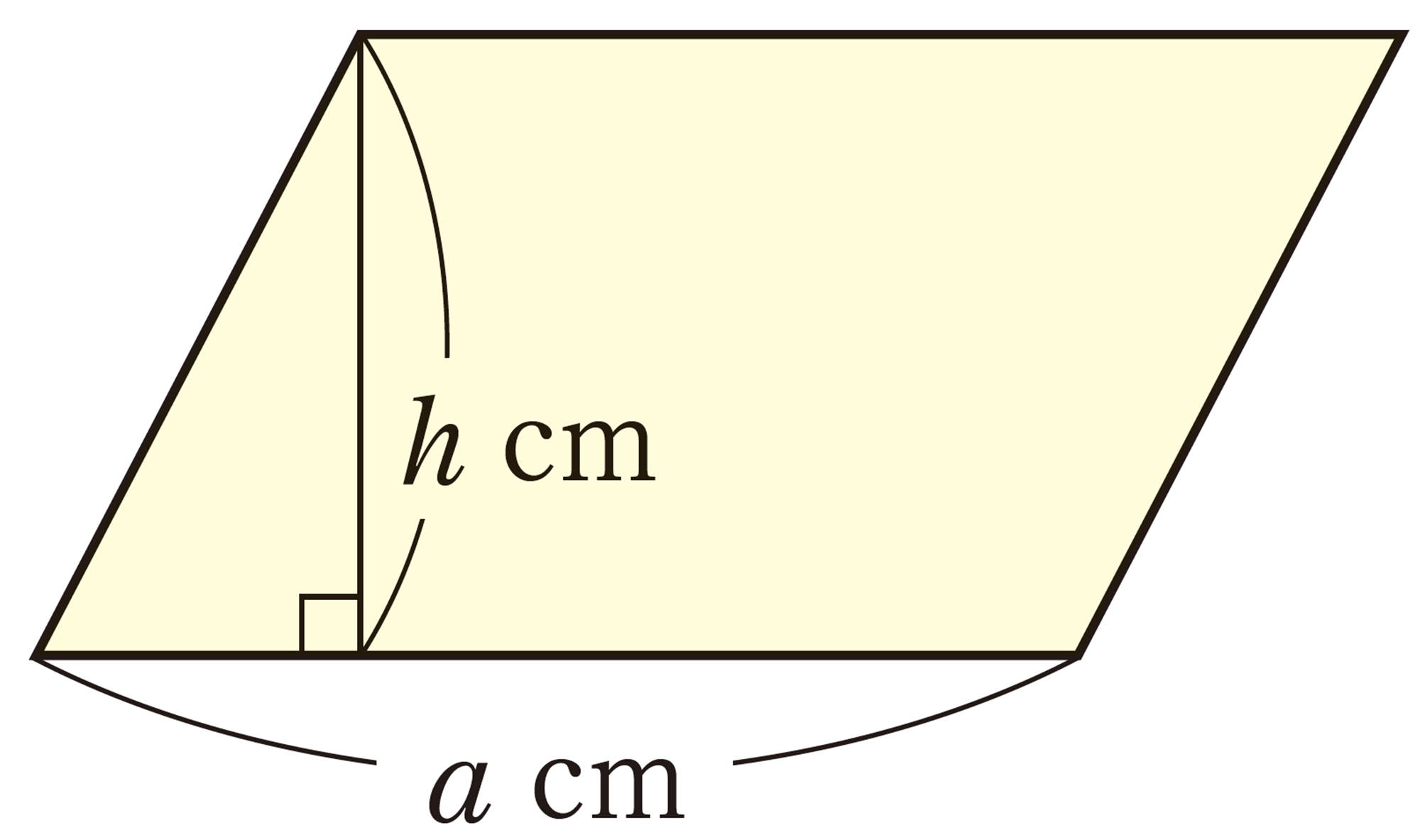
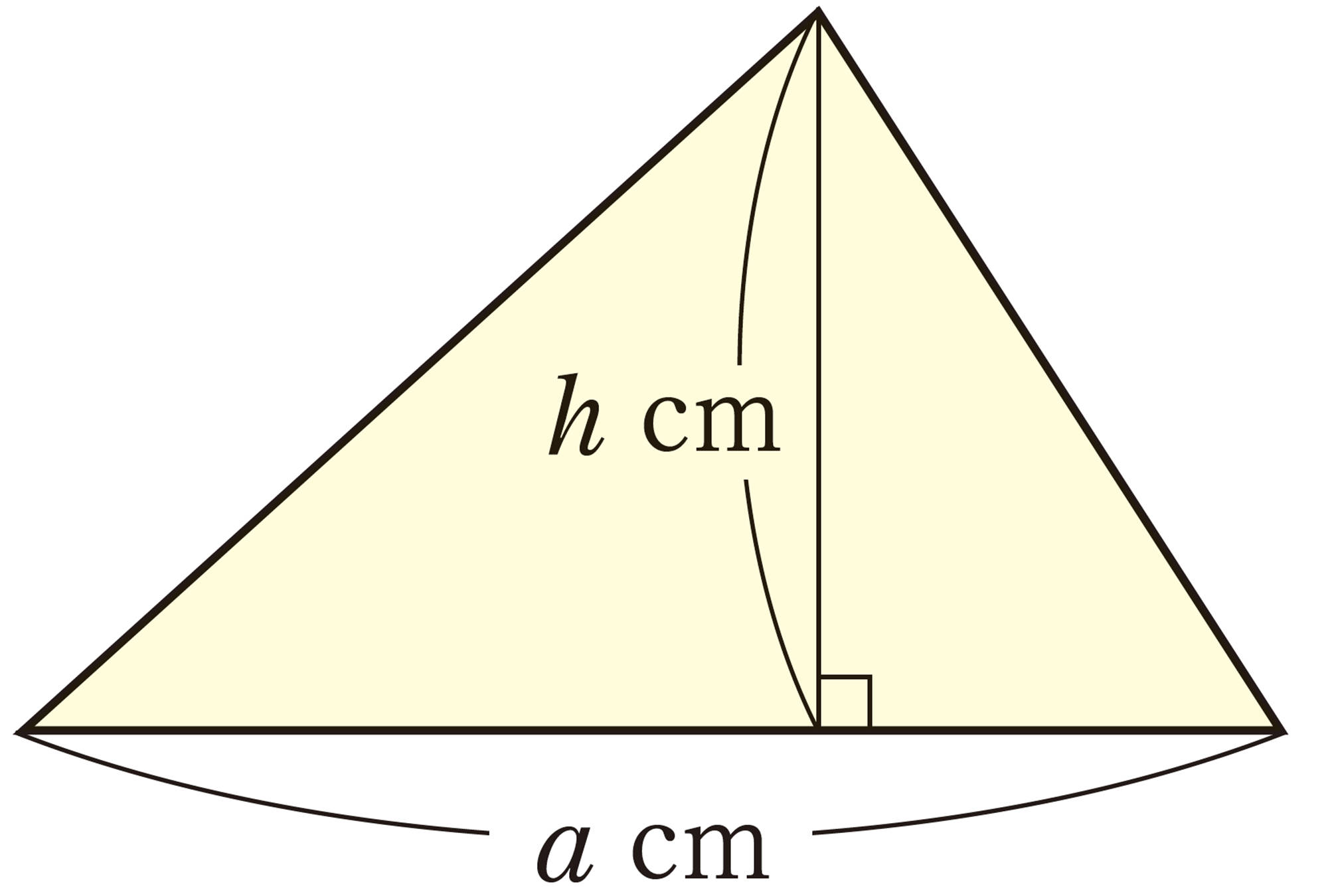
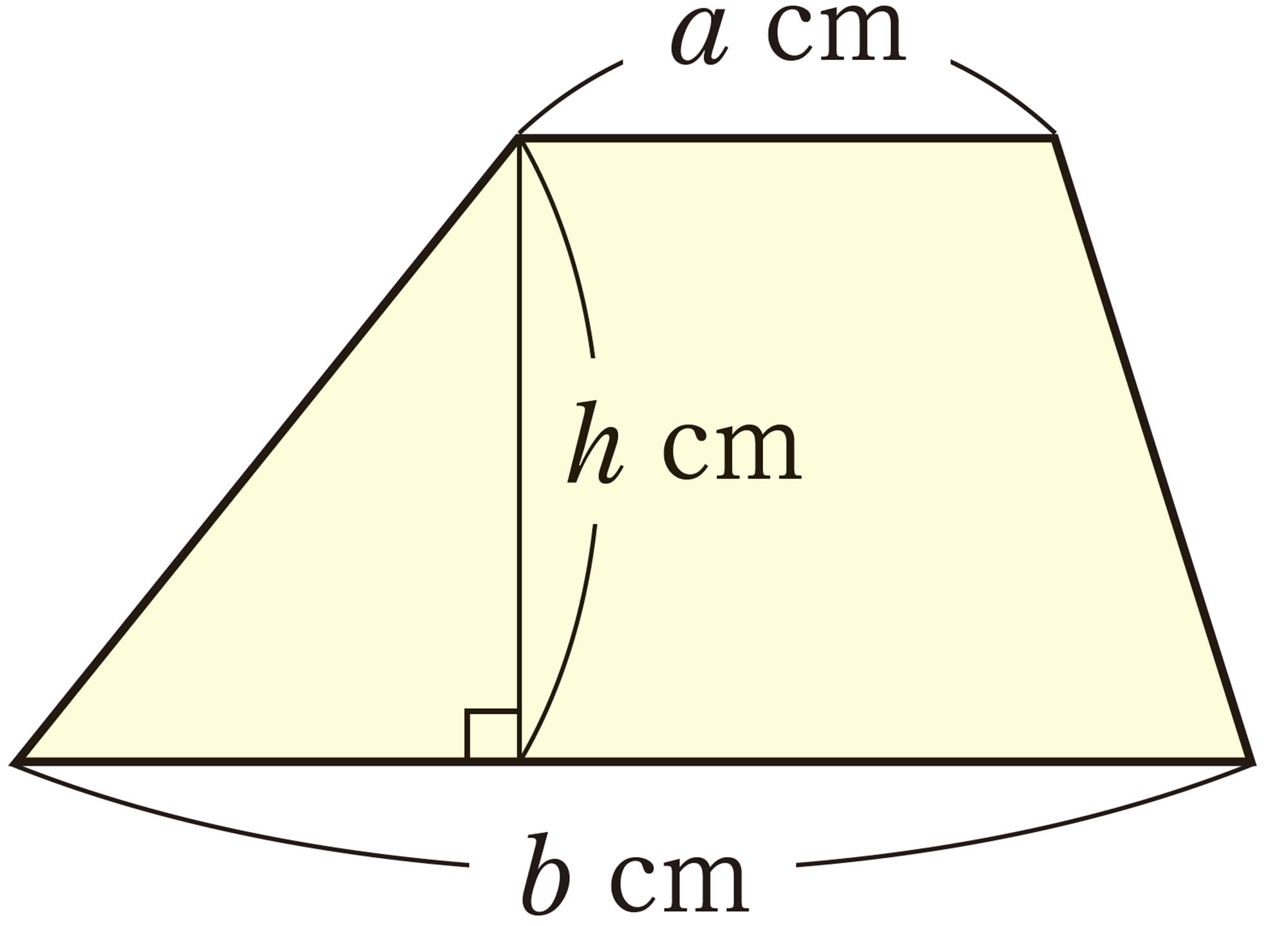
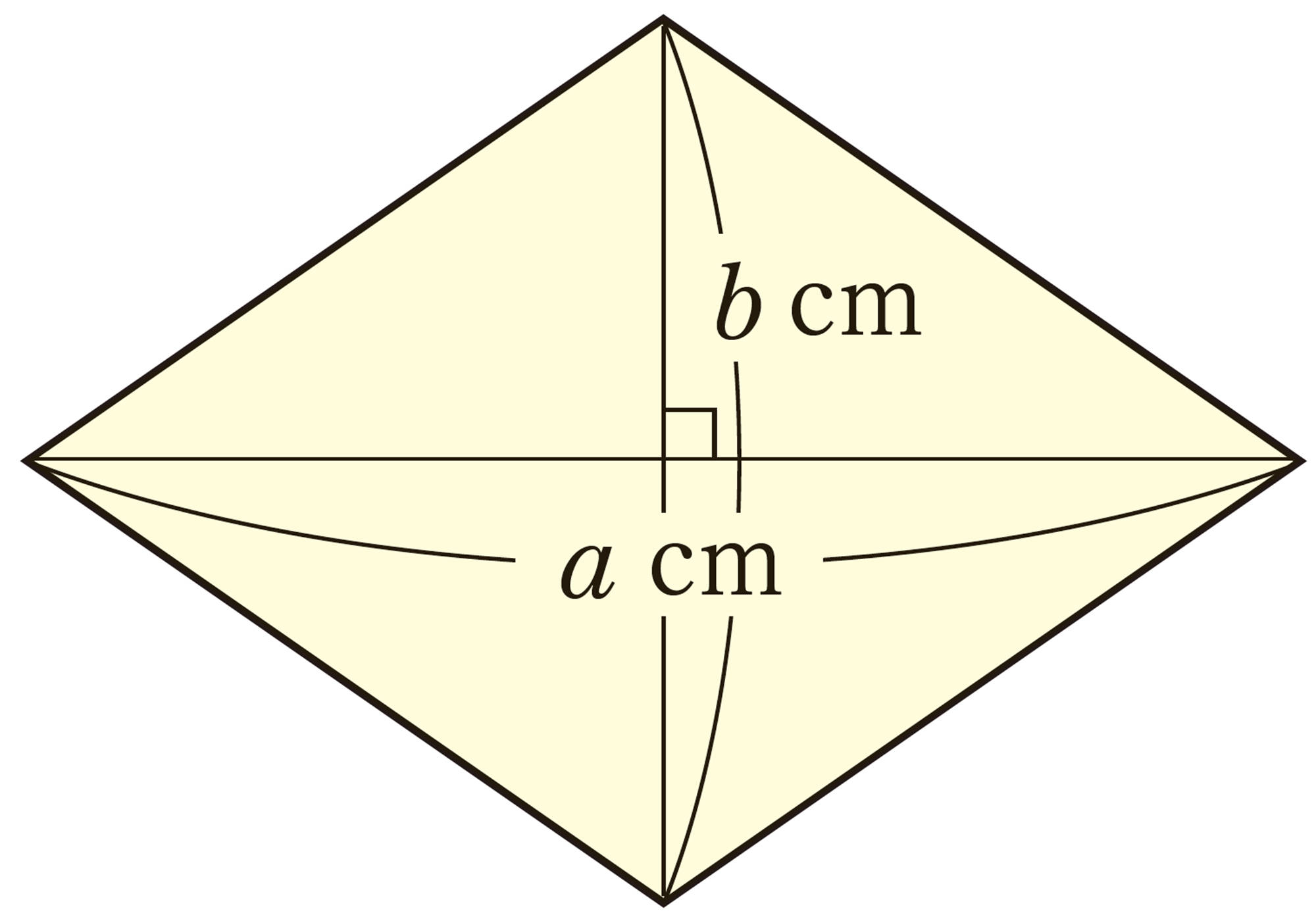
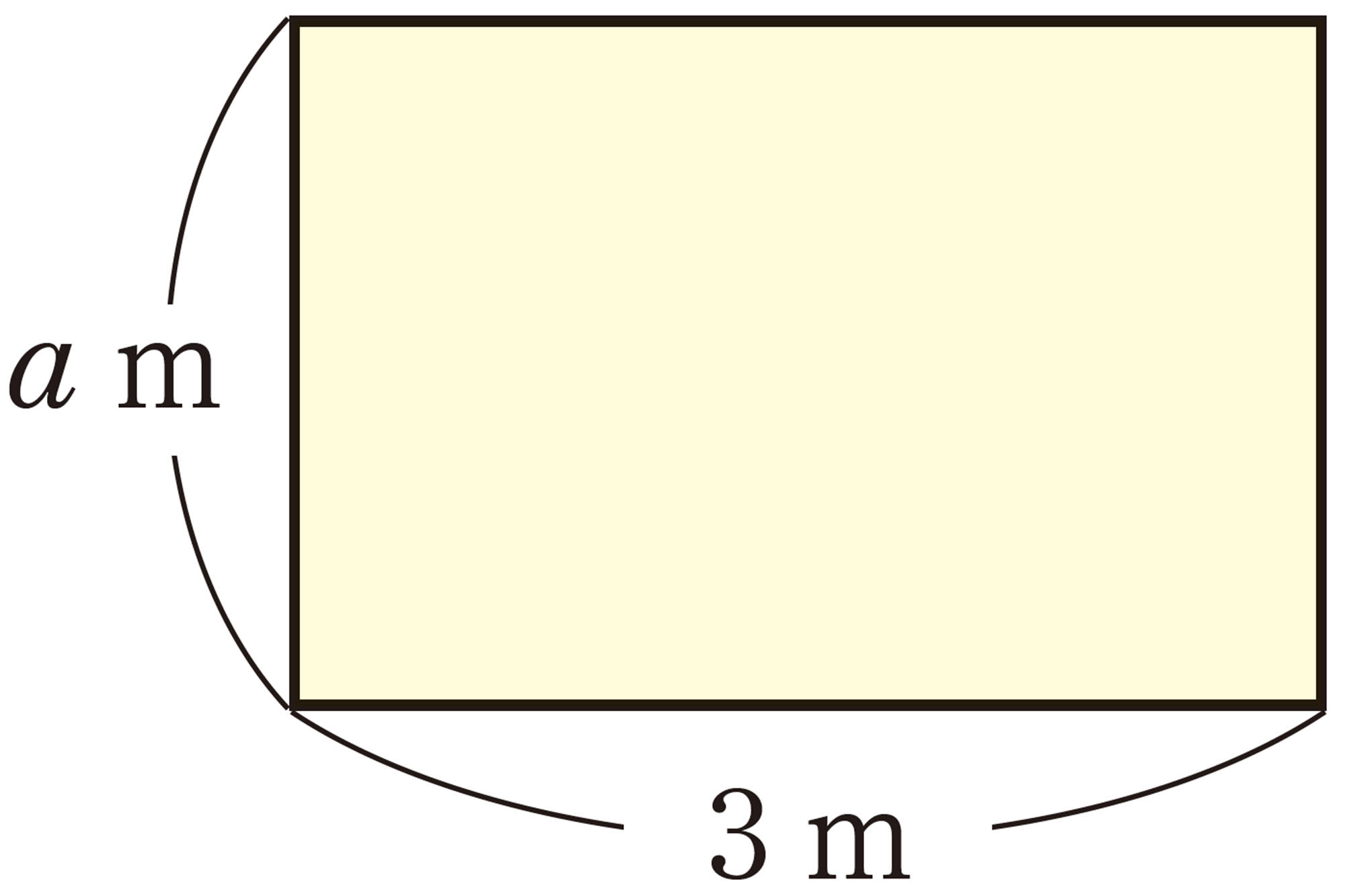
問 16 次の図形の面積を,文字式で表しなさい。
式の表す数量
問 17 例8で,5x円,[mathjax] \((x+14y)\)円,[mathjax] \((x-y)\)円は,それぞれどんな数量を表していますか。
<1年p.77 >
問 18 家から図書館までの道のりのうち,はじめのa m は分速250 m で自転車で走り,残りのb m は分速40 m で歩きました。このとき,次の式はどんな数量を表していますか。また,その単位をいいなさい。
⑴ [mathjax]\(a+b\)
⑵ [mathjax]\(\dfrac{a}{250}+ \dfrac{b}{40}\)
⑴ 3a
⑵ [mathjax]\(2a+6\)
⑶ [mathjax]\(a+a+3+3\)
どんなことがわかったかな
文字式では,積の記号[mathjax]\(\times\)を省略して表したり,商の記号[mathjax]\(\div\)を使わずに分数の形で表したりすることができます。
次の課題へ!
問19⑵と⑶は,同じ数量を表しているのに式がちがうね。2つの式が同じものだと説明できるのかな?
P.79

[mathjax] \(a¹\) や[mathjax] \(a⁰\)はあるのかな? 発展 高等学校 Tea Break
[mathjax]\(a \times a=a²\),[mathjax]\(a \times a \times a=a³\)のように,同じ文字の積は,累乗の指数を使って表すことができます。では,[mathjax] \(a¹\)や[mathjax] \(a⁰\)のように,指数に1や0を使うことはあるのでしょうか。ただし,[mathjax]\(a \neq 0\)とします。
右の図のように,指数が1増えるということは,aを1つかけていることと同じです。したがって,指数が1減るということは, aでわることと同じ意味になります。
つまり,[mathjax] \(a¹\)はa,[mathjax] \(a⁰\)は1と考えます。
![]() [mathjax] \(a⁻¹\)のように累乗の指数が[mathjax] \(-1\)のとき,どんな数を表しているか考えてみましょう。
[mathjax] \(a⁻¹\)のように累乗の指数が[mathjax] \(-1\)のとき,どんな数を表しているか考えてみましょう。
<1年p.78 >
確かめよう 1節 文字式
⑴ [mathjax]\(x\times 5\)
⑵ [mathjax]\(\require{physics} \left(-\dfrac{1}{4}\right) \times a\)
⑶ [mathjax]\((x-y) \times 6\)
⑷ [mathjax]\((-1) \times x \times y\)
⑸ [mathjax]\(y \times 4 \times y\)
⑹ [mathjax]\(2\times x+y \times 8\)
⑺ [mathjax]\(a \div 9\)
⑻ [mathjax]\((a+b)\div 5\)
2 次の数量を,文字式で表しなさい。
⑴ 1個5 kg の荷物a個の重さ
⑵ xL の水を,3人で等分したときの1人分の水の量
⑶ a人の班が4つとb人の班が7つあるときの人数の合計
⑷ 分速70 m でx分間歩いたときの道のり
⑸ 全校生徒x人の47 % が女子であるときの女子の人数
□ 式の値を求めることができる。 文字式の表し方P.72問5
⑴ [mathjax] \(-4a\)
⑵ [mathjax]\(a²-2\)
⑶ [mathjax]\(5a+1\)
□ 文字式が表している数量を読み取ることができる。 式の表す数量P.76例8