<1年p.54>
4節 数の集合
数の範囲と計算の関係は？
負の数を学んで，0と正の数だけではできなかった計算ができるようになりました。数の範囲と計算について考えてみましょう。
【１】 次の[mathjax]\(\boxed{\phantom{00}}\)にどんな自然数を入れても，計算の結果がいつでも自然数になるといえるでしょうか。
㋐ [mathjax]\(\boxed{\phantom{00}}+\boxed{\phantom{00}}\)
㋑ [mathjax]\(\boxed{\phantom{00}}-\boxed{\phantom{00}}\)
㋒ [mathjax]\(\boxed{\phantom{00}}\times \boxed{\phantom{00}}\)
㋓ [mathjax]\(\boxed{\phantom{00}}\div\boxed{\phantom{00}}\)
自然数だけだと，できない計算があるね。
負の数をふくめると，四則の計算が全部できるのかな。
次の課題へ！
負の数を学んで，計算できる範囲が広がったのかな？
P.54
１ 数の集合と四則
目標 ▷ これまでに学んできた数と計算の関係についてまとめよう。
【１】からわかるように，数の範囲を自然数全体の集まりと考えると，加法や乗法の計算の結果はいつでも自然数にふくまれる。つまり，加法や乗法はいつでもできる。一方，減法や除法の計算の結果は自然数にふくまれない場合がある。つまり，減法や除法はできない場合がある。
このように数の範囲を「自然数全体」や「整数全体」など，ある条件にあてはまるものをひとまとまりにして考えるとき，そのまとまりを 集合 という。
<1年p.55>
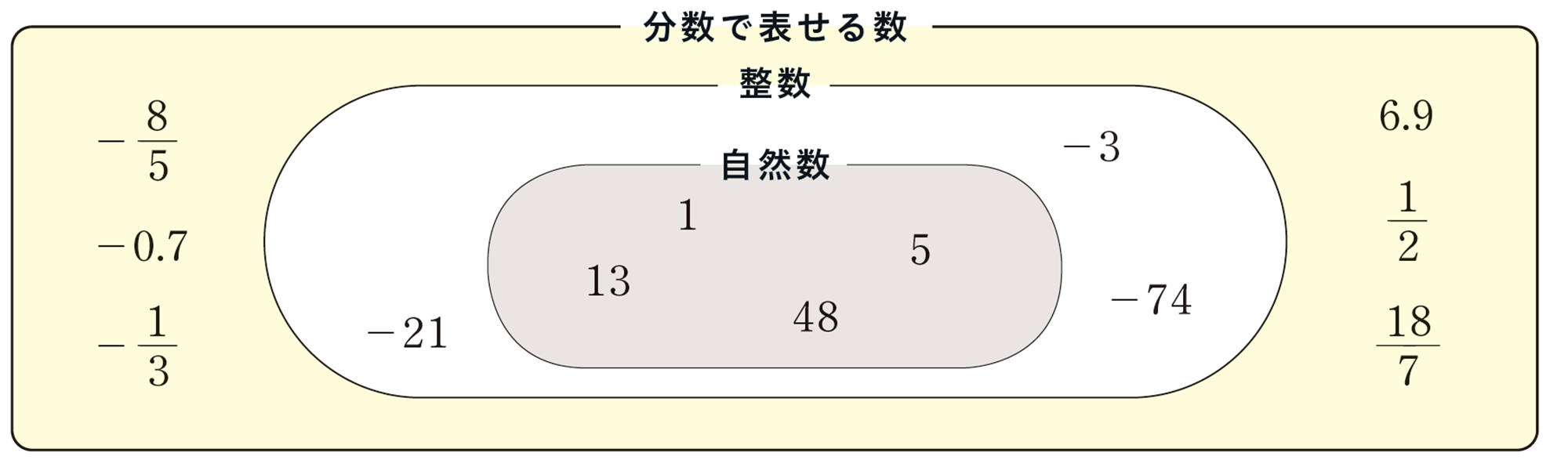
自然数は正の整数であるから，自然数の集合は，整数の集合にふくまれる。また，整数の集合は，分数や小数をふくんだ，分数で表せる数の集合にふくまれる。
自然数の集合，整数の集合，分数で表せる数の集合の関係は，前ページのような図で表すことができる。
問 １ 次の数は，数の集合の図で，どの部分に入りますか。前ページの図に，それぞれ書き入れなさい。
[mathjax] \(-16\)，[mathjax] \(92\)，[mathjax] \(1000\)，[mathjax] \(0.3\)，[mathjax]\(-\dfrac{1}{60}\)，[mathjax] \(0\)
問 ２ 次の表で，数の範囲を左側にあげた数の集合として四則を考えます。計算がいつでもできるものには〇，できない場合があるものには×を書き入れなさい。また，×の場合には，計算ができない例を1つ示しなさい。ただし，除法では，0でわることは除いて考えるものとします。
自然数の集合では，加法と乗法の計算はいつでもできる。数の集合を整数の集合にまで広げると，加法と乗法のほかに，減法もいつでもできるようになる。さらに，数の集合を分数で表せる数の集合にまで広げると，0でわることを除いた四則がいつでもできるようになる。
このように，数の集合は，四則が自由にできるように広げられてきたと考えることができる。
どんなことがわかったかな
数の集合は，四則が自由にできるように，数の範囲が広げられてきたと考えることができます。
次の課題へ！
数の集合には，ほかにどんなものがあるのかな？
P.56
<1年p.56>
２ 素数
目標 ▷ 自然数について，数の集合にはどんなものがあるか調べよう。
Q Question
偶数や奇数は，それぞれどのような数の集合でしょうか。ほかには，どのような数の集合が考えられるでしょうか。話し合ってみましょう。
2でわり切れる数とわり切れない数だね。
倍数や約数の集まりも，数の集合といえるのかな。
見方・考え方
どんな分類ができるかな。
例 １ 数の集合には，たとえば，次のようなものが考えられます。
⑴ 10以下の自然数の集合
⑵ 1から20までの奇数の集合
⑶ 10の約数の集合
⑷ 5の倍数の集合
素数
問 １ 1から10までの自然数のうち，次の条件にあてはまる数をいいなさい。
⑴ 約数が1つだけの数
⑵ 約数が2つだけある数
⑶ 約数が3つだけある数
⑷ 約数が4つある数
7の約数は，1と7の2つだけである。このように，1とその数自身のほかには約数のない自然数を 素数 という。ただし，1は素数にふくめない。したがって，素数の集合は約数を2つだけもつ自然数の集まりである。
問 ２ 1から20までの自然数のうち，素数をすべていいなさい。
素因数分解
Q Question
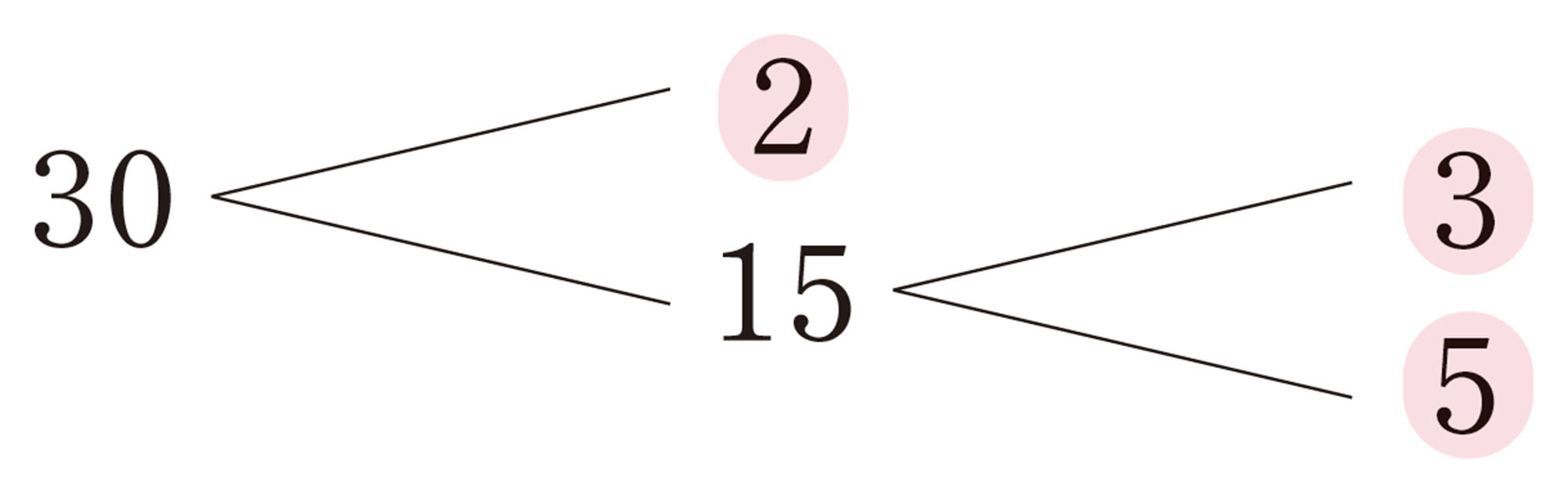
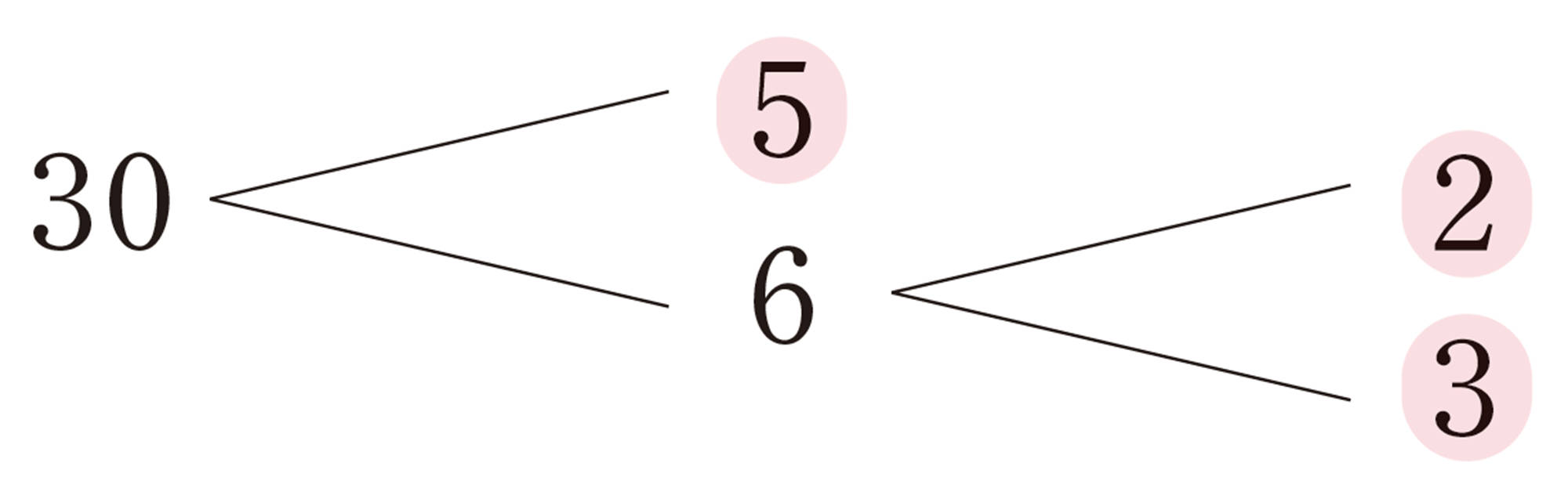
30をいくつかの自然数の積で表してみましょう。どんな表し方があるでしょうか。
30の約数を考えればいいね。
2つの数の積で表せるね。3つの数の積でも表せるかな。
見方・考え方
どんな表し方ができるかな。
<1年p.57>
1と素数を除く自然数は，[mathjax] \( 30=2 \times 3 \times 5\)のように，素数の積で表すことができる。30の約数[mathjax] \(2\)，[mathjax] \(3\)，[mathjax] \(5\)のように，素数である約数を，もとの自然数の 素因数 といい，自然数を素因数だけの積で表すことを，その数を 素因数分解 するという。
素因数分解は，どんな順序で行っても同じ結果になる。
例 ２ 150を素因数分解しなさい。
考え方 右のように，素数で順にわっていき，商が素数になるまで続ける。
解答
答 [mathjax] \( 2\times 3\times 5²\)
問 ３ 次の数を素因数分解しなさい。
⑴ 24
⑵ 32
⑶ 75
⑷ 132
問 ４ ある自然数を2乗すると，1764になります。この自然数を求めなさい。
素因数分解の利用
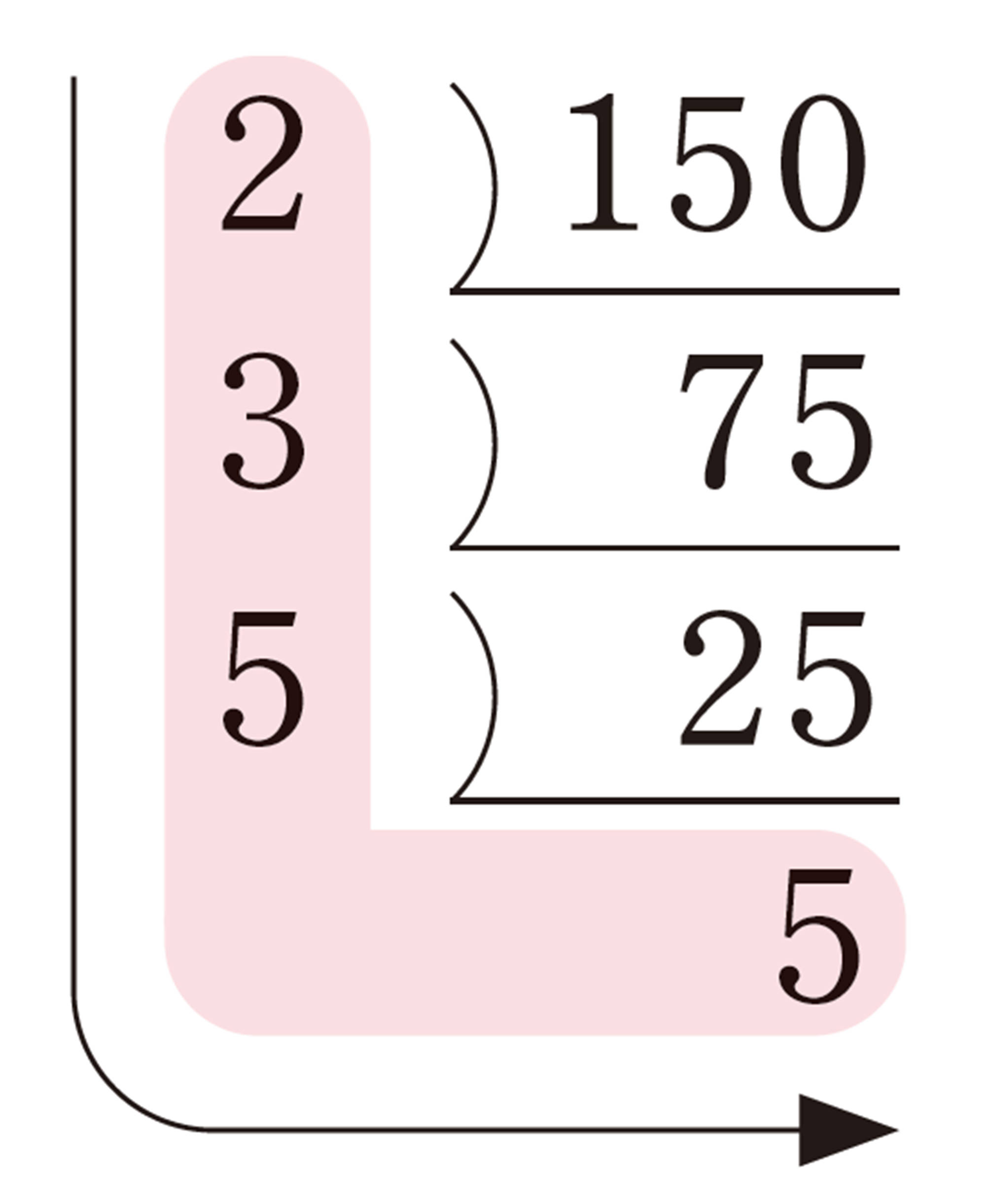
例 ３ 75の約数をすべて求めなさい。
解答
75 を素因数分解すると，
[mathjax]\(75=3\times 5²\)
3 の約数は[mathjax] \(1\)，[mathjax] \( 3\) で，[mathjax] \(5²\) の約数は[mathjax] \(1\)， [mathjax] \(5\)，[mathjax] \( 5²\) である。
右の図のように考えると，75 の約数は， [mathjax] \(1\)， [mathjax] \(3\)， [mathjax] \(5\)， [mathjax] \(15\)， [mathjax] \(25\)，[mathjax] \(75\) である。
答 [mathjax] \(1\)， [mathjax] \(3\)，[mathjax] \(5\)， [mathjax] \(15\)， [mathjax] \(25\)， [mathjax] \(75\)
問 ５ 次の数を素因数分解して，約数をすべて求めなさい。
⑴ 45
⑵ 36
<1年p.58>
例 ４ 36と90の最大公約数を求めなさい。
解答
36 と90 をそれぞれ素因数分解すると，
[mathjax]\(36=2²\times 3² \)
[mathjax] \(90=2\times 3² \times 5\)
したがって， 最大公約数は，
[mathjax]\(2\times 3² = 18\)
答 18
ふりかえり ▷小学校5年
2つの数の約数に共通な数を，その2つの数の公約数という。
最大公約数を求めるには，例4のように，それぞれの数を素因数分解して，共通な素因数の積をつくればよい。
問 ６ 次の各組の数の最大公約数を求めなさい。
⑴ [mathjax] \(60\)，[mathjax] \(80\)
⑵ [mathjax] \(72\)，[mathjax] \(96\)
⑶ [mathjax] \(80\)，[mathjax] \(216\)
問 ７ [mathjax] \(84\)，[mathjax] \(120\)をわり切れる自然数のうちで，もっとも大きい自然数を求めなさい。
例 ５ 36と90の最小公倍数を求めなさい。
解答
36 と90 をそれぞれ素因数分解すると，
[mathjax]\(36=2²\times 3²\)
[mathjax] \(90=2\times 3² \times 5\)
したがって， 最小公倍数は，
[mathjax] \( 2²\times 3² \times 5=180\)
答 180
ふりかえり▷小学校5年
2つの数の倍数に共通な数を，その2つの数の公倍数という。
最小公倍数を求めるには，例5のように，それぞれの数を素因数分解して，共通な素因数と残りの素因数との積をつくればよい。
問 ８ 次の各組の数の最小公倍数を求めなさい。
⑴ [mathjax] \(16\)，[mathjax] \(24\)
⑵ [mathjax] \(42\)，[mathjax] \(54\)
⑶ [mathjax] \(12\)，[mathjax] \(21\)
問 ９ 30でわっても，75でわってもわり切れる自然数のうちで，もっとも小さい自然数を求めなさい。
どんなことがわかったかな
自然数の中には素数があり，素因数分解を利用すると，最大公約数や最小公倍数を求めることができます。
<1年p.59>
確かめよう 4節 数の集合
□ 数の集合と四則の関係について理解している。 数の集合と四則 P.55問2
１ 四則の中で，自然数の集合でいつでも計算できるものをいいなさい。また，整数の集合でいつでも計算できるものをいいなさい。
２ 次の数で，素数はどれですか。
[mathjax] \(2\)，[mathjax] \(4\)，[mathjax] \(9\)，[mathjax] \(11\)，[mathjax] \(51\)，[mathjax] \(89\)
□ 素因数分解をすることができる。 素因数分解 P.57例2
３ 次の数を素因数分解しなさい。
⑴ 40
⑵ 84
⑶ 144
□ 素因数分解を利用して，2数の最大公約数を求めることができる。 素因数分解の利用 P.58例4
４ 次の各組の数の最大公約数を求めなさい。
⑴ [mathjax] \(36\)，[mathjax] \(42\)
⑵ [mathjax]\(2³ \times 3²\)，[mathjax]\(2² \times 3³\)
□ 素因数分解を利用して，2数の最小公倍数を求めることができる。 素因数分解の利用 P.58例5
５ 次の各組の数の最小公倍数を求めなさい。
⑴ [mathjax] \(60\)，[mathjax] \(84\)
⑵ [mathjax]\(2² \times 3\)，[mathjax]\(2 \times 3 \times 5\)
素数の話 Tea Break
次のような方法で，100以下の素数を求めてみましょう。
右の図のように自然数を書き並べ，まず1を消す。次に2を残して2の倍数を消す。さらに3を残して3の倍数を消す。このようにして，残った数のうち，最初にあるものを残して，その倍数を次々に消していくと，[mathjax] \(2\)，[mathjax] \(3\)，[mathjax] \(5\)，[mathjax] \(7\)，[mathjax] \(11\)，…というように，25個の素数だけが残る。
このような方法は，古代ギリシャのエラトステネス（紀元前275頃〜紀元前194頃）に由来するので，エラトステネスの篩と呼ばれています。右の図は，エラトステネスの篩をもとにくふうしたものです。
<1年p.60>
1章 「正の数・負の数」を学んで
できるようになったこと 身のまわりの課題へ ▷P.63,64
正の数と負の数について，大小を比べたり，数直線に表したりすることができる。
正の数と負の数の計算を，小学校で学んだ計算と同じようにできる。
身のまわりや数学の中から見つけた問題を，正の数，負の数を使って，解決することができる。
さらに学んでみたいこと
これからもっと学んでみたいことや，疑問に思ったことを書いておこう。
数学へのいざない RSA暗号
現在の社会はコンピュータ社会と呼ばれ，ネット上にクレジットカードや銀行口座の番号など個人情報が飛び交っています。そこで，このような個人情報を暗号化し，安全性を確保する必要があります。
現在，インターネットで広く使われている公開鍵暗号の代表的なものの1つに「RSA暗号」があります。RSA暗号は，暗号化する鍵を公開しても，簡単には解読できません。その理由は，素因数分解に関係しています。桁数が大きくなっても2数の積は簡単に求められますが，桁数が大きい数を素因数分解するのは，コンピュータを使っても長い時間がかかる，という性質を使っています。そこで，RSA暗号では，桁数の大きい2つの素数の積を，暗号をつくるための鍵として公開し，もとの2つの素数を，暗号をもとにもどすための秘密の鍵として使っています。このように，素因数分解の難しさが，RSA暗号の安全性を支えています。
関連 裏見返し
