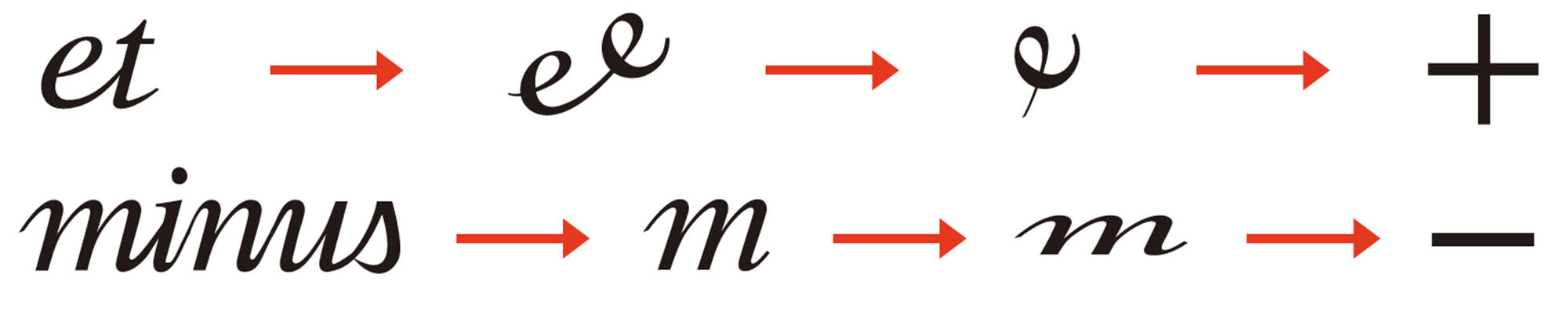<1年p.47>
３ 四則の混じった計算
Q Question
真央さんは，[mathjax]\(25+(-2)\times 10\)の計算を次のように行いました。この計算は正しいでしょうか。また，その理由を説明してみましょう。
正しいかな？
見方・考え方
小学校で学んだ計算の順序と同じように考えられるかな。
小学校のときに，加法や減法より乗法や除法を先に計算したね。
負の数があっても，乗法や除法を先に計算するのかな。
目標 ▷ 四則の混じった計算を考えよう。
例 １
加法，減法と乗法，除法が混じっているときは，乗法，除法を先に計算する。
問 １ 次の計算をしなさい。
⑴ [mathjax]\(-7+(-3) \times 2\)
⑵ [mathjax]\(8+(-20) \div (-4)\)
⑶ [mathjax]\(14-10 \times (-3)\)
⑷ [mathjax]\((-6) \times (-5)-(-18)\div 6\)
例 ２
かっこがあるときは，かっこの中を先に計算する。
問 ２ 次の計算をしなさい。
⑴ [mathjax]\((7-19) \div 3\)
⑵ [mathjax]\((-2)\times (4-9)\)
⑶ [mathjax]\(21 \div (-2-5)\)
⑷ [mathjax]\(\{6-(-3)\} \times 8\)
例 ３
累乗があるときは，累乗を先に計算する。
<1年p.48>
問 ３ 次の計算をしなさい。
⑴ [mathjax]\(12 \div (-2)²\)
⑵ [mathjax]\(-3² + 10\)
⑶ [mathjax]\(6-(-4)²\)
⑷ [mathjax]\((-6)²+(-7²)\)
問 ４ 次の計算をしなさい。
⑴ [mathjax]\(4+7 \times (6-7)\)
⑵ [mathjax]\(10-(-8+5) \times 6\)
⑶ [mathjax]\(5-(6-2³) \times (-3)\)
⑷ [mathjax]\((-4)²+25 \div (-5²)\)
⑸ [mathjax]\(\dfrac{1}{3}+\require{physics} \left(-\dfrac{2}{3}\right)^{2}\)
⑹ [mathjax]\(\dfrac{1}{4}-\dfrac{3}{7} \div \dfrac{4}{7}\)
分配法則
Q Question
次の㋐，㋑の計算をして，その結果を比べてみましょう。どんなことがわかるでしょうか。
⑴ ㋐ [mathjax]\((-5) \times \{(-4)+6\} \)
㋑ [mathjax]\((-5)\times (-4)+(-5) \times 6\)
⑵ ㋐ [mathjax]\(\{(-4)+6\} \times (-5)\)
㋑ [mathjax]\((-4) \times (-5)+6 \times (-5)\)
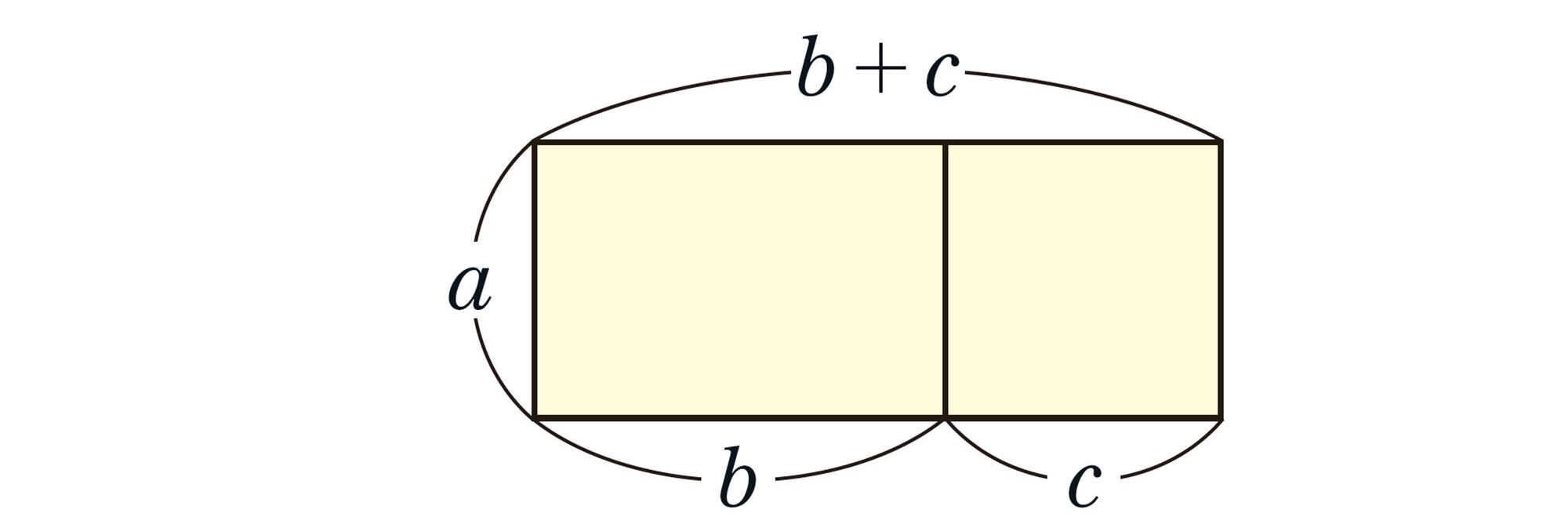
小学校では，[mathjax]\((a+b) \times c= a \times c + b \times c\)が成り立ったね。
負の数があっても，計算のきまりは成り立つのかな。
見方・考え方
負の数をふくむ計算も，計算のきまりが成り立つかな。
正の数，負の数でも，次のことが成り立つ。
分配法則
分配法則
[mathjax]\(a \times (b+c) = a \times b+a \times c \)は，左の式を右の式にしたり，右の式を左の式にしたりできるね。
例 ４
⑴
⑵
<1年p.49>
問 ５ 分配法則を利用して，次の計算をしなさい。
⑴ [mathjax]\(28 \times \require{physics} \left(-\dfrac{1}{4} + \dfrac{1}{7}\right)\)
⑵ [mathjax]\(\require{physics} \left(\dfrac{3}{4} – \dfrac{5}{6}\right) \times 36 \)
⑶ [mathjax]\(17 \times 9 + 17 \times (-8)\)
⑷ [mathjax]\(69 \times (-7.2) + 31 \times (-7.2)\)
やってみよう
計算力を高めよう2-4
P.53
どんなことがわかったかな
四則の混じった計算は，符号に注意すれば小学校の計算と同じようにできます。
次の課題へ！
正の数，負の数を学んで，どんなことができるようになったかな？
P.50,54
記号の由来「[mathjax] \(+\)，[mathjax] \(-\)」 Tea Break
現在，計算のために使われている記号は，15世紀から17世紀にかけて完成されたものがほとんどです。15世紀から17世紀はヨーロッパの「大航海時代」で，ヨーロッパの国々が，通商や植民地を求めて大西洋へ航海をしました。安全な航海のための天文観測や通商のための計算をすばやく行うことが必要となり，その専門家である「計算手」も現れました。計算手たちは，それまで長々と書いていた計算の式を，記号を使って簡便な形にしました。
右に示すのは，その一例です。
[mathjax] \(+\)，[mathjax] \(-\)の記号は，最初は過不足を表す符号として使われていましたが，その後，計算の記号としても使われるようになりました。これらの記号は，右のように文字を変形してできたという説があります。
＊et はラテン語で，英語の「and」と同じ意味
＊minusは「不足」の意味
＊本の中で記号が最初に使われた年と本の作者
<1年p.50>
４ 正の数・負の数の利用
負の数を使うと，どんなことができるかな。
身のまわりで，負の数を使う場面を考えてみよう。
Q Question
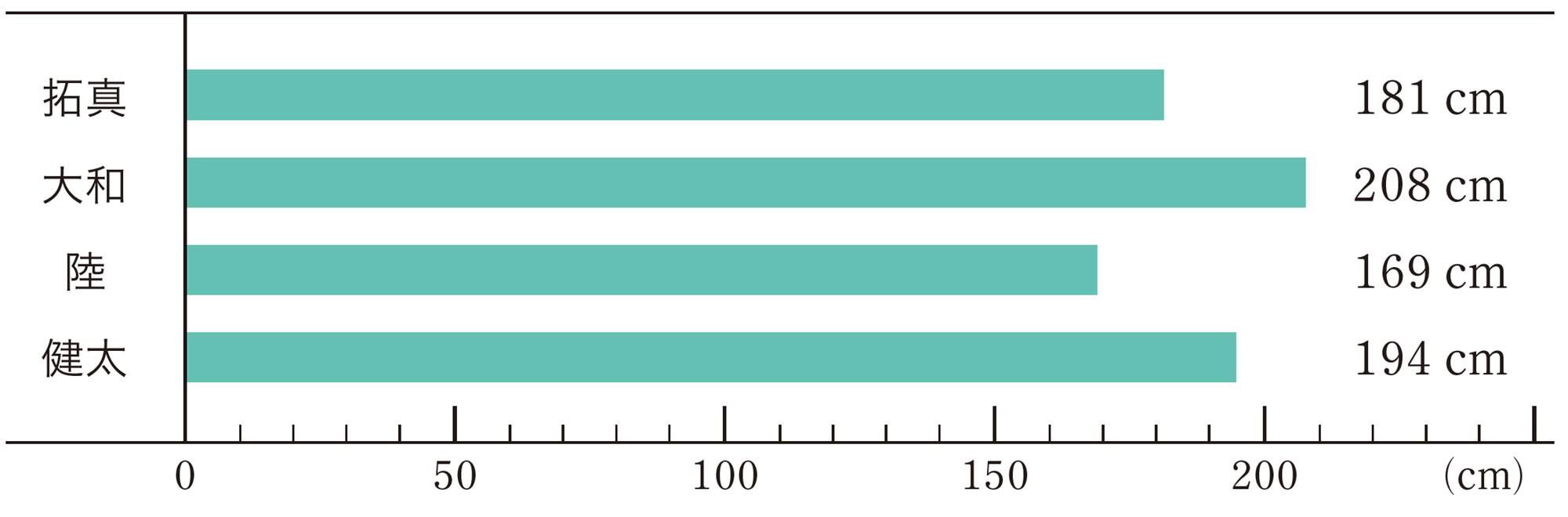
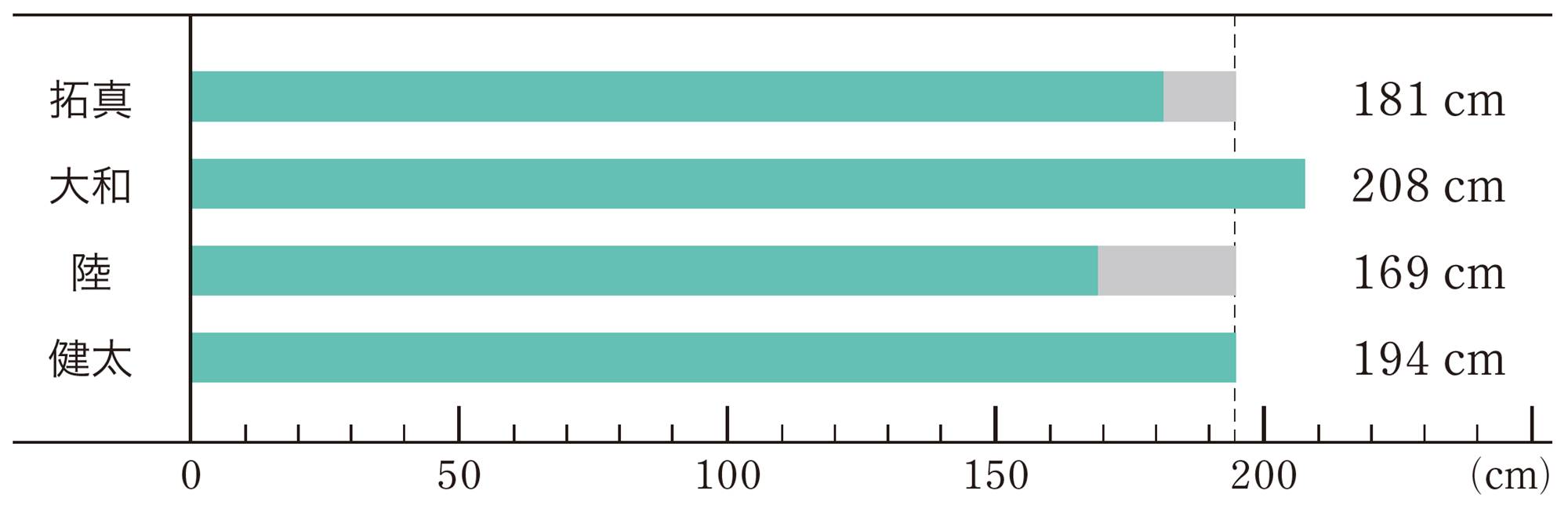
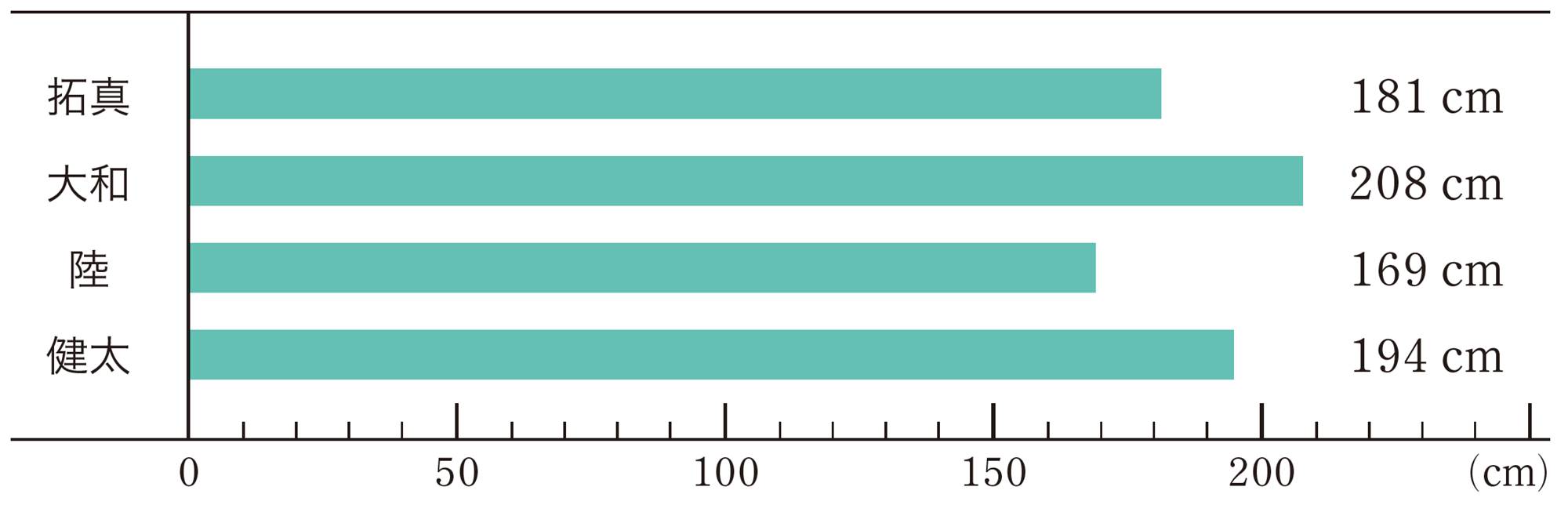
拓真さんの中学校で，新体力テストを行いました。次の表は，拓真さんと同じ班の男子4人の立ち幅とびの記録です。この表をもとに，4人の記録の平均を求めてみましょう。
記録の合計を4でわれば，平均が求められるね。
それぞれの記録の差が使えないかな。
見方・考え方
4人の記録の差に着目して考えられるかな。
目標 ▷ 正の数，負の数を利用して，身のまわりの問題を解決しよう。
１ 美月さんは，次の式にあてはめて平均を求めました。
[mathjax]\(\text{（平均）}=\text{（データの値の合計）}\div \text{（データの個数）}\)
美月さんの考え方で平均を求めましょう。
式にあてはめればできるけど，もっと効率的な方法はないかな。
数値が大きくなっても，簡単にできる方法はないかな。
２ この章で学習したことを使って，効率的に平均を求める方法を考えましょう。
<1年p.51>
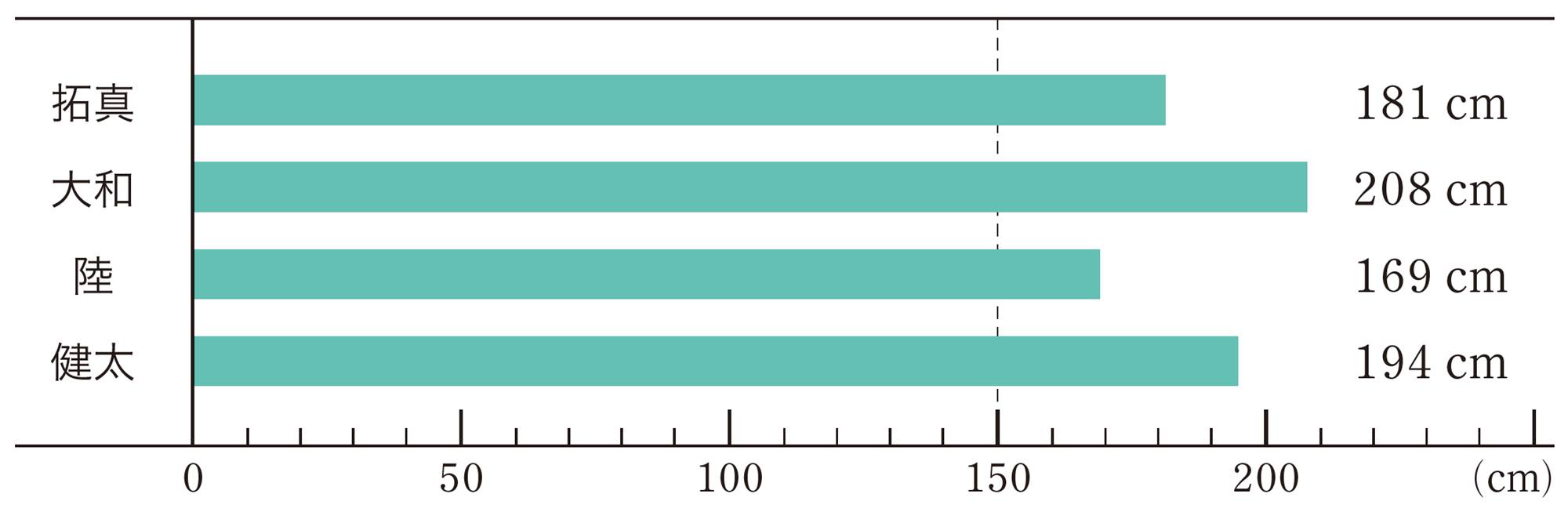
３ 拓真さんは，4人の記録がすべて150cm 以上であることに着目し，150cmを基準として平均を求めようと考え，式をつくりました。
式 [mathjax]\(150+(31+58+19+44) \div 4\)
拓真さんの式の意味を説明しましょう。また，この考え方で平均を求め，【1】 で求めた値と比べましょう。
４ 健太さんは，自分の記録194cm を基準として，平均を求める式をつくりました。健太さんの考え方で式をつくり，平均を求めましょう。
５ 基準を何cmとすると，平均を求めやすいでしょうか。自分で基準を決めて，平均を求めましょう。
６ 平均を求めるとき，どんなくふうができるかをまとめましょう。
<1年p.52>
問 １ 右の値は，真央さんのクラスの女子12人の50m 走の記録です。基準を決めて，12人の記録の平均を求めなさい。
（単位：秒）
どんなことがわかったかな
正の数，負の数を利用すると，平均を効率的に求めることができる場合があります。
確かめよう 3節 乗法・除法
□ 正の数，負の数の乗法の計算をすることができる。 乗法 P.38例1例2 P.41例4 P.42例6
１ 次の計算をしなさい。
⑴ [mathjax]\((+8) \times (-9)\)
⑵ [mathjax]\((-7)\times (-3)\)
⑶ [mathjax]\(-10 \times 6\)
⑷ [mathjax]\(8 \times (-2)\times (-4)\)
⑸ [mathjax] \((-7)²\)
⑹ [mathjax] \(-6²\)
□ 正の数，負の数の除法の計算をすることができる。 除法 P.44例2例3 P.45例4
２ 次の計算をしなさい。
⑴ [mathjax]\((-27) \div (+3)\)
⑵ [mathjax]\((-30) \div (-6)\)
⑶ [mathjax]\(15 \div (-9)\)
⑷ [mathjax]\(\require{physics} \left(-\dfrac{5}{8}\right) \div \require{physics} \left(-\dfrac{3}{4}\right)\)
□ 正の数，負の数の乗法と除法の混じった計算をすることができる。 乗法と除法の混じった計算 P.46例5
３ 次の計算をしなさい。
⑴ [mathjax]\(24 \div (-6) \times (-2)\)
⑵ [mathjax]\(5 \times (-4) \div \dfrac{2}{3}\)
□ 正の数，負の数の四則の混じった計算をすることができる。 四則の混じった計算 P.47例1例2例3
４ 次の計算をしなさい。
⑴ [mathjax]\(10+2 \times (-7)\)
⑵ [mathjax]\((-4) -15 \div (-3)\)
⑶ [mathjax]\(-5 \times (6-9)\)
⑷ [mathjax]\(18+4 \times (1-7)\)
⑸ [mathjax]\(16 \div (-4)²\)
⑹ [mathjax]\(12-5²\)
□ 分配法則を使って，正の数，負の数の計算をすることができる。 分配法則 P.48例4
５ 分配法則を利用して，次の計算をしなさい。
⑴ [mathjax]\(\require{physics} \left(-\dfrac{1}{6}+ \dfrac{7}{9}\right) \times 18\)
⑵ [mathjax]\((-6) \times 55 + (-6) \times 45\)
<1年p.53>
計算力を高めよう 2
家庭学習や計算練習で利用しましょう。
乗法・除法 解答P.302
１ 乗法
⑴ [mathjax]\((+2) \times (+5)\)
⑵ [mathjax]\((+3) \times (-8)\)
⑶ [mathjax]\((-4) \times (+9)\)
⑷ [mathjax]\((-6) \times (-7)\)
⑸ [mathjax]\(2 \times (-6) \times (+10)\)
⑹ [mathjax]\(-3 \times 8 \times (-2)\)
⑺ [mathjax] \((-9)²\)
⑻ [mathjax] \(-9²\)
⑼ [mathjax] \((-4)³\)
⑽ [mathjax] \(0.7²\)
⑾ [mathjax]\(\require{physics} \left(-\dfrac{3}{5}\right)\times \require{physics} \left(+\dfrac{5}{8}\right)\)
⑿ [mathjax]\(8 \times \require{physics} \left(-\dfrac{1}{4}\right) \times (-7)\)
２ 除法
⑴ [mathjax]\((+12) \div (+6)\)
⑵ [mathjax]\((+10) \div (-2)\)
⑶ [mathjax]\((-18) \div (+6)\)
⑷ [mathjax]\((-42) \div (-4)\)
⑸ [mathjax]\(0 \div (-3)\)
⑹ [mathjax]\((+3.2) \div (-8)\)
⑺ [mathjax]\(\require{physics} \left(-\dfrac{2}{3}\right) \div 6\)
⑻ [mathjax]\((-12) \div \require{physics} \left(-\dfrac{4}{7}\right)\)
⑼ [mathjax]\(\dfrac{5}{8} \div \require{physics} \left(-\dfrac{3}{4}\right)\)
３ 乗法と除法の混じった計算
⑴ [mathjax]\((-4) \div (-2) \times 7\)
⑵ [mathjax]\(20 \times (-3) \div (-5)\)
⑶ [mathjax]\(6 \div (-9) \times 15\)
⑷ [mathjax]\((-3) \times 6 \div (-12)\)
⑸ [mathjax]\((-48) \div (-8) \div (-4)\)
⑹ [mathjax]\(\dfrac{2}{3} \div \require{physics} \left(-\dfrac{9}{4}\right) \times 4\)
⑺ [mathjax]\(\dfrac{1}{7} \times \require{physics} \left(-\dfrac{10}{9}\right) \div \require{physics} \left(-\dfrac{5}{14}\right)\)
４ 四則の混じった計算
⑴ [mathjax]\((-4)+2 \times (-3)\)
⑵ [mathjax]\(-8-6 \times 3\)
⑶ [mathjax]\(18-72 \div (-9)\)
⑷ [mathjax]\(3 \times (-7-5)\)
⑸ [mathjax]\((5-19) \div (-2)\)
⑹ [mathjax]\(4 \times (-2)+(-14) \div 2\)
⑺ [mathjax]\(36 \div (-2)²\)
⑻ [mathjax]\(10-4²\)
⑼ [mathjax]\((-5)²+(-5²)\)
⑽ [mathjax]\((-45) \div 3²+15\)
⑾ [mathjax]\(20+6 \times (7-10)\)
⑿ [mathjax]\(12-7 \times \{8+(-9)\}\)
⒀ [mathjax]\(\dfrac{3}{4} + \require{physics} \left(-\dfrac{2}{3}\right) \div 2\)
⒁ [mathjax]\(\dfrac{7}{9}-\require{physics} \left(-\dfrac{1}{3}\right)^{2}\)
