<1年p.43>
２ 除法
Q Question
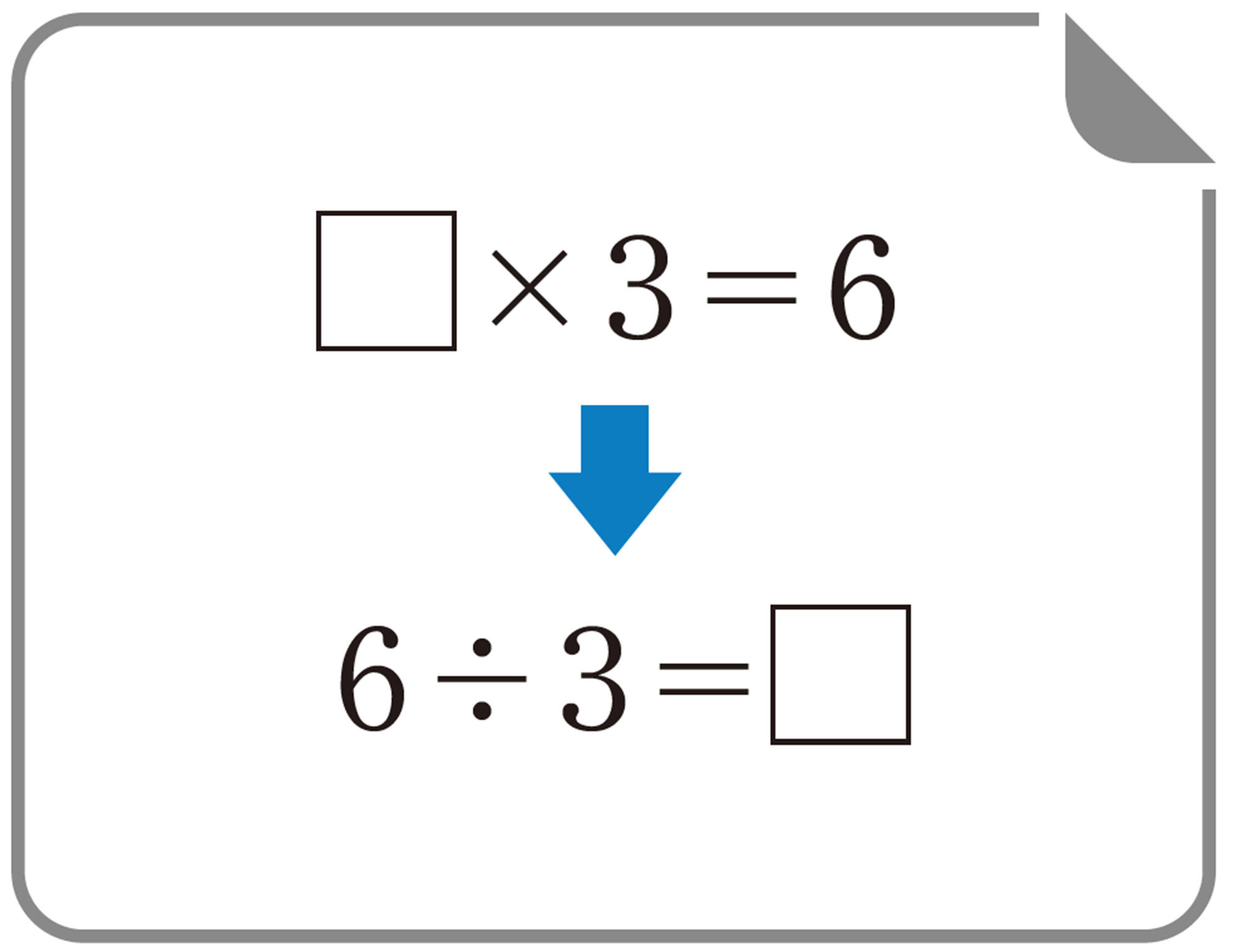
[mathjax]\(\boxed{\phantom{00}}\times 3=6\) の[mathjax]\(\boxed{\phantom{00}}\)を求めるにはどうしたらよいでしょうか。これをもとに，次の[mathjax]\(\boxed{\phantom{000}}\)にあてはまる数を求めてみましょう。
⑴ [mathjax]\((\boxed{\phantom{000}})\times (+2)=+6\)
⑵ [mathjax]\((\boxed{\phantom{000}})\times (+2)=-6\)
⑶ [mathjax]\((\boxed{\phantom{000}})\times (-2)=+6\)
⑷ [mathjax]\((\boxed{\phantom{000}})\times (-2)=-6\)
かけられる数を求めるときは，わり算で考えたね。
負の数があっても，わり算で考えていいのかな。
見方・考え方
小学校で学んだわり算と同じように考えられるかな。
上の式の[mathjax]\(\boxed{\phantom{000}}\)にあてはまる数を求める計算は，乗法の逆の計算であり，それがわり算である。
わり算のことを 除法 という。その結果が商である。
目標 ▷ 正の数，負の数の除法を考えよう。
例 １ 【Q】⑴ ，⑵について，除法の式を考えると，次のようになる。
⑴ [mathjax]\((+3)\times (+2)=+6\) であるから，[mathjax]\((+6)\div (+2)=+3\)
⑵ [mathjax]\((-3)\times (+2)=-6\) であるから，[mathjax]\((-6)\div(+2)=-3\)
問 １ 【Q】⑶ ，⑷について，次の[mathjax]\(\square \)にあてはまる数を書き入れなさい。
⑶ [mathjax]\((\boxed{\phantom{000}})\times (-2)=+6\) であるから，[mathjax]\((+6)\div (-2)=\boxed{\phantom{000}}\)
⑷ [mathjax]\((\boxed{\phantom{000}})\times (-2)=-6\) であるから，[mathjax]\((-6) \div (-2)=\boxed{\phantom{000}}\)
問 ２ 正の数，負の数の除法では，商の符号や絶対値は，わられる数，わる数の2数の符号や絶対値とどんな関係がありますか。例1，問1の4つの除法の式をもとに説明しなさい。
積と同じように考えられるかな。
<1年p.44>
符号や絶対値に着目した除法
例 ２ 同符号の2数の商
⑴
[mathjax]\((+) \div (+) \rightarrow (+)\)
⑵
[mathjax]\((-) \div (-) \rightarrow (+)\)
例 ３ 異符号の2数の商
⑴
[mathjax]\((+) \div (-) \rightarrow (-)\)
⑵
[mathjax]\((-) \div (+) \rightarrow (-)\)
正の数，負の数の除法について，次のようにまとめることができる。
正の数，負の数の除法
[mathjax]\(0\div (+2)=0\)，[mathjax]\(0 \div(-6)=0\)のように，0を正の数，負の数でわったとき，商は0になる。
0でわることはできるのかな？
問 ３ 次の計算をしなさい。
⑴ [mathjax]\((+10) \div (+2)\)
⑵ [mathjax]\((-8) \div (-4)\)
⑶ [mathjax]\((+16) \div (-2)\)
⑷ [mathjax]\((-24) \div (+8)\)
⑸ [mathjax]\(0 \div (-5)\)
⑹ [mathjax]\((-3) \div (-6)\)
⑺ [mathjax]\((+84) \div (-12)\)
⑻ [mathjax]\((-1.2) \div (+4)\)
⑼ [mathjax]\((-6.3) \div (-9)\)
<1年p.45>
除法と逆数
Q Question
次の分数の除法は，どのように計算すればよいか考えてみましょう。
[mathjax]\(\require{physics} \left(+\dfrac{5}{7}\right) \div \require{physics} \left(- \dfrac{2}{3}\right)\)
分数の除法は，わる数を逆数にして，乗法に変えたね。
負の数にも逆数はあるのかな。
見方・考え方
小学校で学んだ分数のわり算と同じように考えられるかな。
除法は，わる数を逆数にすると，乗法として考えることができた。
負の数でも逆数を考えることができる。
たとえば，
[mathjax]\(\require{physics} \left(- \dfrac{2}{3}\right)\times\require{physics} \left(-\dfrac{3}{2}\right)=1\)
であるから，[mathjax]\(- \dfrac{2}{3}\)の逆数は[mathjax]\(- \dfrac{3}{2}\) ，[mathjax]\(- \dfrac{3}{2}\)の逆数は[mathjax]\(- \dfrac{2}{3}\)である。
注意 0とどんな数との積も0であり，1にならないから，0の逆数はない。
ふりかえり 小学校6年
2つの数の積が1になるとき，一方の数を，もう一方の数の逆数という。
問 ４ 次の数の逆数を求めなさい。
⑴ [mathjax]\(- \dfrac{4}{7}\)
⑵ [mathjax]\(- \dfrac{1}{6}\)
⑶ [mathjax] \(-5\)
⑷ [mathjax] \(-1\)
問 ５ 次の㋐，㋑の計算をして，その結果を比べなさい。
㋐ [mathjax]\(15 \div (-3)\)
㋑ [mathjax]\(15 \times \require{physics} \left(-\dfrac{1}{3}\right)\)
上のことから，正の数，負の数の除法について，次のことがわかる。
正の数，負の数でわることは，その数の逆数をかけることと同じである。
例 ４
⑴
⑵
<1年p.46>
問 ６ 次の計算をしなさい。
⑴ [mathjax]\(\require{physics} \left(-\dfrac{1}{3}\right) \div \dfrac{3}{4}\)
⑵ [mathjax]\(\require{physics} \left(-\dfrac{3}{5}\right) \div \require{physics} \left(-\dfrac{9}{10}\right)\)
⑶ [mathjax]\(6 \div \require{physics} \left(-\dfrac{4}{3}\right)\)
⑷ [mathjax]\(\require{physics} \left(-\dfrac{5}{6}\right) \div (-3)\)
P.53
乗法と除法の混じった計算
例 ５
除法を乗法に直す
乗法に直せば，交換法則・結合法則が使えるね。
乗法と除法の混じった計算は，乗法だけの式に直して計算するとよい。
問 ７ 次の計算をしなさい。
⑴ [mathjax]\((-8) \div 2 \times (-4)\)
⑵ [mathjax]\(20 \times (-5) \div \require{physics} \left(-\dfrac{1}{3}\right)\)
⑶ [mathjax]\(6\div \require{physics} \left(-\dfrac{2}{3}\right)\times \require{physics} \left(-\dfrac{5}{9}\right)\)
⑷ [mathjax]\(\dfrac{2}{3} \div \require{physics} \left(-\dfrac{3}{8}\right)\div 4\)
P.53
これまでに学んだ加法，減法，乗法，除法をまとめて 四則 という。
どんなことがわかったかな
正の数，負の数の除法は，わる数を逆数にして，乗法に直して計算できます。
次の課題へ！
四則の混じった計算は，小学校の計算と同じように計算の順序があるのかな？
P.47
0でわることはできる？ Tea Break
数学では，「[mathjax]\(3 \div 0\)」，「[mathjax]\(0 \div 0\)」などの0でわる除法は考えません。その理由を，次のように考えてみましょう。
① [mathjax]\(3 \div 0=\boxed{\phantom{00}}\)とすると，[mathjax]\(\boxed{\phantom{00}}\times 0 = 3\)となります。この[mathjax]\(\boxed{\phantom{00}}\)にあてはまる数はないので，[mathjax]\(3 \div 0\)の商はありません。
② [mathjax]\(0 \div 0=\boxed{\phantom{00}}\)とすると，[mathjax]\(\boxed{\phantom{00}}\times 0=0\)となります。この[mathjax]\(\boxed{\phantom{00}}\)にはどんな数をあてはめても成り立つので，[mathjax]\(0 \div 0 \)の商は1つに決まりません。
