<1年p.30>
３ 加法と減法の混じった計算
Q Question
次の加法と減法の混じった式を計算するには，どんなくふうをすればよいでしょうか。
⑴ [mathjax]\((+2)+(-5)-(-4)\)
⑵ [mathjax]\((-6)-(+7)-(-6)\)
見方・考え方
符号に着目して考えられるかな。
加法と減法が混じっているとわかりにくいね。
減法と同じように，加法に直せばいいのかな。
目標 ▷ 加法と減法の混じった計算を考えよう。
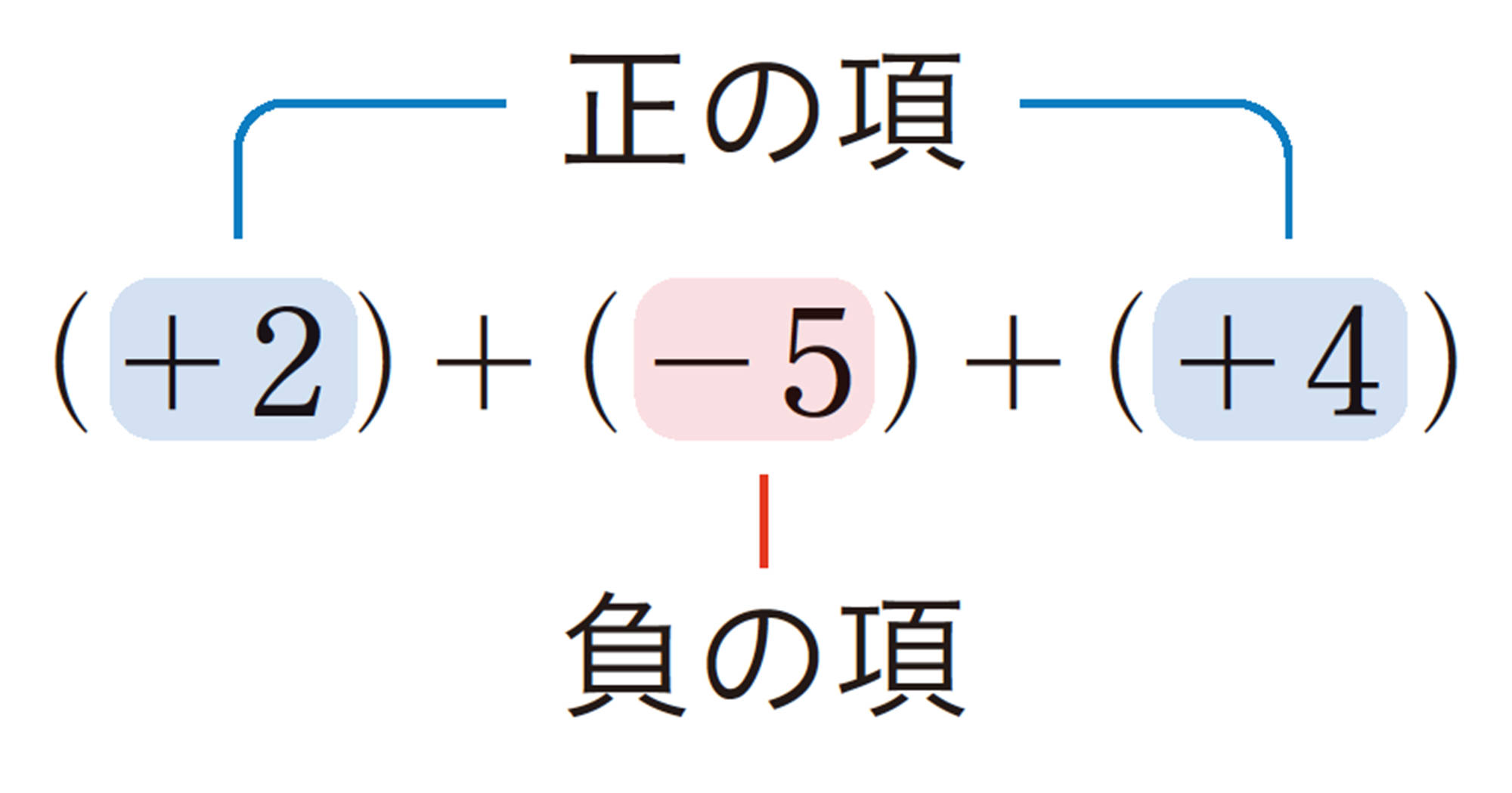
加法と減法の混じった式は，右のように，加法だけの式に直すことができる。
加法の式[mathjax]\((+2)+(-5)+(+4)\)で，加法の記号[mathjax]\(+\)で結ばれた[mathjax] \(+2\)，[mathjax] \(-5\)，[mathjax] \(+4\)を，この式の 項 という。また，[mathjax] \(+2\)，[mathjax] \(+4\)を 正の項 ，[mathjax] \(-5\)を負の項 という。
問 １ 次の式を加法だけの式に直しなさい。また，正の項，負の項をそれぞれいいなさい。
⑴ [mathjax]\((+4)-(-3)\)
⑵ [mathjax]\((+7)-(+2)\)
⑶ [mathjax]\((-9)+(-4)-(-6)\)
⑷ [mathjax]\((-5)-(-3)-(-8)\)
加法の式では，右のように，加法の記号[mathjax]\(+\)やかっこを省いて，項だけを並べて表すことができる。また，式の最初の項が正の数のときは，正の符号[mathjax]\(+\)を省くことができる。
<1年p.31>
問 ２ 次の式を加法の式に直してから，かっこを省いて，項だけを並べた式に直しなさい。
⑴ [mathjax]\((+10)-(+15)\)
⑵ [mathjax]\((-7)-(-9)\)
⑶ [mathjax]\((-1)+(-4)-(-7)\)
⑷ [mathjax]\((+6)-(-8)-(+16)\)
⑸ [mathjax]\((+7)-(+3)+(-5)-(-1)\)
⑹ [mathjax]\((-2)+(+9)-(+1)-(-4)\)
問 ３ 次の式を加法の記号[mathjax]\(+\)とかっこを使って表しなさい。
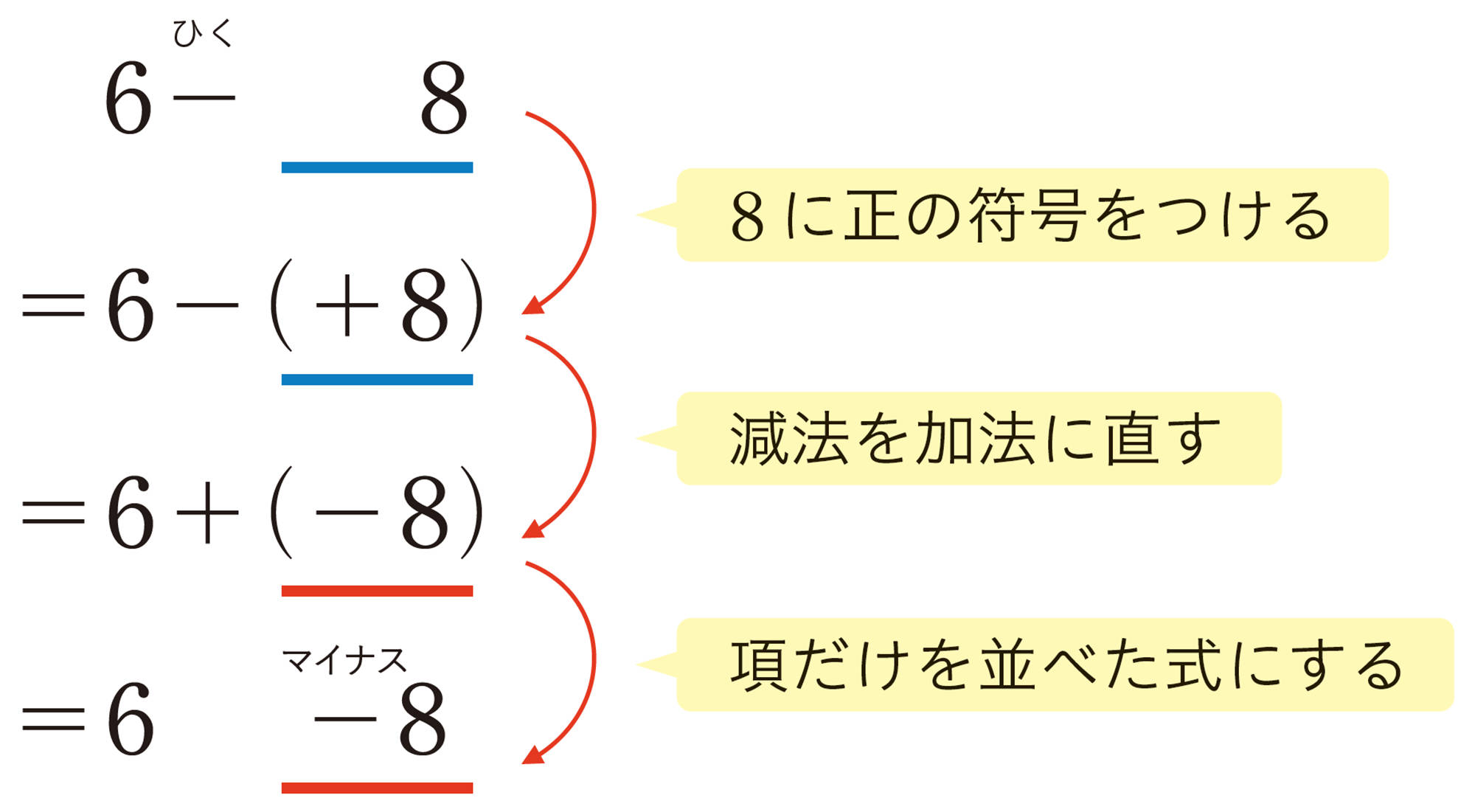
⑴ [mathjax]\(6-8\)
⑵ [mathjax]\(-14-13\)
⑶ [mathjax]\(-4+9-7\)
⑷ [mathjax]\(7-8+6-2\)
項を並べた式は，交換法則や結合法則を使って，次のように計算することができる。また，答えの正の符号[mathjax]\(+\)も省くことができる。
問 ４ 問2の項を並べた式と，問3の式を，それぞれ計算しなさい。
例 １ [mathjax]\(7+(-8)-5-(-4)\)を計算しなさい。
考え方 かっこのついた加法や減法の形で書かれた部分を，項を並べた形に直して計算する。
解答
答 [mathjax]\(-2\)
式の説明なども書いておこう。
<1年p.32>
問 ５ 次の計算をしなさい。
⑴ [mathjax]\(-3+(-2)-(-9)\)
⑵ [mathjax]\(8-(+7)-5\)
⑶ [mathjax]\(-2-(-3)+7+(-4)\)
⑷ [mathjax]\(3+(-8)-(-5)-1\)
問 ６ 次の計算をしなさい。
⑴ [mathjax]\(11-17+13\)
⑵ [mathjax]\(-14+19+12-19\)
⑶ [mathjax]\(-3.1-5.9\)
⑷ [mathjax]\(-0.6-(-1)\)
⑸ [mathjax] \(\dfrac{1}{6}-\dfrac{3}{4}\)
⑹ [mathjax] \(-\dfrac{2}{7} +\dfrac{6}{7}- \dfrac{3}{7}\)
どんなことがわかったかな
加法と減法の混じった計算も，減法を加法に直して，項を並べた形の式に直せば計算できます。
次の課題へ！
「[mathjax]\(6-8\)」の計算と意味 Tea Break
「6ひく8」のような，ひかれる数よりひく数の方が大きい減法は，小学校では考えませんでした。しかし，正の数と0のほかに，負の数を用いることで，これらの減法もできるようになりました。
「[mathjax]\(6-8\)」の式は，「6ひく8」とみることもできますが，30ページで学んだように，項だけを並べた加法の式，つまり「6たす[mathjax] \(-8\)」とみることができます。これらが同じであることは，次のように説明することができます。
[mathjax]\(\begin{eqnarray}& & 6- 8\\
&=& 6- (+8)\\
&=& 6+ (-8)\\
&=& 6 -8\end{eqnarray}\)
「[mathjax]\(6-8\)」の「[mathjax]\(-\)」は減法の記号と考えても，負の符号と考えてもいいんだね。
<1年p.33>
確かめよう ２節 加法・減法
１ 次の計算をしなさい。
⑴ [mathjax]\((+3)+(-2)\)
⑵ [mathjax]\((-4)+(-6)\)
⑶ [mathjax]\((-14)+(+5)\)
⑷ [mathjax]\((-8)+(+8)\)
□ 正の数，負の数の減法の計算をすることができる。減法 P.27例2P.28問5
２ 次の計算をしなさい。
⑴ [mathjax]\((+2)-(+9)\)
⑵ [mathjax]\((+1)-(-5)\)
⑶ [mathjax]\((-6)-(-17)\)
⑷ [mathjax]\(0-(-12)\)
□ 正の数，負の数の加法と減法の混じった計算をすることができる。 加法と減法の混じった計算 P.31問4例1
３ 次の計算をしなさい。
⑴ [mathjax]\((+5)+(-18)+(-5)\)
⑵ [mathjax]\((-9)-(-8)+(-4)\)
⑶ [mathjax]\(2-7\)
⑷ [mathjax]\(-4-5\)
⑸ [mathjax]\(-2+10-5\)
⑹ [mathjax]\(3-7-4+8\)
⑺ [mathjax]\(16-(+17)-13\)
⑻ [mathjax]\((-3)+6+(-7)-(-9)\)
減法でも交換法則・結合法則は成り立つの？ Tea Break
24ページで，正の数，負の数の加法でも，
交換法則 [mathjax]\(a+b=b+a\)
結合法則 [mathjax]\((a+b)+c=a+(b+c)\)
が成り立つことを学びました。減法でも，同じように交換法則・結合法則が成り立つでしょうか。
次の⑴，⑵で，㋐，㋑をそれぞれ比べてみましょう。
⑴ ㋐ [mathjax]\((+2)-(-3)\)
㋑ [mathjax]\((-3)-(+2)\)
⑵ ㋐ [mathjax]\(\{(+2)-(-3)\}-(+5)\)
㋑ [mathjax]\((+2)-\{(-3)-(+5)\}\)
⑴，⑵は，それぞれ㋐と㋑の答えが異なります。
⑴の㋐，㋑からは交換法則が，⑵の㋐，㋑からは結合法則が成り立っていないことがわかります。
したがって，減法では，交換法則も結合法則も成り立たないといえます。
ただし，減法を加法に直すことで，交換法則・結合法則が使えるようになります。
<1年p.34>
計算力を高めよう 1
家庭学習や計算練習で利用しましょう。
加法・減法 解答P.302
１ 加法
⑴ [mathjax]\((+11)+(+4)\)
⑵ [mathjax]\((-6)+(-12)\)
⑶ [mathjax]\((+8)+(-1)\)
⑷ [mathjax]\((+3)+(-10)\)
⑸ [mathjax]\((+16)+(-16)\)
⑹ [mathjax]\((-7)+(+2)\)
⑺ [mathjax]\((-9)+(+13)\)
⑻ [mathjax]\((+0.6)+(-1.8)\)
⑼ [mathjax]\((-2.7)+(-3.5)\)
⑽ [mathjax]\(\require{physics}\left(-\dfrac{1}{3}\right)+\require{physics}\left(+\dfrac{1}{2}\right)\)
⑾ [mathjax]\(\require{physics}\left(-\dfrac{3}{4}\right)+\require{physics}\left(-\dfrac{5}{12}\right)\)
２ 減法
⑴ [mathjax]\((+8)-(+4)\)
⑵ [mathjax]\((+3)-(+9)\)
⑶ [mathjax]\((+5)-(-2)\)
⑷ [mathjax]\(0-(-13)\)
⑸ [mathjax]\((-7)-(+2)\)
⑹ [mathjax]\((-9)-(-1)\)
⑺ [mathjax]\((-2)-(-15)\)
⑻ [mathjax]\((-1.9)-(+1.4)\)
⑼ [mathjax]\(\require{physics}\left(+\dfrac{1}{6}\right)-\require{physics}\left(-\dfrac{1}{2}\right)\)
⑽ [mathjax]\(\require{physics}\left(-\dfrac{2}{7}\right)-\require{physics}\left(+\dfrac{5}{14}\right)\)
⑾ [mathjax]\(\require{physics}\left(-\dfrac{5}{3}\right)-(-3)\)
３ 加法と減法の混じった計算
⑴ [mathjax]\((-3)+(+2)-(+5)\)
⑵ [mathjax]\((+6)-(-7)+(-13)\)
⑶ [mathjax]\((-6)-(+1)+(-3)-(-8)\)
⑷ [mathjax]\(3-8\)
⑸ [mathjax]\(-6+9\)
⑹ [mathjax]\(-7-4\)
⑺ [mathjax]\(-18+18\)
⑻ [mathjax]\(5-19\)
⑼ [mathjax]\(-2+6-8\)
⑽ [mathjax]\(7-9-5\)
⑾ [mathjax]\(4-7+10-1\)
⑿ [mathjax]\(-12+4-3+7\)
⒀ [mathjax]\(0.4-1.9\)
⒁ [mathjax]\(-1.3+2.7\)
⒂ [mathjax]\(-\dfrac{2}{5} – \dfrac{3}{5}\)
⒃ [mathjax]\(\dfrac{4}{9} – \dfrac{5}{6}\)
⒄ [mathjax]\(-2 +(-10) -6\)
⒅ [mathjax]\(13 +(-2) -5 -(-7)\)
⒆ [mathjax]\(-7 -(+8) -(-3) +9\)
⒇ [mathjax]\(1 +(-0.6) -0.8\)
（21） [mathjax]\(-\dfrac{1}{3}+\dfrac{1}{6}-\require{physics}\left(-\dfrac{2}{3}\right)\)
