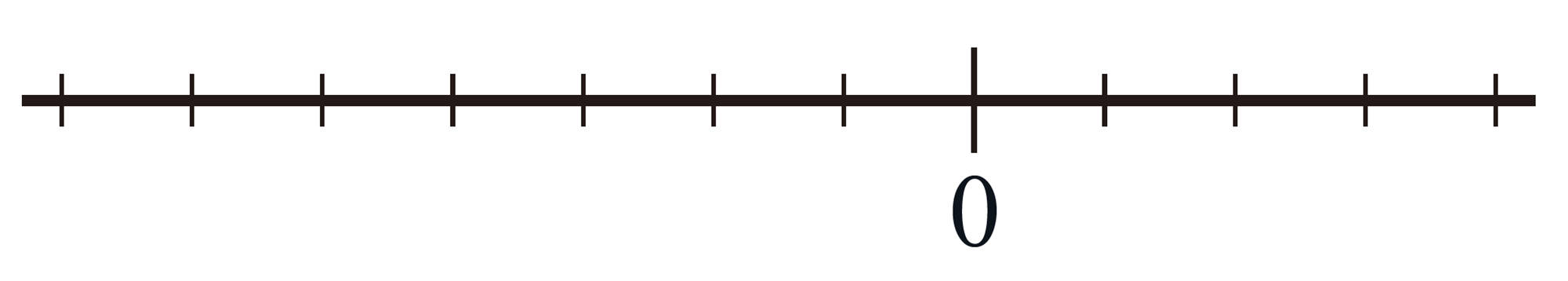<1年p.19>
２節 加法・減法
負の数があっても，計算できるかな？
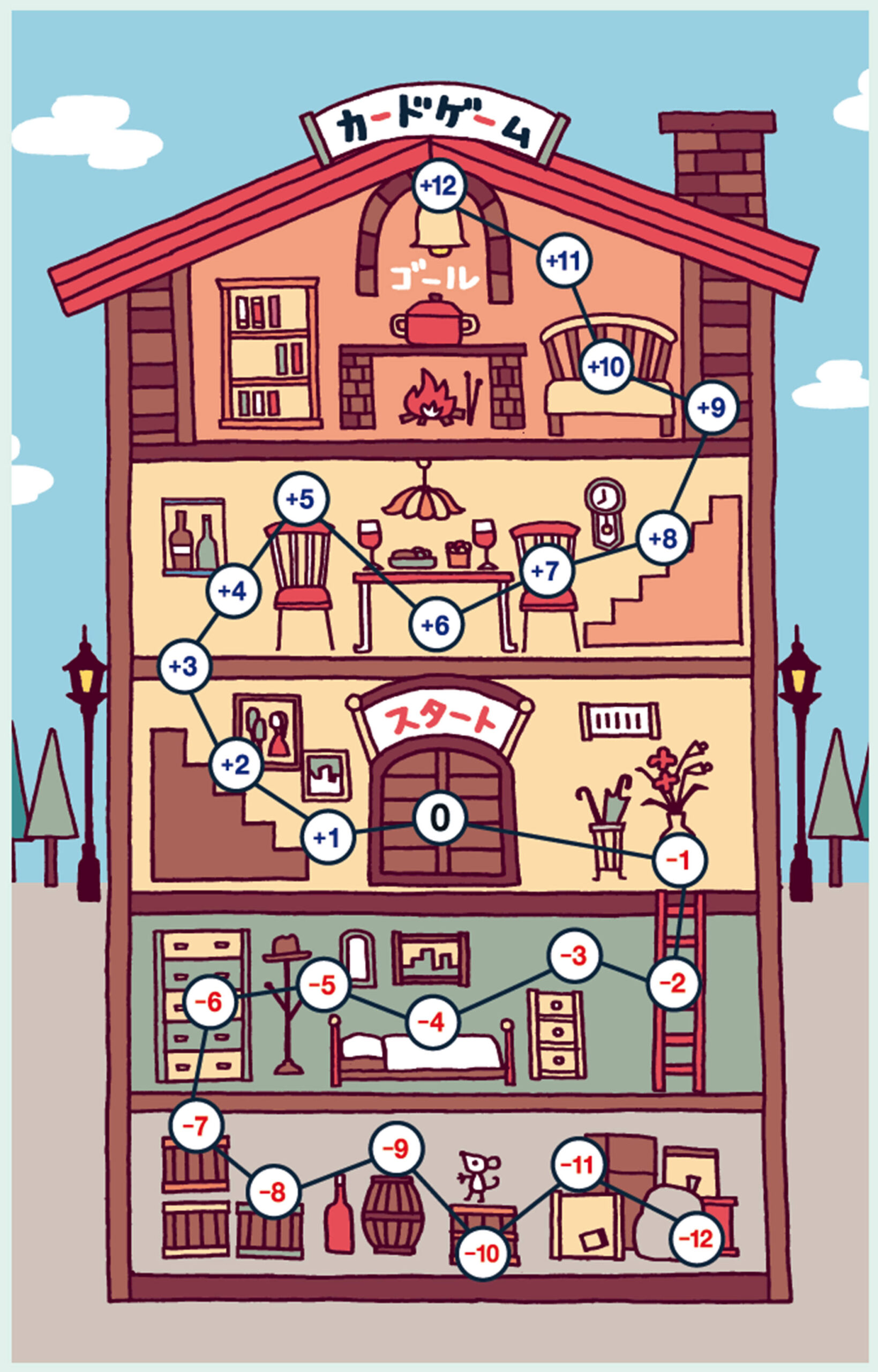
【１】 巻末①のカードゲームをしましょう。
ルール
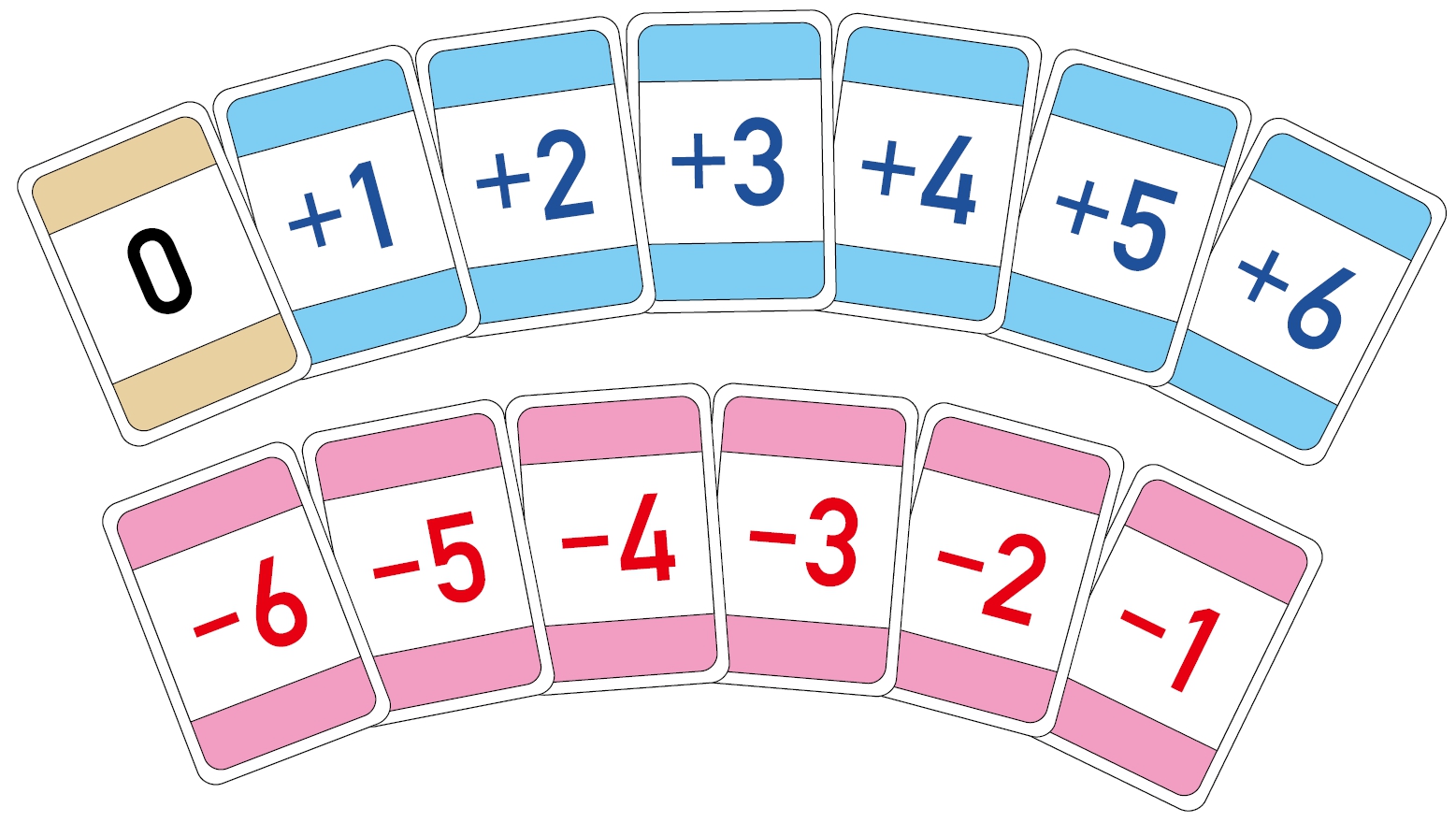
右下のような13枚のカードをよく混ぜ，裏返しにして重ねる。スタート0にコマを置き，順番にカードを取って，出た数だけ動かす。コマが先にゴールに着いた人が勝ちとなる。
コマの動かし方
[mathjax]\(\bbox[lightskyblue,3pt]{\phantom{0}+2\phantom{+}}\)が出たら，ゴールの方向へ2動かす。
[mathjax]\(\bbox[lightpink,3pt]{ \phantom{0}-3\phantom{+}}\)が出たら，ゴールと反対の方向へ3動かす。
[mathjax]\(\bbox[burlywood,3pt]{\phantom{+0} 0\phantom{+0}}\)が出たら，そのまま動かさない。
｢[mathjax]\(-\)｣のカードを取ると，ゴールから遠ざかるね。
｢[mathjax]\(+\)｣のカードを取らないと勝てないね。
次の課題へ！
正の数，負の数のたし算も小学校のときと同じようにできるのかな？
P.20
<1年p.20>
１ 加法
Q Question
前ページのカードゲームで，1 回目に[mathjax] \(+5\)，2 回目に[mathjax] \(+3\)のカードが出たとき，コマのある位置を計算で求めるにはどうしたらよいでしょうか。また，2 回目に[mathjax] \(-3\)のカードが出たときはどうしたらよいでしょうか。
2回の動きを合わせるから，たし算で表せそうだね。
負の数があっても，たし算で表していいのかな。
見方・考え方 具体的な場面を式に表せるかな。
目標 ▷ 正の数，負の数のたし算を考えよう。
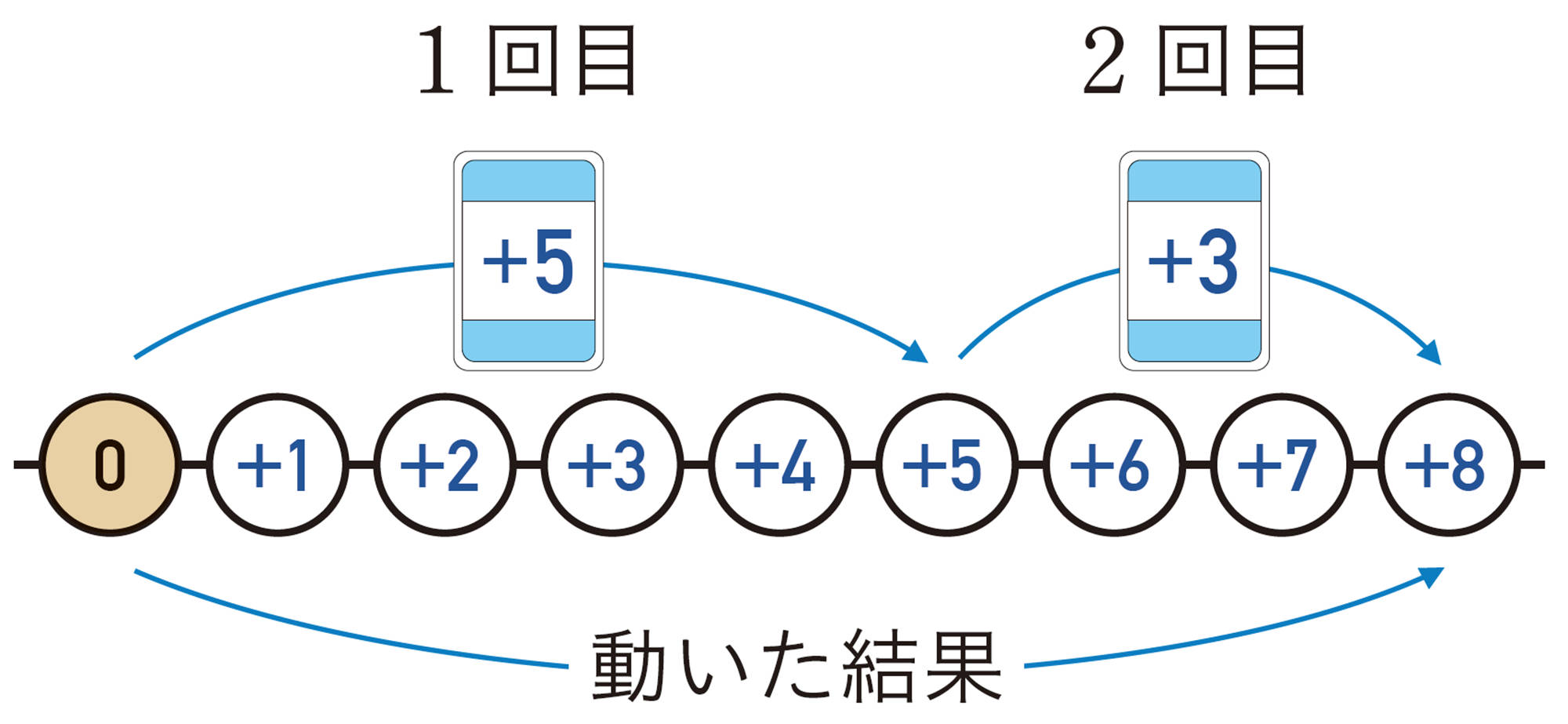
前ページのカードゲームで，1回目に[mathjax] \(+5\)，2回目に[mathjax] \(+3\)のカードが出たとすると，動いた結果は[mathjax] \(+8\)となる。
このことは，次のようなたし算の式で表すことができる。
[mathjax]\( (+5) + (+3) = +8\)
[mathjax]\((\mathsf{1回目の動き})+(\mathsf{ 2回目の動き})=(\mathsf{動いた結果})\)
問 １ 前ページのカードゲームで，次の表の㋐，㋑，㋒の場合について，動いた結果を求めるたし算の式を書き入れなさい。
<1年p.21>
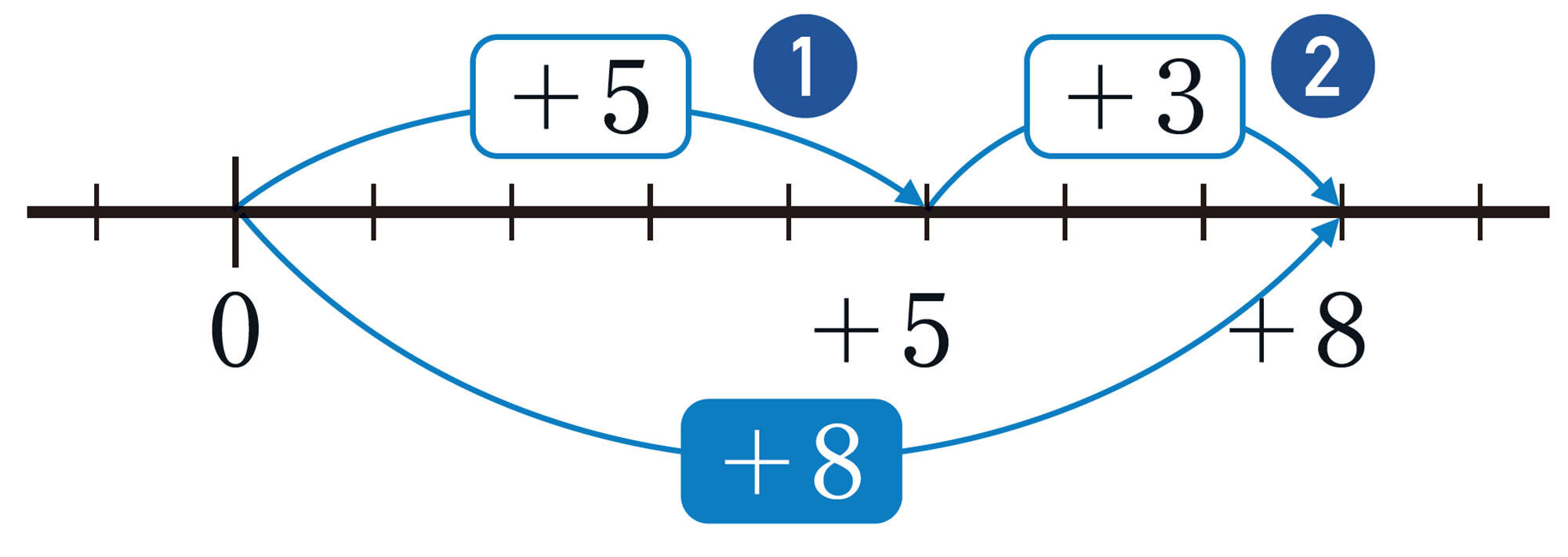
前ページでつくったたし算の式の計算を，数直線を使って考えてみよう。
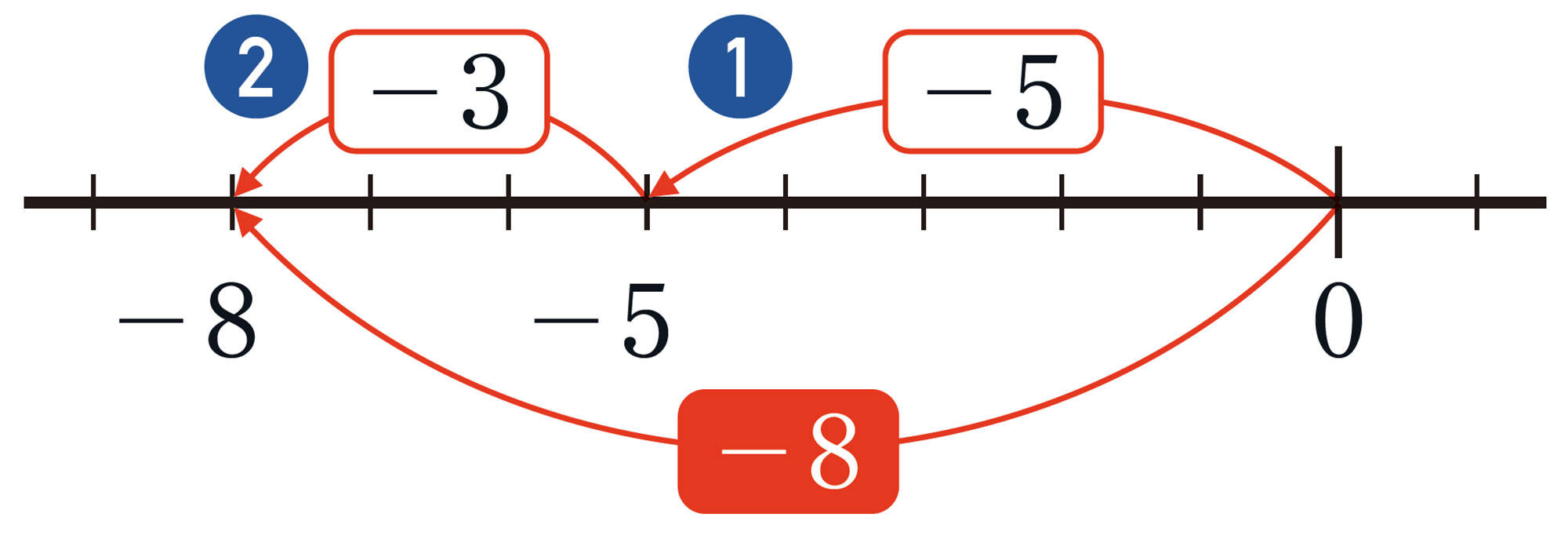
例１ 同符号の2数のたし算
⑴ [mathjax]\((+5)+(+3)\)
❶ 0から正の方向へ5動く。
❷ さらに正の方向へ3動く。
したがって，動いた結果は[mathjax] \(+8\)となる。
⑵ [mathjax]\((-5)+(-3)\)
❶ 0から負の方向へ5動く。
❷ さらに負の方向へ3動く。
したがって，動いた結果は[mathjax] \(-8\)となる。
問 ２ 数直線を使って，次の計算をしなさい。
⑴ [mathjax]\((+3)+(+4)\)
⑵ [mathjax]\((-2)+(-6)\)
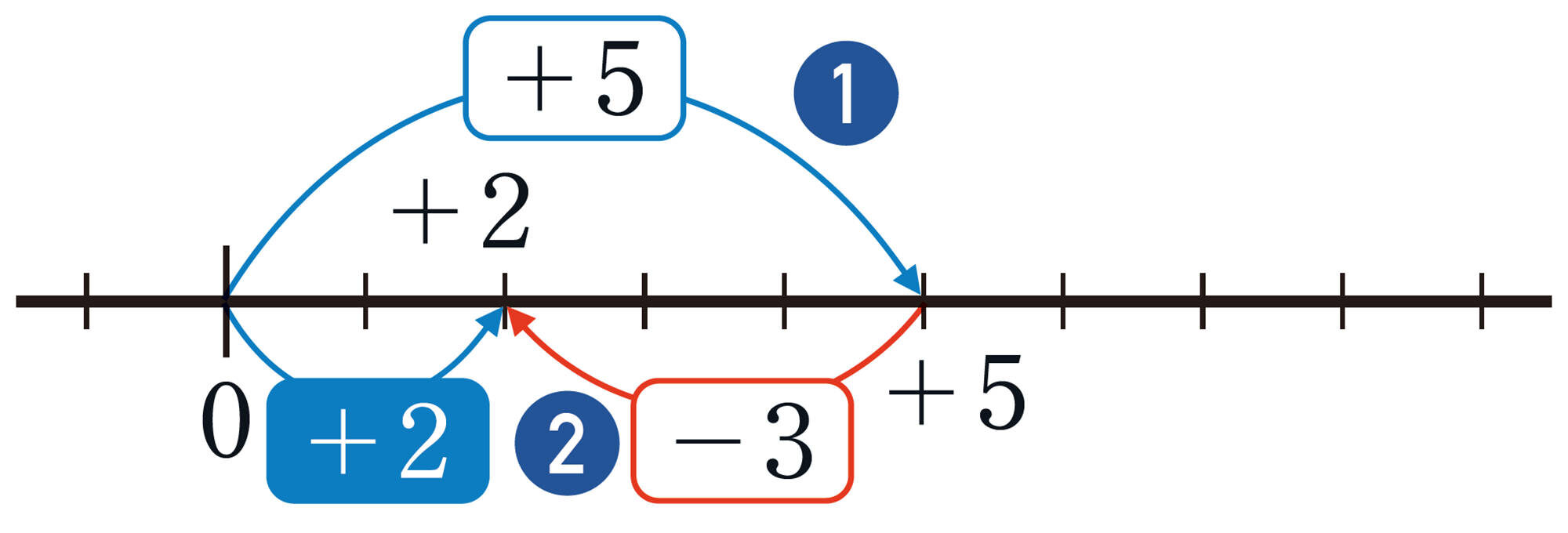
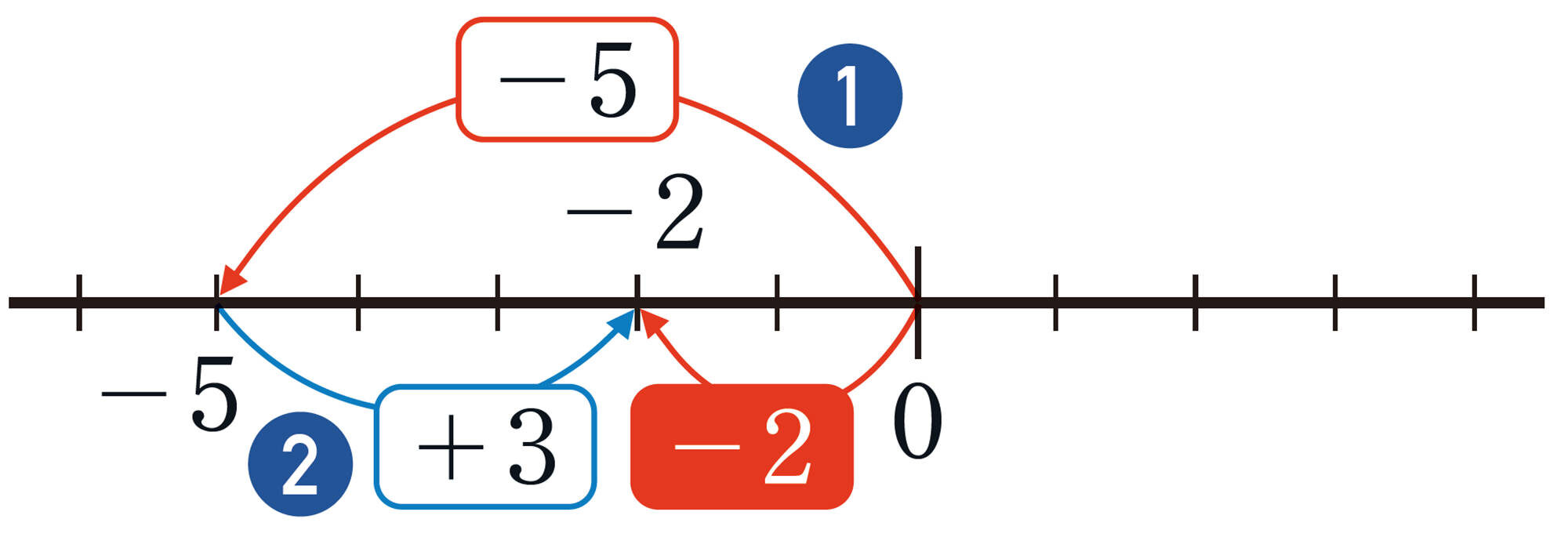
例２ 異符号の2数のたし算
⑴ [mathjax]\((+5)+(-3)\)
❶ 0から正の方向へ5動く。
❷ さらに負の方向へ3動く。
したがって，動いた結果は[mathjax] \(+2\)となる。
⑵ [mathjax]\((-5)+(+3)\)
❶ 0から負の方向へ5動く。
❷ さらに正の方向へ3動く。
したがって，動いた結果は[mathjax] \(-2\)となる。
<1年p.22>
問 ３ 数直線を使って，次の計算をしなさい。
⑴ [mathjax]\((+2)+(-6)\)
⑵ [mathjax]\((-2)+(+7)\)
たし算のことを 加法 という。その結果が和である。
符号と絶対値に着目した加法
Q Question
前ページの例1，例2で調べた同符号の2数の和と異符号の2数の和で，符号と絶対値について，気づいたことを話し合ってみましょう。
[mathjax]\((+5)+(+3)=+8 \)
[mathjax]\((-5)+(-3)=-8\)
[mathjax]\((+5)+(-3)=+2\)
[mathjax]\((-5)+(+3)=-2\)
正の数どうしの和と負の数どうしの和を比べてみよう。
符号がちがう2数のときは，どうなっているかな。
見方・考え方
符号と絶対値に着目すると，どんなきまりを見つけられるかな。
例 ３ 同符号の2数の和
⑴
⑵
例 ４ 異符号の2数の和
⑴
⑵
問 ４ 次の計算をしなさい。
⑴ [mathjax]\((+4)+(+13)\)
⑵ [mathjax]\((-8)+(-16)\)
⑶ [mathjax]\((-7)+(+8)\)
⑷ [mathjax]\((+14)+(-19)\)
問 ５ +3と-3の和を求めなさい。
<1年p.23>
正の数，負の数の加法について，次のようにまとめることができる。
正の数，負の数の加法
また，異符号で絶対値の等しい2数の和は，0である。
[mathjax]\((+3)+0=+3\)のように，ある数に0を加えても，和はもとの数に等しい。
また，[mathjax]\(0+(-2)=-2\)のように，0にある数を加えても，和は加えた数に等しい。
問 ６ 次の計算をしなさい。
⑴ [mathjax]\((+9)+(+5)\)
⑵ [mathjax]\((-5)+(-7)\)
⑶ [mathjax]\((+8)+(-3)\)
⑷ [mathjax]\((-16)+(+25)\)
⑸ [mathjax]\((-21)+(+21)\)
⑹ [mathjax]\(0+(-37)\)
小数や分数の加法
例 ５
⑴
⑵
整数の加法と同じように考えればいいね。
問 ７ 次の計算をしなさい。
⑴ [mathjax]\((+0.3)+(+1.2)\)
⑵ [mathjax]\((-0.7)+(+0.5)\)
⑶ [mathjax]\((+1.4)+(-0.9)\)
⑷ [mathjax] \(\require{physics}\left(-\dfrac{3}{5}\right) +\require{physics}\left(+\dfrac{4}{5}\right)\)
⑸ [mathjax] \(\require{physics}\left(-\dfrac{1}{2}\right)+\require{physics}\left(-\dfrac{3}{4}\right)\)
⑹ [mathjax] \(\require{physics}\left(+\dfrac{1}{4}\right) + \require{physics}\left(-\dfrac{5}{6}\right)\)
やってみよう
計算力を高めよう1-1
P.34
<1年p.24>
加法の交換法則・結合法則
Q Question
次の正の数，負の数の加法をして，それぞれ㋐，㋑の結果を比べてみましょう。どんなことがわかるでしょうか。
⑴ ㋐ [mathjax]\((+5)+(-7)\)
㋑ [mathjax]\((-7)+(+5)\)
⑵ ㋐ [mathjax]\(\{(-3)+(+6)\}+(-4)\)
㋑ [mathjax]\((-3)+\{(+6)+(-4)\}\)
ふりかえり
たされる数とたす数を入れかえても，和は変わらない。
[mathjax]\(\square + \triangle =\triangle +\square\)
3つの数をたすとき，たす順序を変えても，和は変わらない。
見方・考え方
負の数をふくむ加法も，小学校のときと同じように計算のきまりが成り立つかな。
小学校では，たす順序を変えても答えは変わらなかったね。
負の数があっても，答えは変わらないのかな。
注意 かっこを2重にしたいとき，記号[mathjax]\(\{\quad\}\)を使うことがある。
正の数，負の数の加法でも，次のことが成り立つ。
加法の交換法則 [mathjax]\(a+b=b+a\)
加法の結合法則 [mathjax]\((a+b)+c=a+(b+c)\)
加法では，交換法則や結合法則を使って，数の順序や組み合わせを変えて計算することができる。
文字には，正の数，負の数や0など，どんな数でもあてはめられるね。
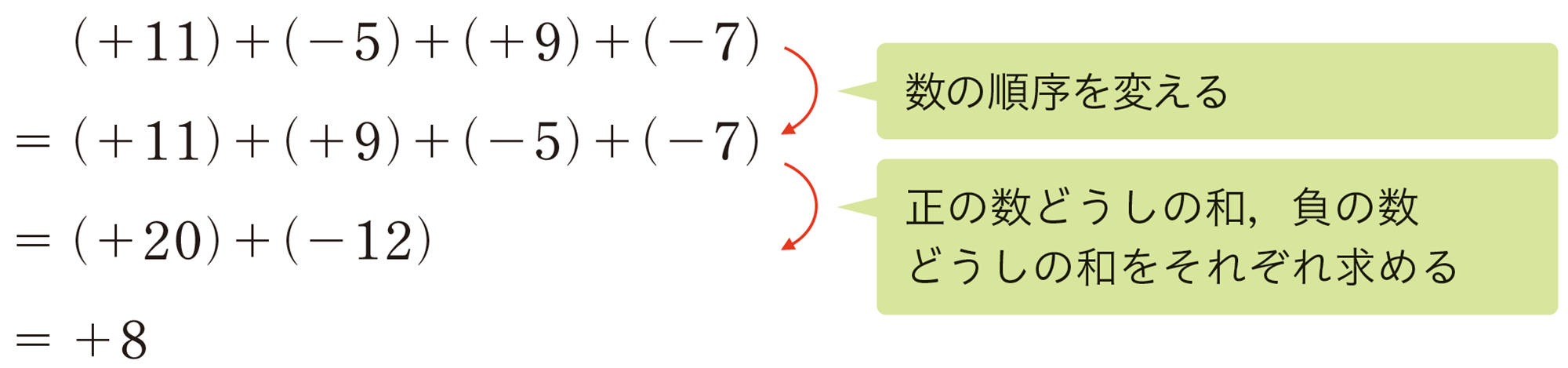
例 ６
数の順序を変える
正の数どうしの和，負の数どうしの和をそれぞれ求める
問 ８ 計算しやすい方法を考えて，次の計算をしなさい。
⑴ [mathjax]\((-12)+(+7)+(-6)+(+3)\)
⑵ [mathjax]\((+19)+(-5)+(-28)+(-14)\)
どんなことがわかったかな
正の数，負の数の加法は，符号や絶対値に着目して計算することができます。また，加法の交換法則・結合法則が成り立ちます。
次の課題へ！
正の数，負の数のひき算も，加法と同じようにできるのかな？
P.25
