<1年p.9>
１章 Chapter 1 正の数・負の数
１節 正の数・負の数
２節 加法・減法
３節 乗法・除法
４節 数の集合
[mathjax]\(20-5\)だから，那覇市の明日の最高気温は15℃だね。
札幌市の明日の最高気温は，[mathjax]\(-5-3\)ということかな。計算できないよ。
？ 0より小さい数は計算できるの？
<1年p.10>
1節 正の数・負の数
「[mathjax]\(-\)」のついた数ってなんだろう？
【１】 身のまわりから「[mathjax]\(-\)」のついた数を探してみましょう。
ほかにも「[mathjax]\(-\)」のついた数はあるかな。
<1年p.11>
【2】 「[mathjax]\(-\)」のついた気温について考えてみましょう。
気温は「[mathjax]\(-\)」のついた数を使うけど，「[mathjax]\(-\)」って何だろう。
前日差は，前の日の気温とのちがいを表しているね。
札幌の最高気温の「[mathjax]\(-\)」と前日差の「[mathjax]\(-\)」は，同じことを表しているのかな。
最高気温がもっとも高いところと，もっとも低いところはどこかな。
次の課題へ！
｢[mathjax]\(-\)｣のついた数は，どんな数なのかな？
P.12
<1年p.12>
１ 符号のついた数
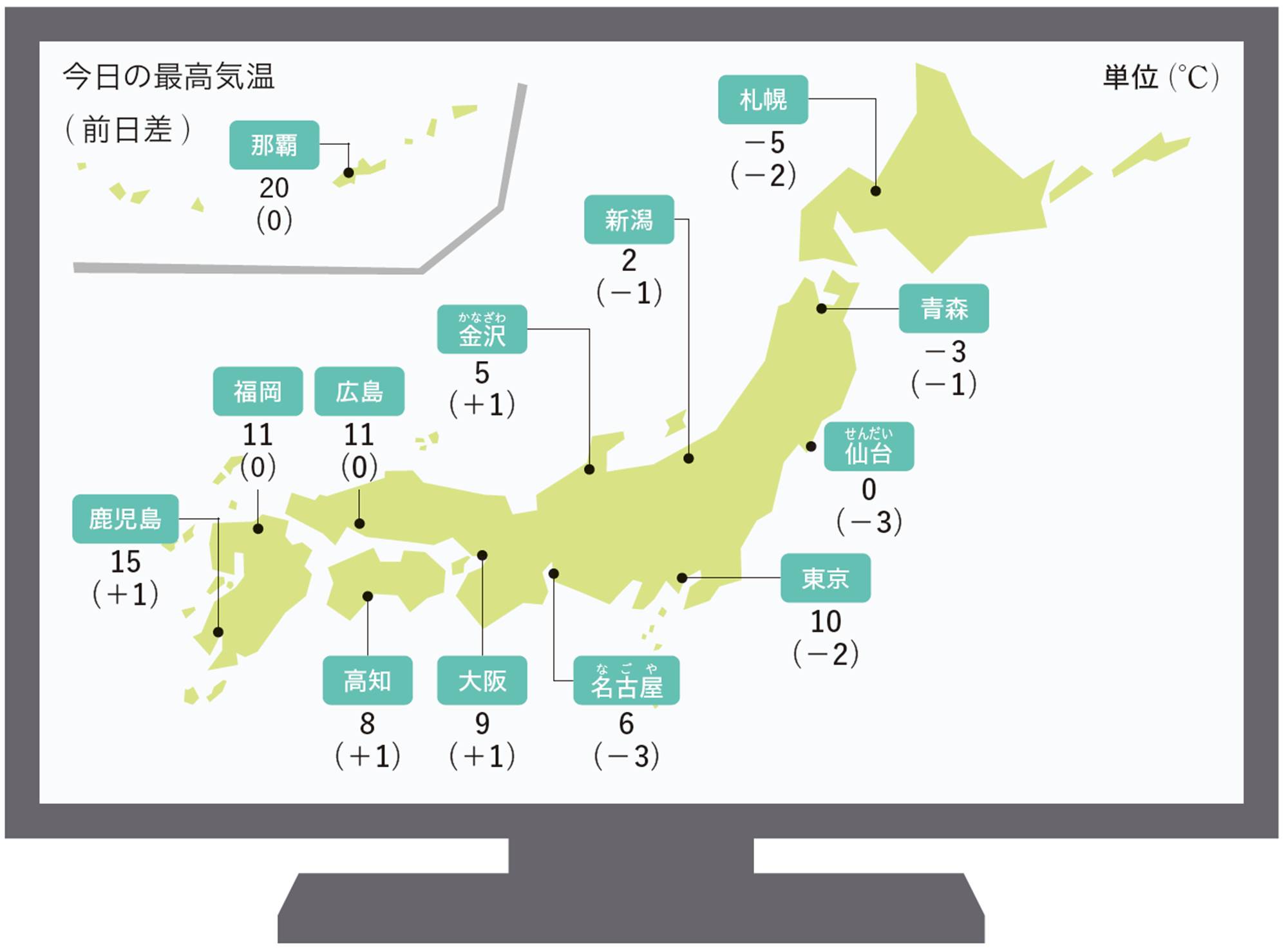
0を基準とした数量
Q Question
右の2つの温度計は，ある日の午前6時における新潟と鹿児島の気温を示しています。
それぞれ何℃を示しているでしょうか。
また，「[mathjax]\(-\)」のついた気温はどのようなことを表しているか考えてみましょう。
0℃より低い気温に「[mathjax]\(-\)」がついているね。
0より小さいということかな。
見方・考え方 どこに着目して考えればいいかな。
目標 ▷ 「[mathjax]\(-\)」のついた数の意味を考えよう。
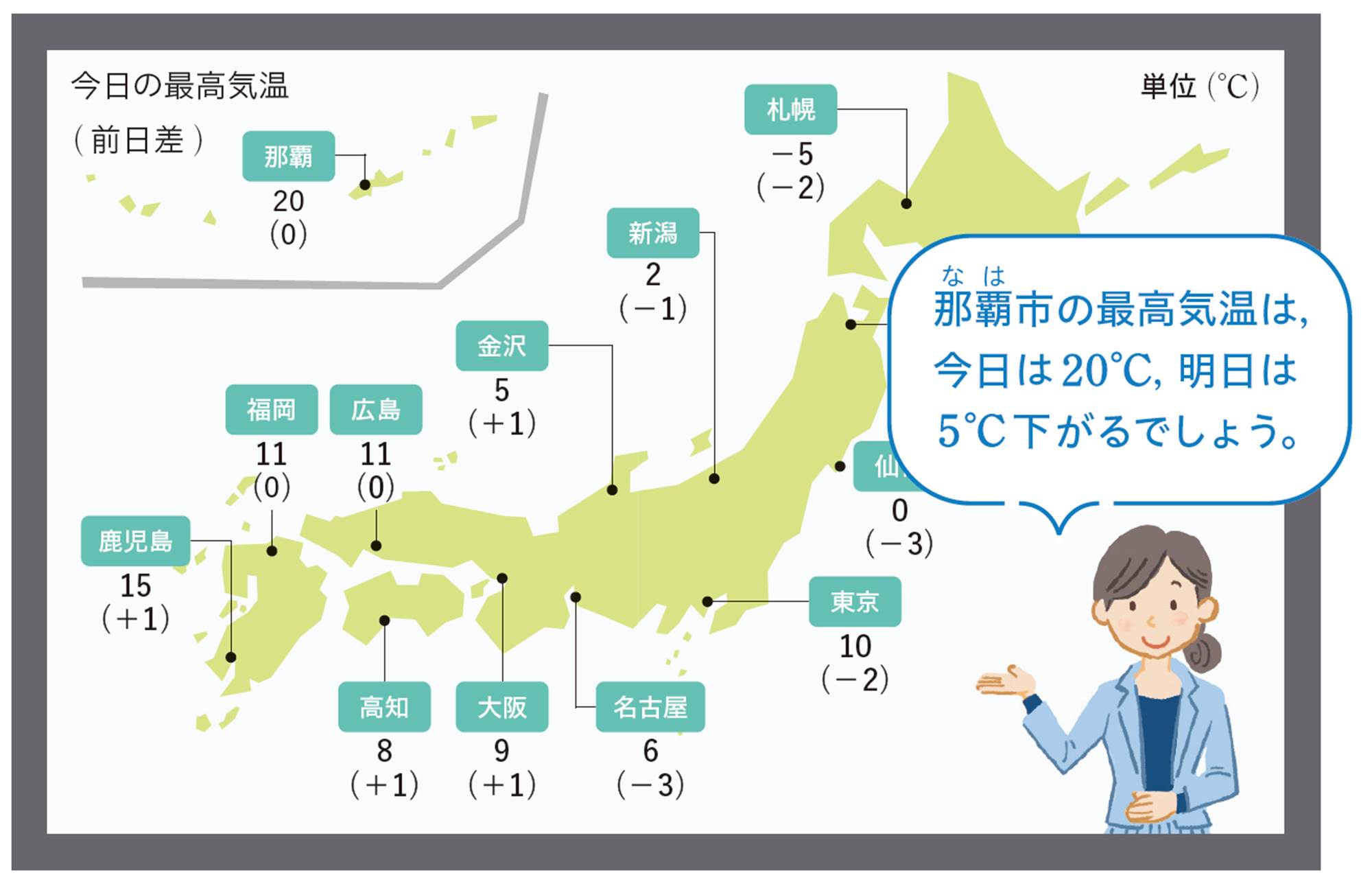
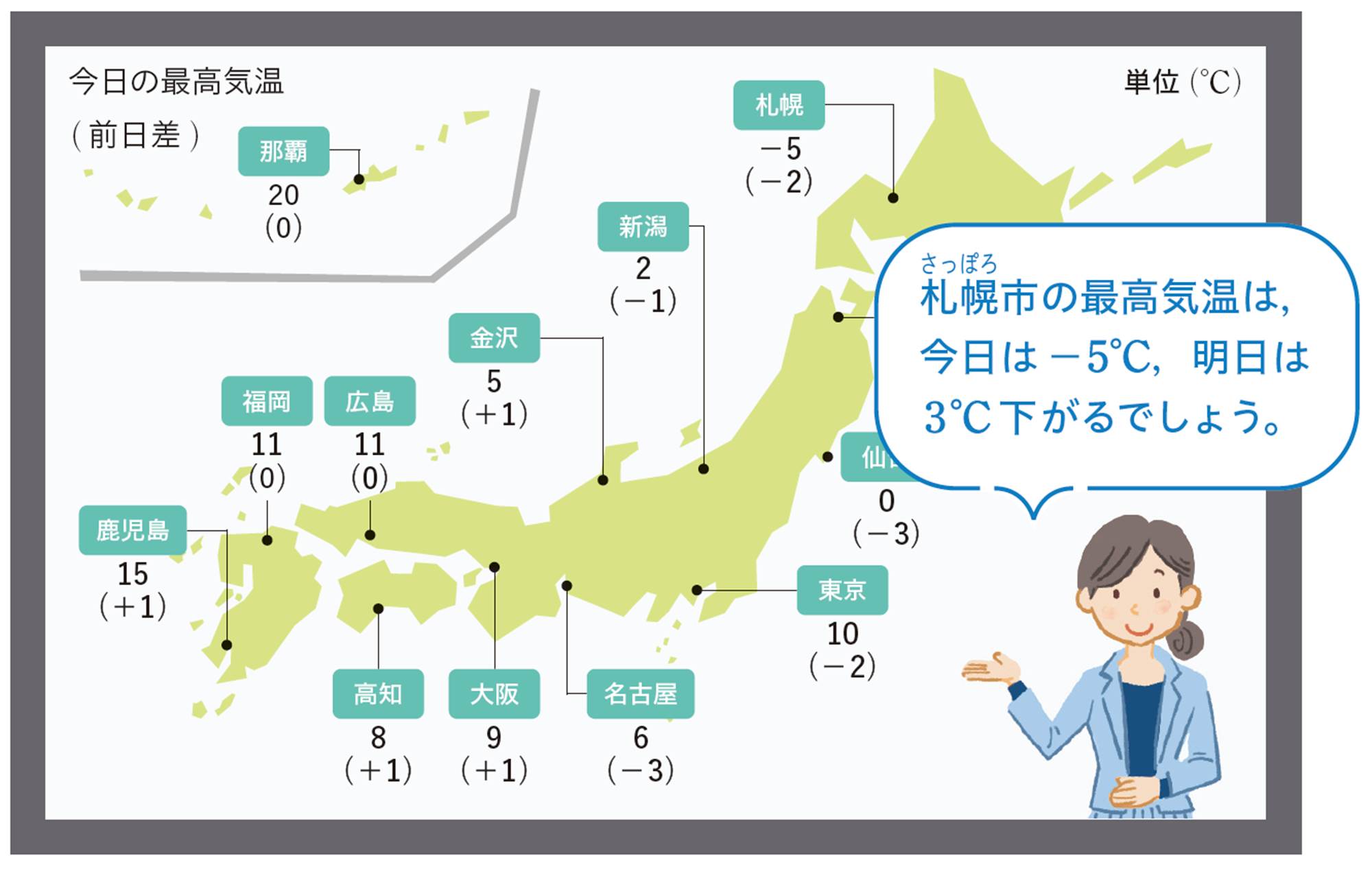
0℃より2℃低い温度は，[mathjax]\(-\)を使って[mathjax]\(-2\)℃と表し，「マイナス2℃」 と読む。これに対して，0℃より8℃高い温度は，[mathjax]\(+\)を使って[mathjax]\(+8\)℃と表すことがあり，これを 「プラス8℃」 と読む。
[mathjax]\(+\)，[mathjax]\(-\)をこのように使うとき，[mathjax]\(+\)を 正の符号 ，[mathjax]\(-\)を 負の符号 という。
問 １ 次の温度を，正の符号，負の符号を使って表しなさい。
⑴ 0 ℃より[mathjax]\(6.5\) ℃高い温度
⑵ 0 ℃より10 ℃低い温度
水がこおるときの温度を基準0℃とすると，0℃より高い温度は正の符号，低い温度は負の符号を使って表すことができる。
このように，反対の性質をもつ数量では，基準を決めてその基準を0とすることで，その一方を正の符号を使って表すと，他方は負の符号を使って表すことができる。
<1年p.13>
「[mathjax]\(-\)」のついたいろいろな数量
Q Question
富士山の標高は3776m，伊豆・小笠原海溝の最大水深は9780mです。
これらの値を次の図のように表すとき，正の符号，負の符号を使うと，それぞれどのように表すことができるでしょうか。
標高と水深は，反対方向の長さだね。
標高と水深の境目はどこかな。
見方・考え方
どこを基準0mとして考えているかな。
問 １ A 地点を基準0km として，「A から東へ6km」の地点を[mathjax]\(+6\) km と表すとき，「A から西へ4km」の地点は[mathjax]\(-4\)km と表すことができる。
問 ２ 例1で，[mathjax]\(-7\)km，[mathjax]\(+2.5\)km は，それぞれどの地点を表していますか。上の図に矢印↑で示しなさい。また，その地点をことばで表現しなさい。
問 ３ 次の数量を，正の符号，負の符号を使って表しなさい。
⑴「400円の利益」を[mathjax]\(+400\)円と表すとき，「500円の損失」
⑵「いまから20分前」を[mathjax]\(-20\)分と表すとき，「いまから30分後」
問 ４ 陸上競技で100m 競走などの記録を示す場合，秒速[mathjax]\(2.0\)m の追い風があったときは，「[mathjax]\(+2.0\)m/s」と表示されます。「[mathjax]\(-2.3\)m/s」と表示されたときは，どんなことを示していますか。
<1年p.14>
例２ 次の表は，大和さんの5回の漢字テストの点数です。大和さんの目標の点数は7点です。目標の点数を基準として，テストの点数が目標の点数より高いときは正の符号，低いときは負の符号を使って表す。
1回目のテストの点数は，目標の点数より1点低いので，[mathjax]\(-1\)点と表される。
問 ５ 例2で，2回目から5回目の点数を，目標の点数を基準として表しなさい。
正の数・負の数
例３ 0より大きい数や小さい数を，正の符号，負の符号を使って次のように表す。
⑴ 0より8大きい数 [mathjax]\(+8\)
⑵ 0より4小さい数 [mathjax]\(-4\)
[mathjax]\(+8\)， [mathjax]\(+10\)のように，0より大きい数を 正の数 といい，[mathjax]\(-4\)，[mathjax]\(-9\)のように，0より小さい数を 負の数 という。0は，正の数でも負の数でもない数である。
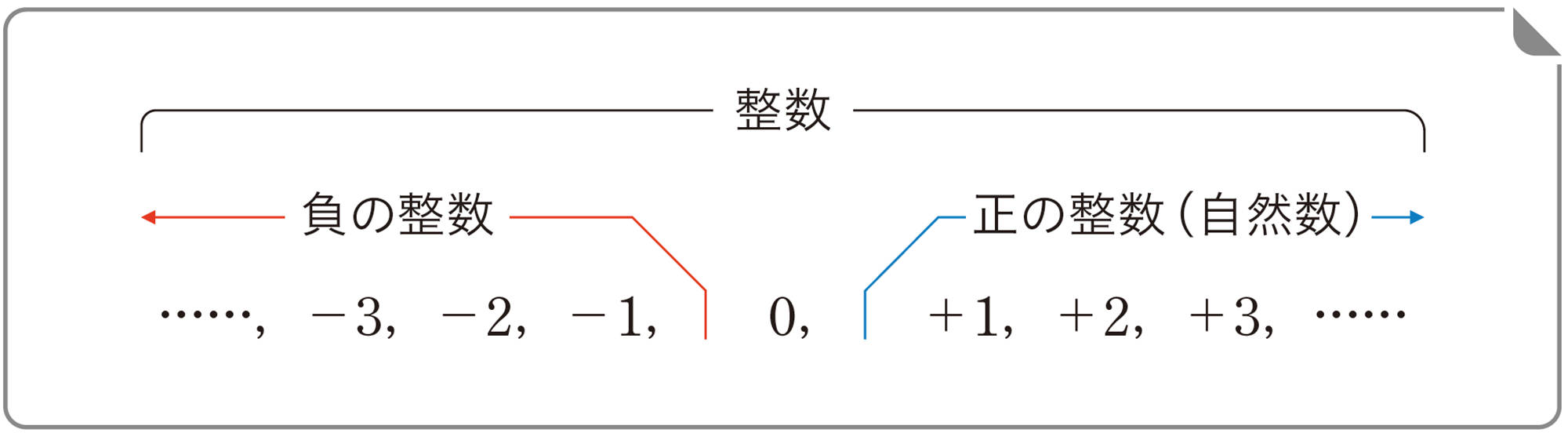
小学校では，正の数と0について学んできたが，中学校では，数といえば負の数もふくめて考える。つまり，これからは整数といえば，正の整数，0，負の整数のことをいう。また，正の整数を 自然数 ともいう。
問 ６ 次の数は，正の数，負の数のどちらですか。また，0よりどれだけ大きいか小さいかをいいなさい。
⑴ [mathjax]\(-6\)
⑵ [mathjax]\(+3\)
⑶ [mathjax]\(+1.2\)
⑷ [mathjax] \( -\dfrac{2}{5}\)
⑸ [mathjax]\(-0.1\)
⑹ [mathjax] \(+\dfrac{5}{3}\)
小数や分数にも，正の数，負の数があるね。
どんなことがわかったかな
基準の0を決めると，反対方向の数量を正の数，負の数を使って表すことができます。
次の課題へ！
正の数，負の数の大小は，小学校で数の大小を比べたときと同じように比べられるのかな？
P.15
